こんにちは!ぼりたそです!
今回は、多目的最適化(Multi-objective Optimization)についてわかりやすく解説していきます。
これまで当ブログでは、ベイズ最適化など「単一の目的関数を最適化する方法(単目的最適化)」を紹介してきました。
しかし実際の現場では、「精度を上げたいけれどコストは抑えたい」「反応速度を早めたいが安全性も重視したい」など、複数の目標を同時に満たしたい場面が多く存在します。
そんなときに役立つのが、多目的最適化です!
この記事では以下のポイントで整理しています。
- 多目的最適化とは?
- パレート解とパレートフロント
- 最適化手法
それでは順に解説していきます。
多目的最適化とは?
多目的最適化とは、複数の評価指標(目的変数)を同時に最適化するための手法です。
一方で、目的が1つの場合は「単目的最適化」と呼ばれます。
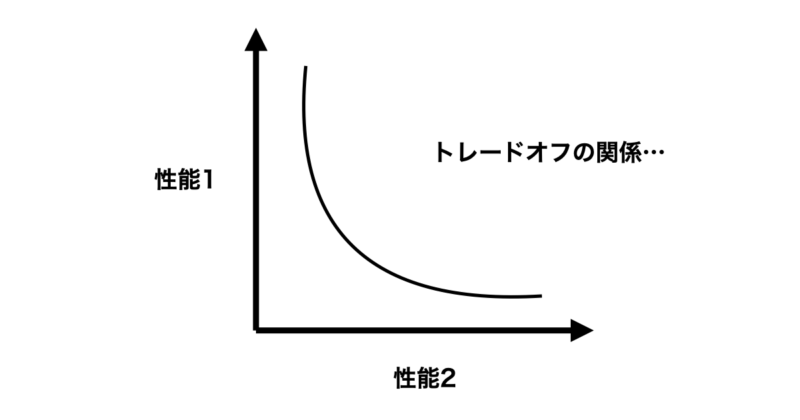
例えば、ある会社で新製品を立ち上げようとした時に性能1を上げたいけれど、逆にその分、性能2下がってしまうという問題があったとします。
このように、一方を改善するともう一方が悪化するような関係は「トレードオフ」と呼ばれます。
このバランスを取るのが多目的最適化の目的です。
パレート解とパレートフロント
多目的最適化では、「どの解が最も良い」と一概に言い切れないことがよくあります。
このような場合、「他の解に完全には劣らない解」をパレート解と呼びます。
簡単に言えば、完全上位互換の解を持たない解ということになります。
たとえば、以下のような3つの解(製品)を考えてみます。
- 点A:性能1が80点、性能2が70点
- 点B:性能1が90点、性能2が80点(← 点Aより全体的に優れている)
- 点C:性能1が65点、性能2が100点(← 点Aより 性能1では劣っているが、性能2では優れている)
点Bは点Aを完全に上回っているため点Bをパレート解、点Aを劣解と呼びます。
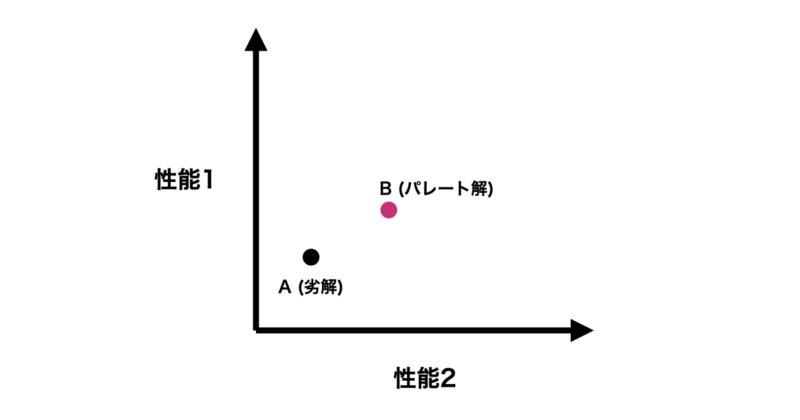
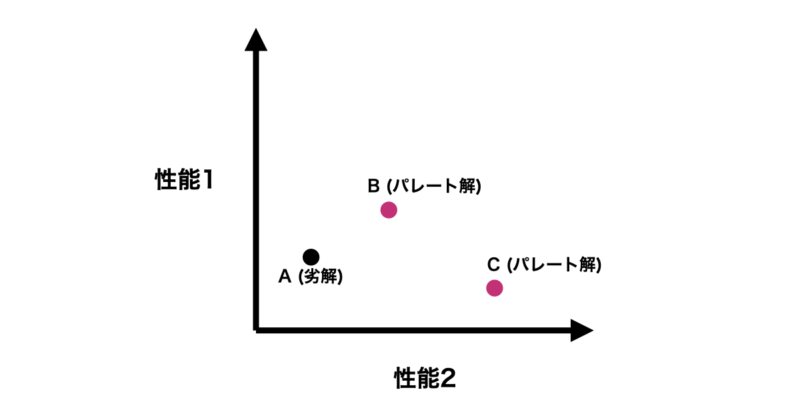
さらに点Cの場合、点A, Bに対して性能1では劣りますが、性能2では優れています。よって点Cは完全な上位互換を持たないため、点Bと同じくパレート解になります。
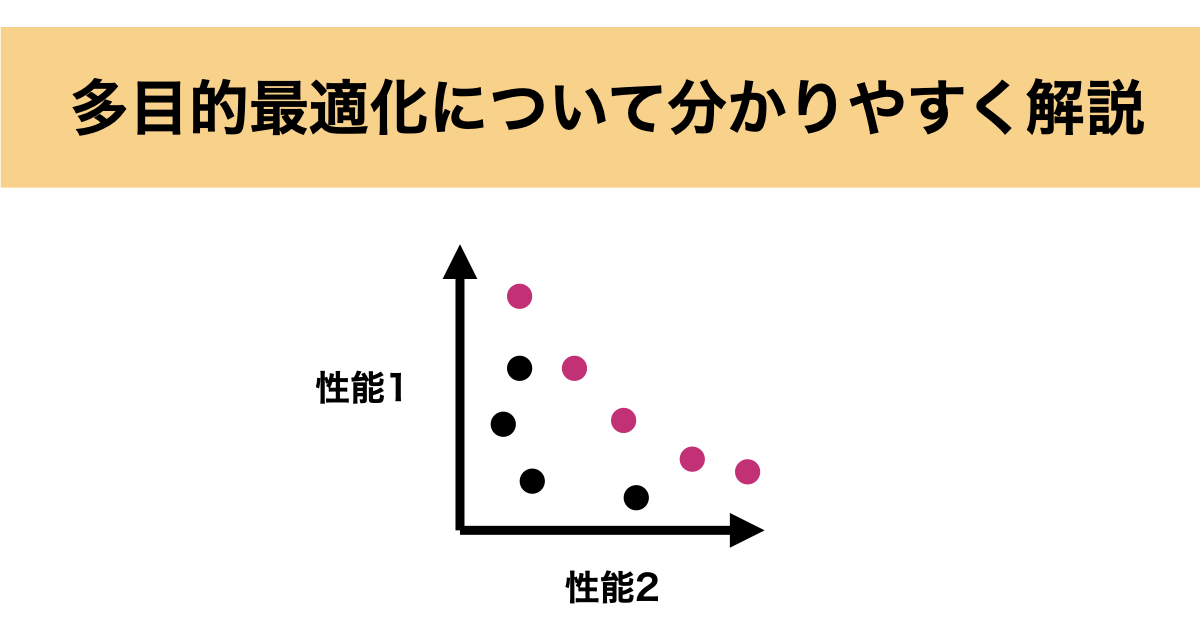
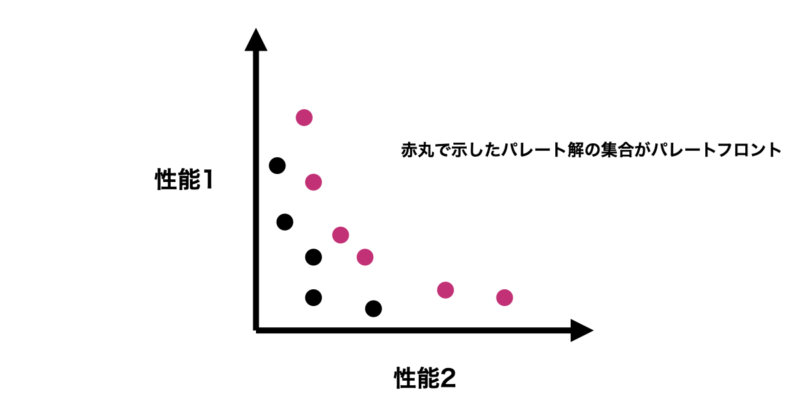
さらに検討を進め、下のようなプロットが描けたとします。この時、パレート解は赤丸で示したプロットとなり、このパレート解の集合をパレートフロントと呼びます。
最適化手法
では、実際に多目的最適化の手法についてどのようなものが存在するかご説明します。
多目的最適化手法としては大きく二つ挙げられます。
- スカラー化によって1つの解を導く
- パレートフロントを推定する
以下、順に説明していきます。
スカラー化によって1つの解を導く
複数の目的変数を重み付きで1つの指標(スカラー値)に変換し、単目的最適化を実行する方法です。
これを「スカラー化法(Scalarization)」と呼びます。
数式で表すと以下のようになります:
$$ \text{minimize or maximize} \quad F(\mathbf{x}) = \sum_{i=1}^{m} w_i \cdot f_i(\mathbf{x}) $$
ここで
- $ f_i(\mathbf{x}) $:目的関数(評価指標)
- $ w_i $:目的変数ごとの重み
この手法のメリットとしてはそれぞれの目的変数の重みを自由に設定することで、自分の目指したいバランスの取れた最適化を実行することができます。
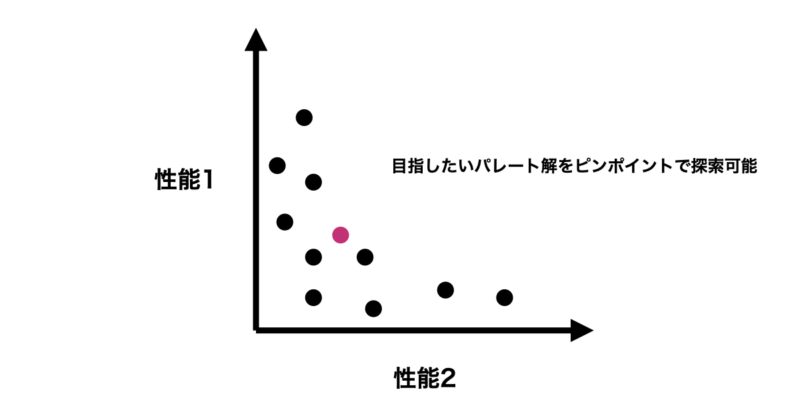
一方でパレート解の一部しか得られないという制約があります。
パレートフロントを推定する
こちらは「全てのパレート解を求めることを目的とした手法」です。
そのためには、どの解がどれだけパレートフロントを広げるかという観点が重要になります。
ここで出てくる概念が「パレート超体積(Hypervolume)」です。
パレート超体積とは複数のパレート解によって囲まれた空間(体積・面積)を指します。
最大化したい目的変数が二つの最適化を例に挙げると下のように赤丸で示したパレート解に囲まれた青の領域がパレート超体積になります。
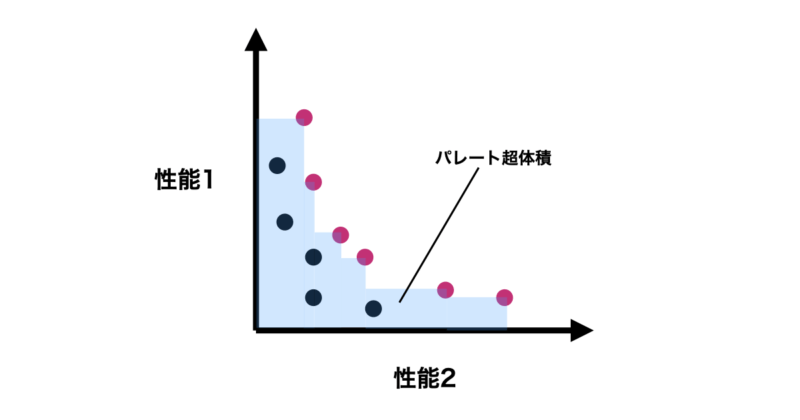
パレートフロントを推定する場合は現状のパレートフロントを改善するような解を見つけるように探索する必要があります。
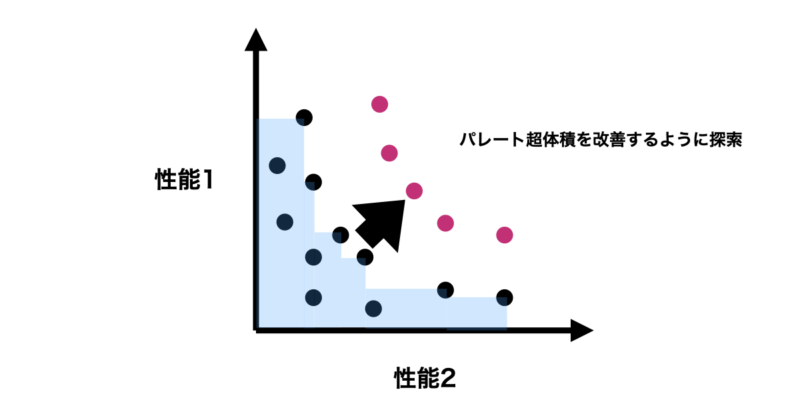
ではどのようにパレートフロントを改善するかというと、パレート超体積の改善値をスコアリングするような獲得関数を使用します。
獲得関数とは最適化問題に対して事後分布からスコアリングして次の候補点を決める指標になります。
獲得関数については以前記事でまとめたので興味があれば以下の記事をご参考下さい。
多目的最適化でよく使用される獲得関数は以下の二つです。
- EHVI(Expected Hypervolume Improvement)
パレート超体積の増分を期待値として評価する獲得関数です。要するにパレートフロントをどれだけ改善できるかを評価しているということです。
- HVPI(Hypervolume-based Probability of Improvement)
パレート超体積が増加する確率を評価する獲得関数です。EHVIは改善期待値を計算しているので少し評価方法が異なっています。
どちらも、「パレートフロントをどれだけ改善できそうか」をスコア化して、次の評価点を選ぶために使われます。
実装する場合はPtyhonのライブラリであるGPyOptやOptunaなどを使用して多目的最適化を実行します。
多目的最適化の実装については今後まとめて記事にする予定なので、お待ちいただければと思います。
終わりに
以上が多目的最適化についての説明になります。実際に最適化問題を解く際はほとんどの場合が多目的最適化になるかと思います。実際に多目的最適化を実行することはなくとも、どのようなアルゴリズムで動いているのかしっかりと理解したいですね。