こんにちは!ぼりたそです!
今回は最適化手法の一つである遺伝的アルゴリズムについてわかりやすく解説していきます。
この記事は以下のポイントでまとめています。
- 遺伝的アルゴリズムとは?
- 遺伝的アルゴリズムの流れ
- Pythonでの実装
また、CSVを入力するだけで遺伝的アルゴリズムを実行するPythonコードも紹介しているので、ご興味ある方は以下の記事を参照ください。
それでは順に解説していきます。
遺伝的アルゴリズムとは?
まずは遺伝的アルゴリズムについて簡単に説明していきます。
遺伝的アルゴリズム(Genetic Algorithm, GA)は、生物の進化に着想を得た最適化手法で、人工知能や機械学習、組み合わせ最適化問題などで広く利用されています。
GAは主に「自然選択」「遺伝子操作」を模倣して解を進化させることで、最適解やそれに近い解を探索することが可能です。
例えば、以下のような問題を解決する場合にGAが役立ちます。
- ナップサック問題:
複数のアイテムを限られた容量のナップサックに詰める問題で、最大の価値を得る組み合わせを探します。
- スケジューリング問題:
例えば、ジョブをマシンに効率よく割り当てる問題。GAを使用することで複数の制約条件を満たしつつ、最適なスケジュールを見つけることができます。
- 迷路解決:
GAを使って、迷路を効率的に解くための最適なパスを見つけることができます。
- フィーチャー選択:
大量のデータから重要な特徴量を選び出す問題にGAが使われることがあります。
上記の問題で遺伝的アルゴリズムが使用される理由は、GAが広範な探索空間を効率的に探索し、複数の局所最適解に対してグローバル最適解を見つけるのに適しているためです。
さらに、GAは並列計算に向いており、複数の解を同時に探索することで、高度に複雑な問題にも対応できる強力なツールとなります。
遺伝的アルゴリズムの流れ
次に遺伝的アルゴリズム(GA)の流れについて説明していきます。
GAは主に以下のステップを繰り返すことで最適解に近づいていきます。
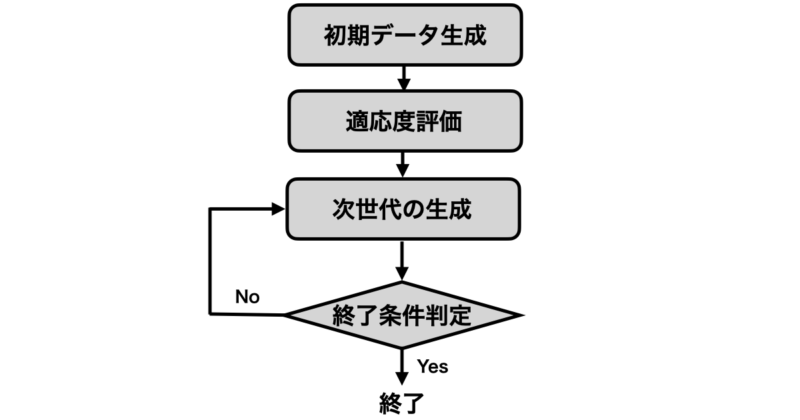

- 第一世代の生成
ランダムに初期の解候補(個体)を生成します。
- 適応度の評価
各個体に対して評価関数を用いて適応度を計算します。
- 次世代の生成
初期集団から次世代を生成し、再度適応度の評価を行います。
- 終了条件の判定
世代交代のプロセスを繰り返し、事前に設定した条件(例えば一定の世代数に達する、あるいは適応度が十分高い解が見つかるなど)を満たすと終了します。
以下、1〜3のプロセスについて説明していきます。
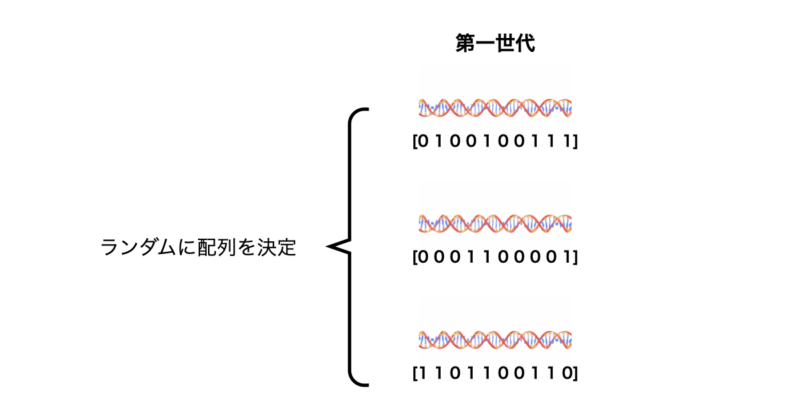
第一世代の生成
まずは第一世代の生成について説明します。
第一世代はGAの探索プロセスの出発点です。多様で質の高い個体を生成することで、アルゴリズムは広範な探索を行い、優れた解に到達する可能性が高まります。
逆に、個体が偏っていたり、探索空間の一部しかカバーしていない場合、最適解を見逃すリスクが増加します。
では、どのようにして第一世代を生み出せばいいのでしょうか?
一般的には以下の手法を組み合わせて生成することが多いです。
ランダム生成
最も一般的な方法で、探索空間全体からランダムに個体を生成します。
特徴として以下の点が挙げられます。
- 実装が簡単で、多くの問題に適用可能。
- 広範な探索空間をカバーできる可能性が高い。

データがバイナリビット(0 or 1)であれば0と1をランダムに設定すればよく、実数であれば規定した範囲内の実数を生成すればランダム生成することができます。
ヒューリスティック生成
分野固有の知識や勘を用いて、より良い初期個体を生成する手法です。
ヒューリスティック生成は以下のような特徴が挙げられます。
- 初期集団の質が高く、収束が早まる可能性。
- 問題ごとにカスタマイズが必要。
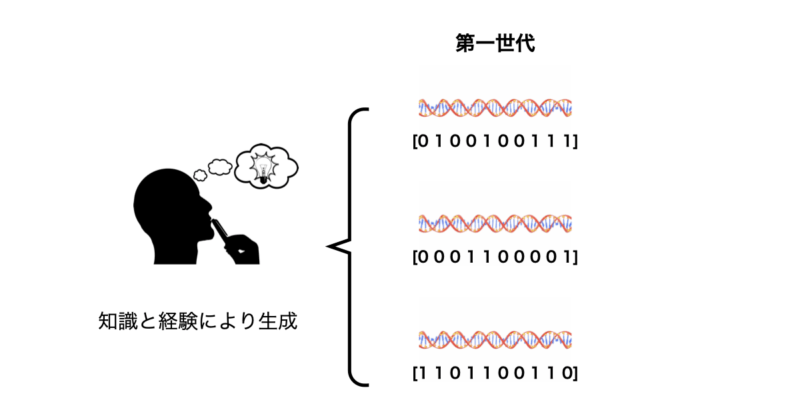

具体的には既知の良好な解や部分解を含める、特定のルールやパターンに基づいて遺伝子を配置するなどの手法をとることが多いです。
エリート生成
既存の良好な解を初期集団に含める方法です。
特徴としては以下の点が挙げられます。
- 優れた解が失われるリスクを減少。
- 初期集団の質を向上させる。
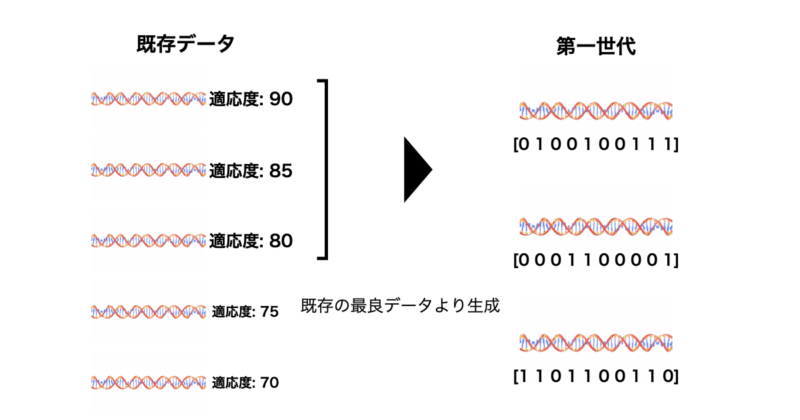

具体的には既存のデータセットや過去の最適解から個体を選択し、問題に応じてエリート個体を第一世代に追加する手法が取られます。
クラスタリング生成
探索空間をクラスタに分割し、各クラスタから均等に個体を生成します。
特徴としては以下の点が挙げられます。
- 初期集団の多様性を確保しやすい。
- 特定の領域に偏らない探索が可能。
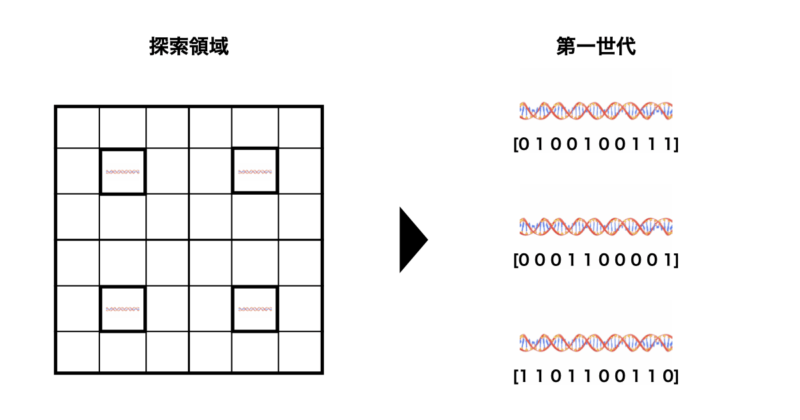

具体的には探索空間をクラスタリング手法(例: K-means)で分割し、各クラスタからランダムに個体を生成する手法が取られたりします。
次世代の生成
次に次世代の生成について説明していきます。
次世代の生成は、遺伝的アルゴリズム(GA)の進化プロセスにおいて中心的な役割を果たします。親世代からスタートし、各世代で適応度の高い個体を選択し、新しい個体を生成することで、より良い解に到達することを目指します。
次世代の生成は、選択(Selection)、交叉(Crossover)、突然変異(Mutation)の3つの主要な手法から構成されます。
以下、この3つの手法について説明していきます。
選択(Selection)
まずは選択について説明していきます。
選択(Selection)は、親世代の遺伝子をそのまま次世代へコピーする手法になります。言わばクローンのようなものと考えていただけるとわかりやすいかと思います。
この選択では、適応度の高い個体が選ばれる確率が高くなるように設計されており、進化の過程で優れた解を次の世代に伝え、探索効率を高めることができます。
しかし、適応度の高い個体を選択すると言っても、その個体を決める方法は様々です。
以下に選択の一般的な手法をご紹介します。それぞれ特徴があり、メリット、デメリットが存在します。
ルーレット選択
まずはルーレット選択です。
以下に原理や具体的な手順、メリット&デメリットについて記載します。
原理
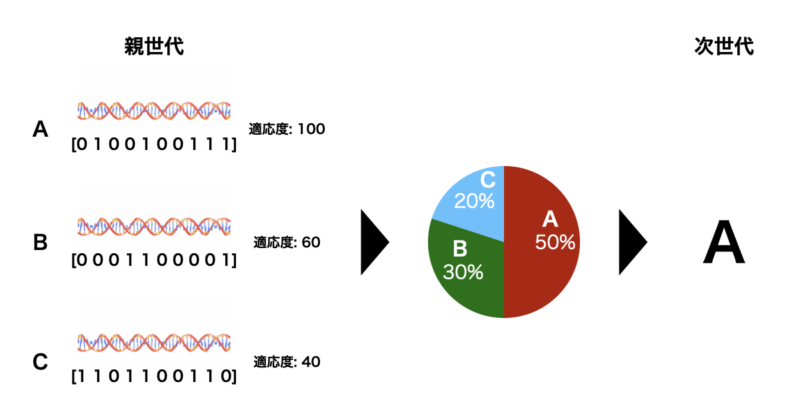
- 各個体の適応度に比例して選ばれる確率が決まる手法。
- 個体の適応度を円グラフのセグメントとして表現し、そのセグメントの大きさが選択確率を表します。適応度が高い個体ほど大きなセグメントを持ち、選ばれる可能性が高くなります。

手順
- 各個体の適応度を合計し、その合計値をもとに各個体の選択確率を計算。
- 0から1までのランダムな数を生成し、その値が該当するセグメントの個体を選びます。
メリット&デメリット
- メリット: 簡単に実装でき、適応度が高い個体が次世代に伝わりやすい。
- デメリット: 適応度の差が大きすぎる場合、偏りが生じて遺伝的多様性が失われるリスクがあります。
トーナメント選択
次にトーナメント選択です。
以下に原理、手順、メリット&デメリットを記載します。
原理
- 複数の個体をランダムに選んで「トーナメント」を行い、その中で最も適応度の高い個体を親として選択します。トーナメントのサイズが大きいほど、適応度の高い個体が選ばれる確率が高くなります。
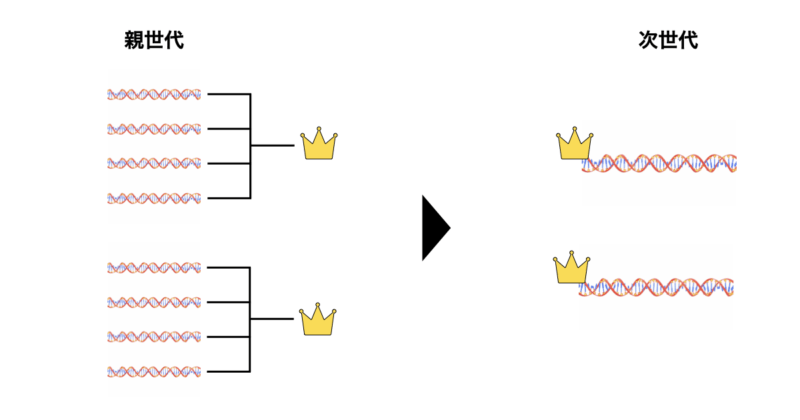

手順
- ランダムに指定された数の個体を選び、その中で最も適応度の高い個体を選びます。
- トーナメントを複数回行い、次世代に必要な親個体数が揃うまで繰り返します。
メリット&デメリット
- メリット: トーナメントサイズを調整することで、選択圧(適応度の高い個体が選ばれる確率の高さ)をコントロールできる。遺伝的多様性を保ちやすい。
- デメリット: トーナメントサイズが小さすぎると、ランダム性が強くなりすぎて、適応度の高い個体が選ばれにくくなる。
エリート選択
次にエリート選択についてです。
以下に原理、具体的な手順、メリット&デメリットについて記載します。
原理
- 現世代で最も適応度の高い個体をそのまま次世代に引き継ぐ方法です。これにより、最良の解が失われるリスクを回避します。
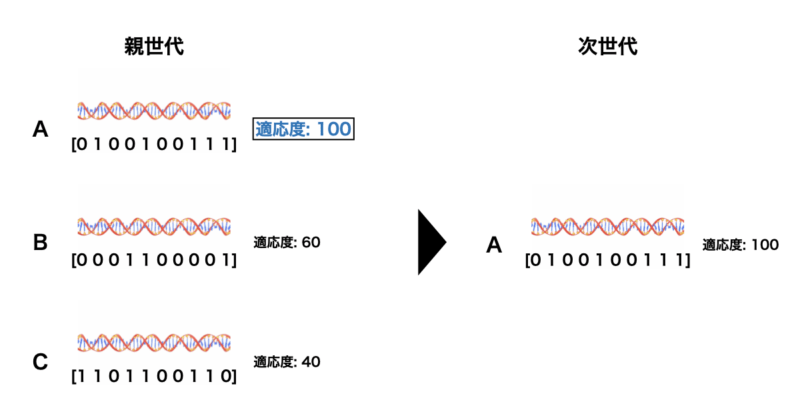

手順
- 現世代の個体の中で最も適応度の高い個体を選びます。
- この個体をそのまま次世代に移行させ、他の親個体の選択と新しい個体の生成を行います。
メリット&デメリット
- メリット: 最適解を保護できるため、アルゴリズムが良好な解を見失うことがない。
- デメリット: エリート個体が次世代に必ず残るため、遺伝的多様性が失われる可能性があります。
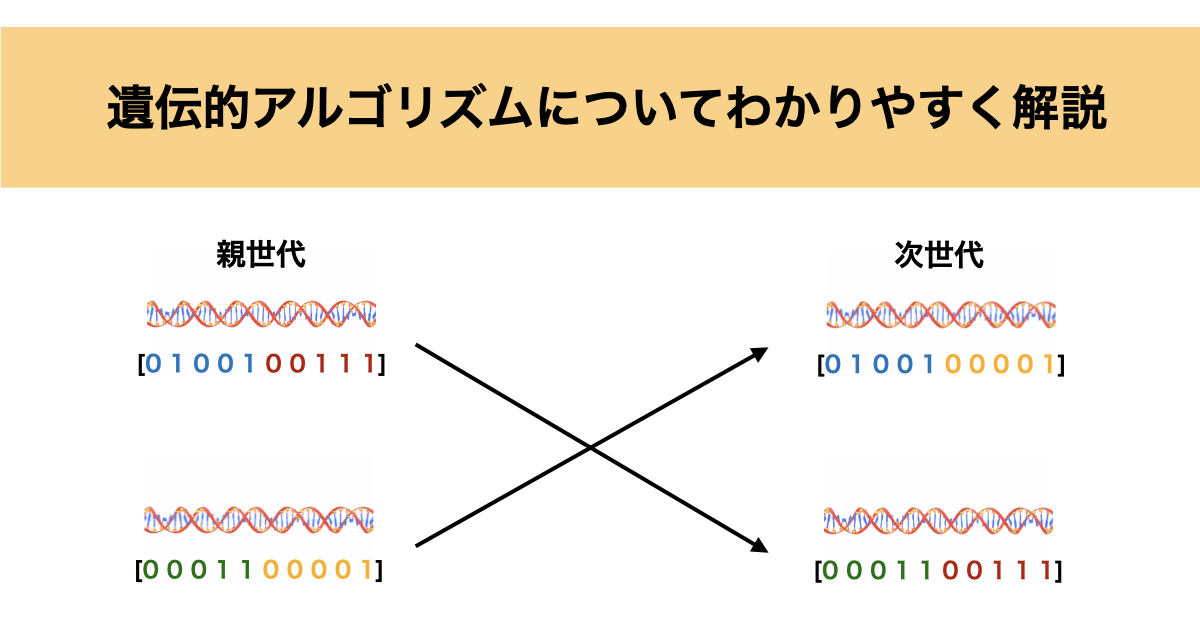
交叉(Crossover)
次の次世代生成の手法として交叉(Crossover)について説明していきます。
交叉(Crossover)は選択された親同士の遺伝子情報を組み合わせて新しい子供個体を生成するプロセスであり、自然界の一般的な交配を模した手法になっています。
交叉の主な目的は、親同士の優れた遺伝情報を組み合わせることで、次世代の個体群がより良い解を含む可能性を高めることです。
交叉によって得られる子供個体は、親の特徴を引き継ぎつつ、遺伝的多様性が向上するため、局所最適解に陥るリスクを減少させます。
しかし、親の遺伝子の組み合わせ方にもいくつか手法があり、以下に一般的に使用される手法についてご紹介します。
一点交叉
まずは一点交叉について説明していきます。
以下に原理、具体的な手順、メリット&デメリットについて記載します。
原理
- 一点交叉では、親個体の遺伝子列の中から1つの交叉点をランダムに選び、その交叉点で親個体の遺伝子を分割し、それぞれの遺伝子の一部を交換することで新しい子個体を生成します。
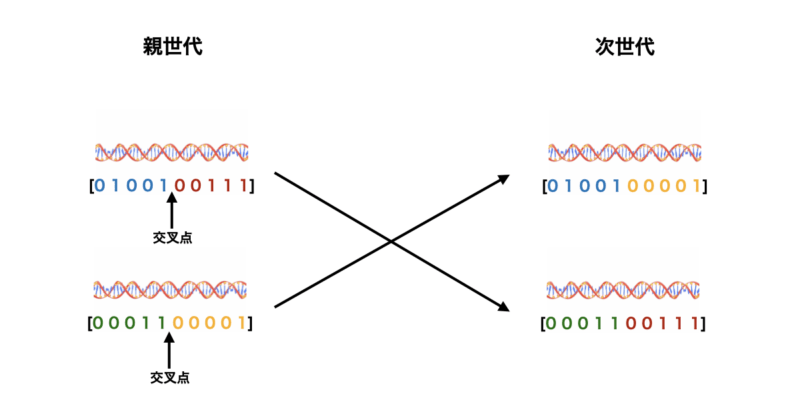

手順
- 親個体の遺伝子列を用意します(例: 親A =
11011、親B =00101)。 - ランダムに1つの交叉点を選びます(例: 交叉点が2番目の後)。
- 交叉点を境にして、親個体の前半と後半を入れ替えます(例: 子供A =
11001、子供B =00111)。
メリット&デメリット
- メリット: 親個体の一部を確実に引き継ぐため、遺伝子の良い部分が維持されやすい。
- デメリット: 特定の遺伝子が過剰に次世代に伝わりやすく、局所最適解に陥る可能性があります。
二点交叉
次に二点交叉について説明していきます。
以下に原理、具体的な手順、メリット&デメリットについて記載します。
原理
- 二点交叉では、親個体の遺伝子列から2つの交叉点をランダムに選び、その間の遺伝子を交換して新しい子個体を生成します。
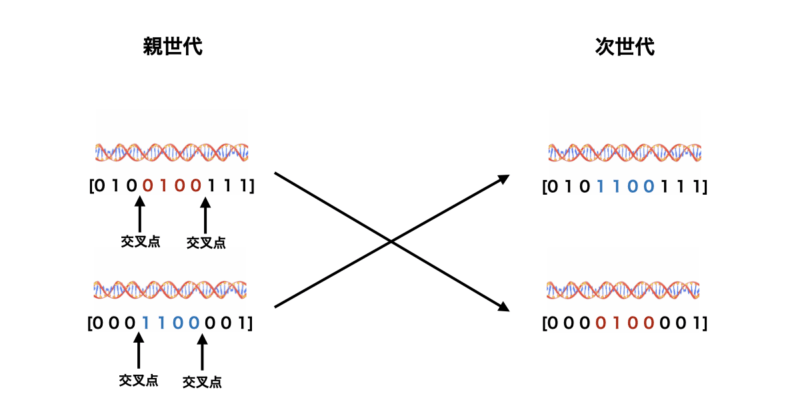

手順
- 親個体の遺伝子列を用意します(例: 親A =
11011、親B =00101)。 - ランダムに2つの交叉点を選びます(例: 2番目と4番目)。
- 交叉点で区切られた部分を親個体間で交換します(例: 子供A =
11101、子供B =00011)。
メリット&デメリット
- メリット: 2つの交叉点を使用するため、遺伝子的多様性が高まります。
- デメリット: 遺伝情報が大きく変更されるため、親の良い特徴が失われるリスクがあります。
一様交叉
次に一様交叉について説明していきます。
以下に原理、具体的な手順、メリット&デメリットについて記載します。
原理
- 一様交叉では、各遺伝子に対して独立に、どちらの親から引き継ぐかをランダムに決定します。通常、各遺伝子が50%の確率で親Aか親Bから継承されます。
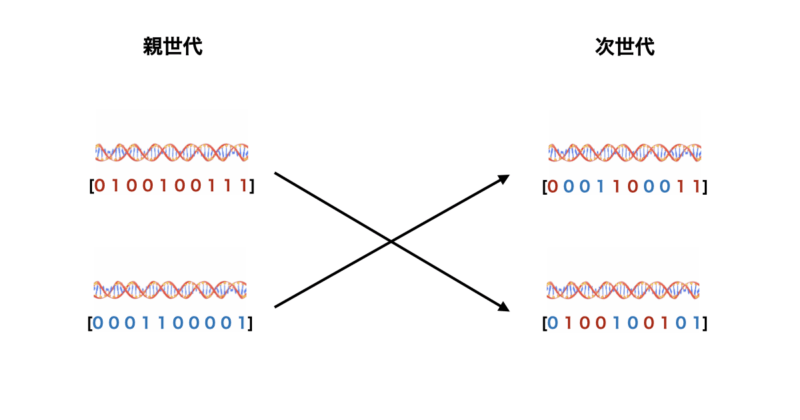

手順
- 親個体の遺伝子列を用意します(例: 親A =
11011、親B =00101)。 - 各遺伝子ごとにランダムに親Aか親Bから遺伝子を引き継ぎます。
- 新しい子供個体を生成します(例: 子供A =
10011、子供B =01101)。
メリット&デメリット
- メリット: 各遺伝子ごとに親を選ぶため、遺伝子的多様性が非常に高いです。
- デメリット: ランダム性が高いため、親の優れた遺伝子構造を失うリスクがあります。
突然変異(Mutation)
次の次世代生成の手法として突然変異について説明していきます。
突然変異(Mutation)は遺伝子の一部が特異的に変化するプロセスになっています。これにより、多様性を維持し、探索空間を広げるために重要な役割を果たします。
自然界と同じように遺伝子の一部のみが特異的に変化するような働きを模倣しています。
突然変異の特徴として、一部のみが変化した全く新しい解が探索されることで、局所最適解に陥るリスクが軽減されます。
突然変異の仕方にも種類があり、以下にそれぞれの種類と詳細について説明します。
ビット反転突然変異
まずはビット反転突然変異について説明していきます。
以下に原理、具体的な手順、メリット&デメリットについて記載します。
原理
ビット反転突然変異は、個体のバイナリ表現において、一つのビット(0または1)を反転させる突然変異方法です。
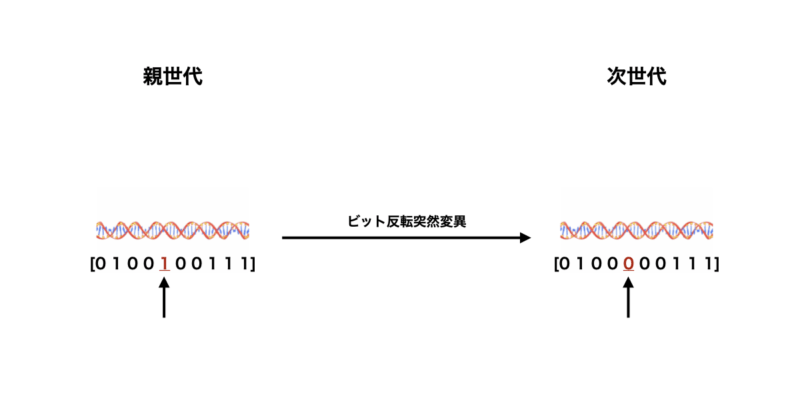

手順
- 突然変異を適用する個体のバイナリ表現を用意します(例:
10101)。 - ランダムに1つまたは複数のビット位置を選択します(例: 3番目のビット)。
- 選択されたビットを反転させます(例:
10001になる)。
メリット&デメリット
- メリット: 小さな変化を加えるため、個体の突然変異による破壊が少ない。
- デメリット: 大きな遺伝子の変化が期待できないため、最適解から遠い解に対しては効果が薄い。また、バイナリ表現に限定されるため、他の遺伝子表現に適用できない。
スワップ突然変異
次にスワップ突然変異について説明します。
以下に原理、具体的な手法、メリット&デメリットについて記載します。
原理
スワップ突然変異では、個体の遺伝子列内の2つの位置を選び、その位置にある遺伝子を交換します。
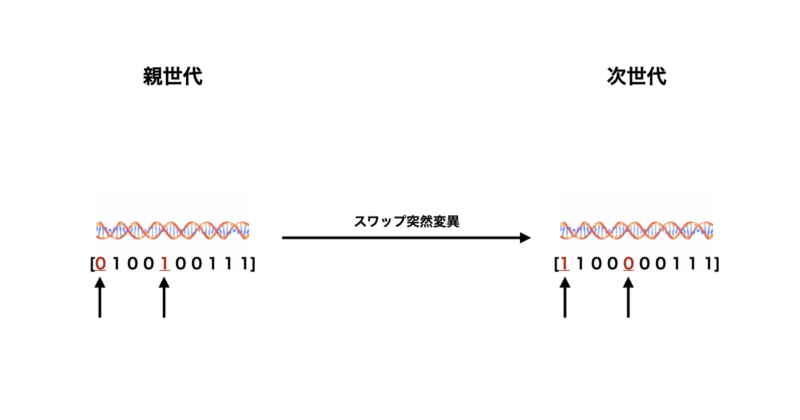

手順
- 突然変異を適用する個体の遺伝子列を用意します(例:
[1, 2, 3, 4, 5])。 - ランダムに2つの位置を選択します(例: 2番目と4番目)。
- 選択された位置にある遺伝子を交換します(例:
[1, 4, 3, 2, 5]になる)。
メリット&デメリット
- メリット: 順列を保ちながら突然変異を加えることができるため、巡回セールスマン問題などに適しています。
- デメリット: スワップする遺伝子の位置が離れていると、元の解から大きく離れる可能性があります。
ガウス突然変異
次にガウス突然変異について説明します。
以下に原理や具体的な手順、メリット&デメリットについて記載します。
原理
ガウス突然変異は、実数値を扱う遺伝子表現に適した手法で、ガウス分布に従って小さなランダムな変異を加えます。
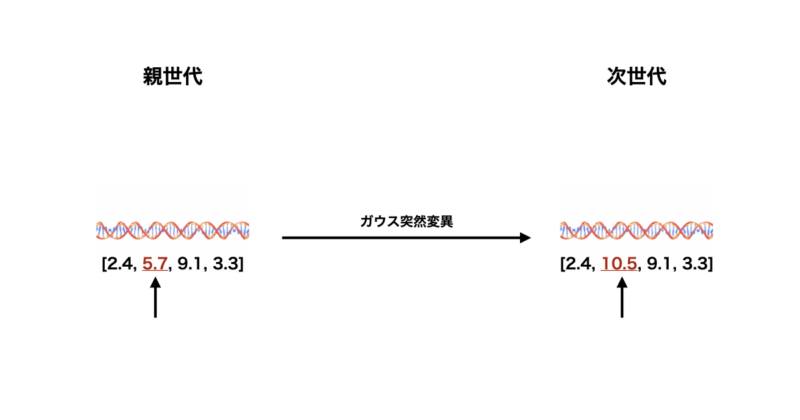

手順
- 突然変異を適用する個体の実数値遺伝子列を用意します(例:
[1.5, 2.3, 3.8])。 - 各遺伝子に対して、ガウス分布に基づいたランダムな値を加えます(例:
[1.5, 2.1, 4.0]になる)。
メリット&デメリット
- メリット: 実数値を直接扱うため、連続的な探索が可能です。
- デメリット: 突然変異の効果がガウス分布の平均値と標準偏差に大きく依存します。
Pythonでの実装
それでは実際にPythonで簡単な問題で遺伝的アルゴリズムを実装してみます。
今回は例としてOneMax問題を解くことにしましょう。
OneMax問題はバイナリビット(0 or 1)で表された数列が最大値、つまり全て1になるように解を最適化できるか?という問題になります。
具体的な最適化フローは以下の通りになっています。
- 第一世代の生成
生成方法はランダム生成として、集団サイズ100にて生成します。なお、各個体の遺伝子長は50となっています。
- 適応度の評価
それぞれの個体についてバイナリビットの合計値を適応度(max.50)として評価します。
- 次世代の生成(選択)
次世代の生成としてエリート選択により適応度が上位2つの個体をそのまま選択します。
- 次世代の生成(交叉)
次世代の生成として、親世代からランダムに2つ個体を選び、一点交叉により生成します。この時、一点交叉が起きる確率は80%で、一点交叉が起こらない場合はランダムに選択した親世代がそのまま次世代に引き継がれます。
- 次世代の生成(突然変異)
4にて生成した次世代について各ビットが2%の確率でビット反転突然変異が起きます。さらに、4-5の操作を次世代の集団サイズが100個に到達するまで繰り返します。
- 次世代の適応度評価
次世代の適応度を計算し、最適解(適応度=50)を引き当てるか世代数が100を超えたら終了。そうでなければ再度1-5の操作を繰り返す。
そして、上記のフローに従うように作成したコードが以下の通りとなります。
import random
# パラメータ設定
POPULATION_SIZE = 100 # 集団のサイズ
GENOME_LENGTH = 50 # 各個体の遺伝子長
CROSSOVER_RATE = 0.8 # 交叉の確率
MUTATION_RATE = 0.02 # 突然変異の確率
MAX_GENERATIONS = 100 # 最大世代数
# 適応度関数: 1の数をカウント
def fitness(individual):
return sum(individual)
# 初期集団をランダムに生成
def generate_population(size, length):
return [[random.randint(0, 1) for _ in range(length)] for _ in range(size)]
# ルーレット選択
def select(population):
max_fitness = sum(fitness(ind) for ind in population)
pick = random.uniform(0, max_fitness)
current = 0
for individual in population:
current += fitness(individual)
if current > pick:
return individual
# 1点交叉
def crossover(parent1, parent2):
if random.random() < CROSSOVER_RATE:
point = random.randint(1, GENOME_LENGTH - 1)
return parent1[:point] + parent2[point:], parent2[:point] + parent1[point:]
return parent1, parent2
# 突然変異
def mutate(individual):
for i in range(GENOME_LENGTH):
if random.random() < MUTATION_RATE:
individual[i] = 1 - individual[i] # 0なら1に、1なら0に反転
return individual
# メインループ
def genetic_algorithm():
population = generate_population(POPULATION_SIZE, GENOME_LENGTH)
for generation in range(MAX_GENERATIONS):
# 各個体の適応度を評価
population = sorted(population, key=fitness, reverse=True)
# 最適解が見つかったら終了
if fitness(population[0]) == GENOME_LENGTH:
print(f"解が見つかりました!世代数: {generation}")
print(f"最良個体: {population[0]}")
break
# 次世代を作成
next_generation = population[:2] # エリート選択で最良2個体はそのまま次世代へ
# 交叉と突然変異
while len(next_generation) < POPULATION_SIZE:
parent1 = select(population)
parent2 = select(population)
offspring1, offspring2 = crossover(parent1, parent2)
next_generation.append(mutate(offspring1))
next_generation.append(mutate(offspring2))
population = next_generation
else:
print("最大世代数に達しました。")
print(f"最良個体: {population[0]}")
print(f"適応度: {fitness(population[0])}")
if __name__ == "__main__":
genetic_algorithm()
'''
最大世代数に達しました。
最良個体: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1]
適応度: 47
'''上記コードを実行した結果は適応度47で最大世代数(100)に達して終了となりました。
各個体の遺伝子長が50だったので最適解に一歩及ばず終了となっていますね。
今回、ハイパーパラメータである交叉確率や突然変異確率は一点張りにしているので、もう少し数値を振って検討すると効率の良いアルゴリズムになるかもしれませんね。
ちなみに各世代ごとのヒストグラムをgif画像にして経時変化で確認できるようにしてみました。最初は適応度25程度を中心とした分布になっていますが、世代を追うごとに徐々にヒストグラム中心の適応度が高くなっており、適切に進化しているのがわかります。
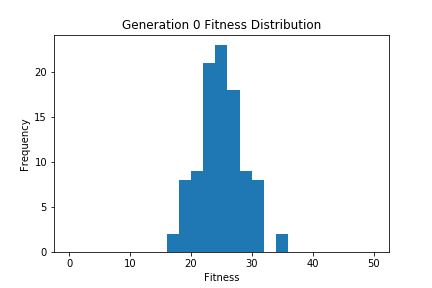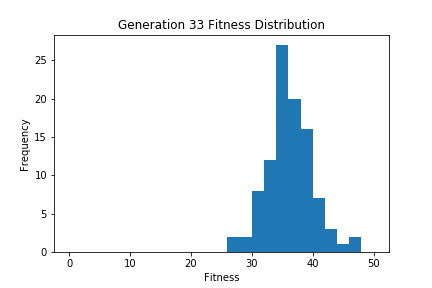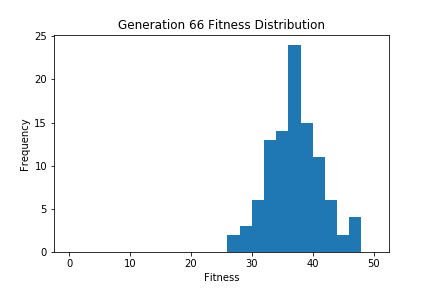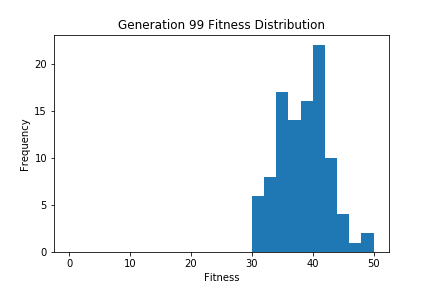

上記コードは特殊なライブラリなどは使用してませんので、実際に動かしたい人がいらっしゃればお試しいただければと思います。
学習ステップをさらに進めたい方へ
遺伝的アルゴリズム(GA)の基本的な概念を理解したら、
次は選択・交叉・突然変異といった操作が、探索の進み方や解の多様性にどう影響するのかを、
仕組みとして整理しておきたいところです。
その理解を深め、次の学習ステップへ進むためのインプットとしておすすめなのが、
『図解即戦力 機械学習&ディープラーニングのしくみと技術がこれ一冊でしっかりわかる教科書』です。
本書は、コード実装を主目的とした実践書ではなく、
遺伝的アルゴリズムを含む機械学習・最適化手法の考え方や処理の流れを、図解中心で整理する教科書です。
難しい数式や細かな実装に踏み込まず、
「なぜその操作が探索を前に進めるのか」「どこで探索が停滞・発散しやすいのか」といったポイントを
概念レベルで理解できる構成になっています。
数式やコードを追わずに“仕組みとして”整理できるため、
この先に学ぶパラメータ設計や応用(最適化・探索問題)への理解がスムーズになります。
「遺伝的アルゴリズムを使ってはいるが、なぜその設定で探索が進むのか説明できない」
「次は実装や応用に進みたいので、その前に全体像を整理しておきたい」
そんな方にとって、実装フェーズへ進む前段階のインプットとして最適な一冊です。
本書で理解の土台を固めてから実装や応用に取り組むことで、
“なんとなく回す”から“意図して設計・調整する”へと学習を一段前に進められます。
一方で「Pythonはこれから…」「数式で挫折したことがある…」という方もいらっしゃるかと思います。
そんな初学者の方でもpythonで機械学習を実装できるようになるためのロードマップとオススメの教材について以下の記事にまとめていますので、興味のある方はご覧になって下さい。
終わりに
以上が遺伝的アルゴリズムについての解説になります。生物の進化をアルゴリズムとして最適化するという思考がとても面白いですよね。同じ最適化手法としてベイズ最適化などが挙げられますが、これとはまた違った視点でのアルゴリズムになっているため、問題としているモデルに合わせて使い分けていきたいですね。