こんにちは!ぼりたそです!
今回は次元削減法の一つでデータ分析では基本とも言える主成分分析(PCA:Principal Component Analysis)について初学者の方でもわかりやすく説明していきたいと思います。
この記事は以下のポイントでまとめています。
- 主成分分析とは?
- 主成分分析のアルゴリズム
- Pythonで実行
- オススメ書籍
他の次元削減法としてt-SNE、UMAPについて解説した記事も過去に公開しているので、興味のある方は参照ください。
また、CSVファイルを入力するだけでPCAが実行できるコードも公開しているので、興味のある方はご参照ください。
それでは順に解説していきます。
主成分分析(PCA)とは?
まずは主成分分析について概要を説明していきます。
主成分分析(PCA)は、データの次元を削減し、データの可視化や解析をより簡潔にする手法です。多くの変数を持つデータを、より少ない数の「主成分」と呼ばれる新しい変数に変換して、データの本質的な情報を保ちながら、簡潔に表現することができます。
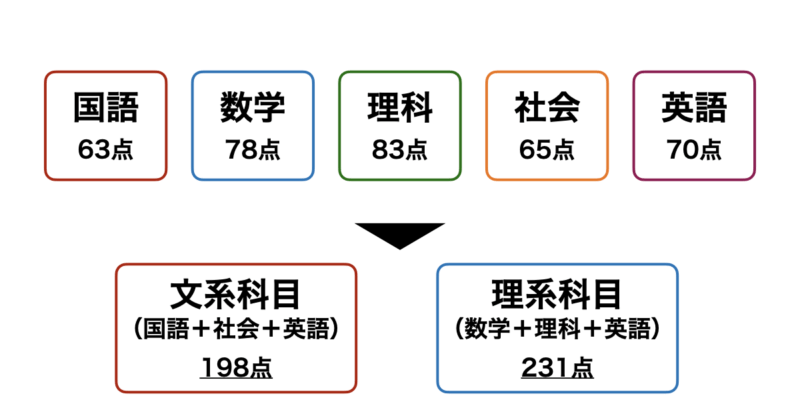
例えば、下図のように「国語」、「数学」、「理科」、「社会」、「英語」の5科目のテストのスコアデータがあるとします。
これを理系科目=「数学」+「理科」+「英語」、文系科目=「国語」+「社会」+「英語」とすることで5次元あったデータを二次元に圧縮することができます。この次元削減によりこの生徒はざっくり理系科目が得意な傾向にあることがわかります。

PCAはこのように元のデータからなるべく情報損失を抑えつつ、次元削減を行うことでデータの解釈や可視化を簡潔にしてくれるのです。
また、PCAについて上記で紹介した以外のメリット、さらにはデメリットも記載いたします。きちんとデメリットも理解した上で使用できるようになりたいですね。
■メリット
■デメリット
主成分分析のアルゴリズム
次に主成分分析(PCA)のアルゴリズムについて解説していきます。
PCAは基本的に以下の手順で行われます。
- データの標準化
- 共分散行列の計算
- 固有値と固有ベクトルの計算
- 主成分の選択
順に説明していきます。
データの標準化
まずはデータの標準化についてです。
PCAを実行する際は基本的にデータの標準化をしなければいけません。
標準化とは、変数ごとに平均を0、標準偏差を1に変換することを言います。
変数のスケールが異なる場合、例えば、身長[m]、年収[万円]のデータがあったとします。仮にそれぞれ数値が1増えた場合、身長が1m増えるとの年収が1万円増えるのでは訳が違いますよね。
こういったスケールの違いはPCAの結果に影響を与える可能性があるため、各変数を同じスケールに揃える必要があるのです。
共分散行列の計算
次に共分散行列の計算について説明します。
まず、例として標準化した2変数(X1,X2)データが以下のような二次元グラフで表せるとします。
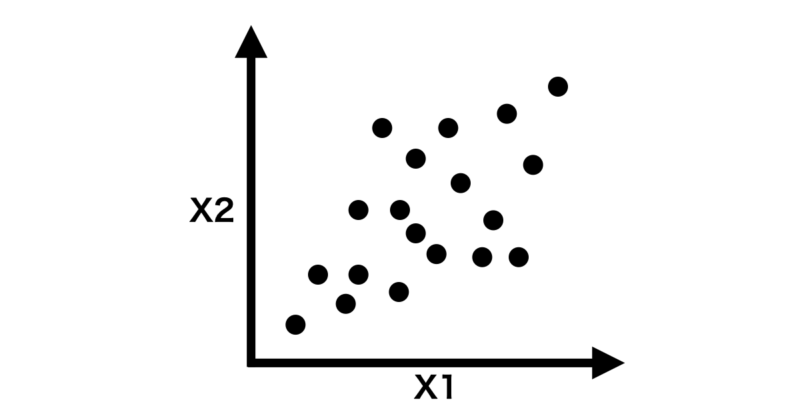

共分散行列を計算するということは、この変数同士がどれくらい相関しているか、どのくらいデータが分散しているかを計算することになります。
ちなみに共分散行列は以下のような行列式で表すことができます。
$$\mathbf{C} = \begin{pmatrix}
\text{Cov}(X_1, X_1) & \text{Cov}(X_1, X_2) \\
\text{Cov}(X_2, X_1) & \text{Cov}(X_2, X_2)
\end{pmatrix}$$
ここで $text{Cov}(X_i, X_j)$ は $X_i$ , $X_j$ の共分散であり、以下の式で求めることができます。
$$\text{Cov}(X_i, X_j) = \frac{1}{N} \sum_{k=1}^{N} (X_i^{(k)} – \mu_i)(X_j^{(k)} – \mu_j)$$
- $N$ はデータ点数
- $ X_i^{(k)}$ は $i$ 番目の変数の $k$ 番目のデータポイント
- $u_i$ は $i$ 番目の変数の平均値を表します。
この数式を使うことで、各変数間の共分散を求め、共分散行列を作成します。
固有値と固有ベクトルの計算
共分散行列を計算した後、次に行うのが 固有値と固有ベクトル の計算です。このステップで、データの分散を最もよく説明する「方向」(主成分)を見つけます。
固有ベクトルは、データの分散が最大となる方向(軸)を示します。データのパターンを捉えるために、新しい基準軸(主成分)を作り出すものです。
固有値は、各固有ベクトルがどれだけのデータの分散を説明しているかを示す大きさです。大きな固有値ほど、その固有ベクトル(主成分)がデータの分散をよく説明していることを意味します。
この固有ベクトルと固有値から主成分が決まり、先ほどの図で表すと次のようになるかと思います。
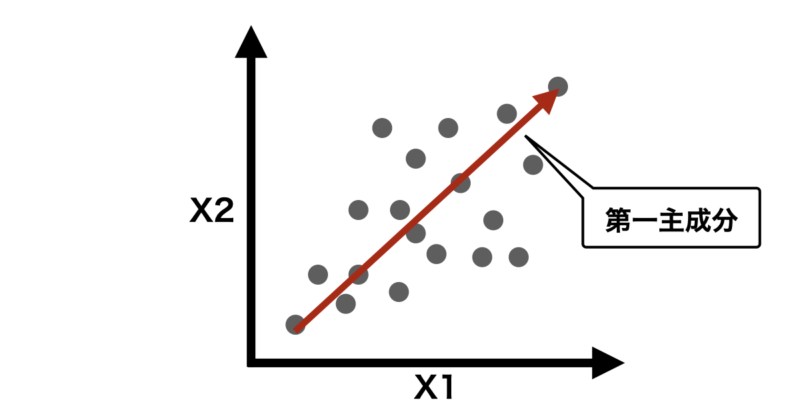

固有値と固有ベクトルは、次の式に従って定義されます
$$\mathbf{C} \mathbf{v} = \lambda \mathbf{v}$$
ここで、$C$ は共分散行列、$v$ は固有ベクトル、$\lambda$ は固有値です。
この式は、共分散行列 $C$ が固有ベクトル $v$ をかけると、その結果は固有ベクトルの長さが $\lambda$ 倍されたものと同じであることを意味しています。この式を解くことで、データの最も重要な方向(固有ベクトル)と、その方向の重要度(固有値)が求まります。
主成分の選択
PCAにおいて主成分を選択することは重要であり、次元削減やデータの要約を行うための鍵となります。ここでは、主成分の選択方法やその意義について詳しく説明します。
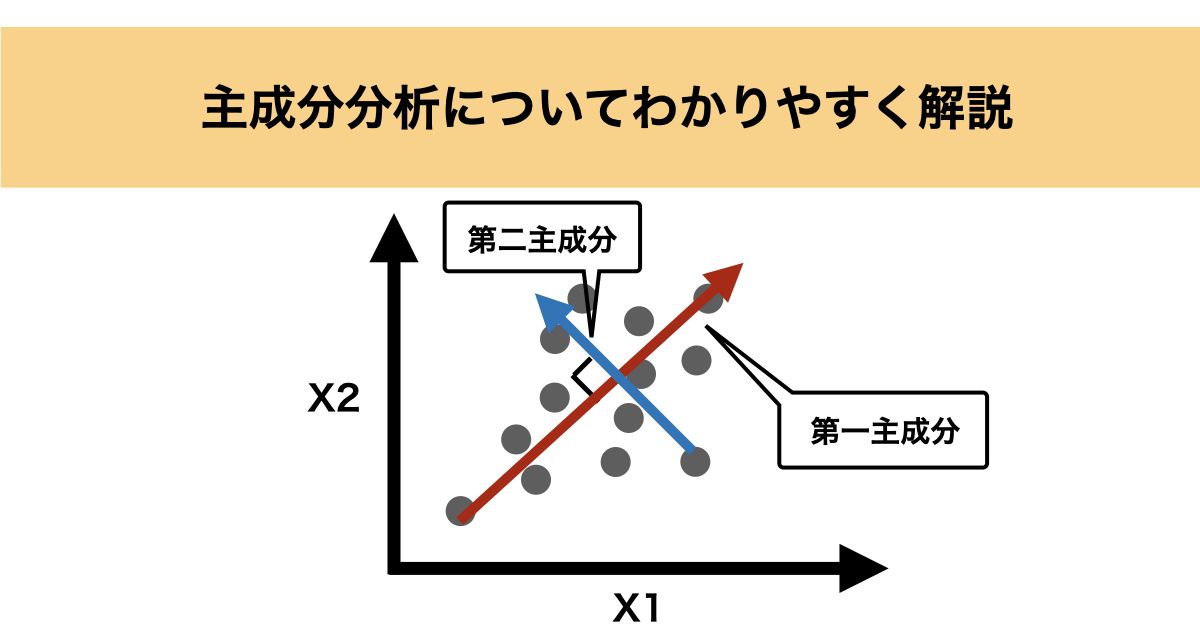
PCAでは第二主成分以降も先ほど説明した手順で順番に計算します。下の説明のように第一主成分以降はそれ以前の主成分に直行するように生成されます。
主成分同士が直行することは互いに独立であることを示し、異なる情報を持った軸になることを意味します。逆にほとんど同じ方向の主成分は同じような情報しか表現することができず、あまり意味がないことになります。
- 第1主成分 (PC1):データの分散が最大になる方向を表し、最も多くの分散を説明します。
- 第2主成分 (PC2):第1主成分に直交する(90度の角度で独立している)方向で、残りの分散を最大限に説明します。
- 以降の主成分:それぞれ前の主成分に直交する方向で、データの分散を説明する順番に計算されます。
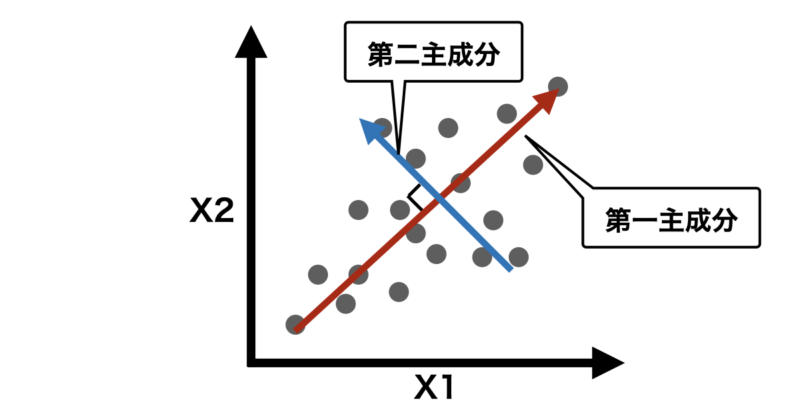

さて本題に戻りますが、新たに生成した第一〜第n主成分の中でもどの主成分を使用するかがが重要になってきます。
少ない数の主成分を使用することで次元削減による効果が大きくなりますが、情報の損失も大きくなってしまい、結果として精度が低いモデルになってしまうリスクがあります。その逆も同様です。
そこで、主成分の選択方法としてよく使用されるのが累積寄与率を基準にした手法です。
この方法では、各主成分がデータの分散をどれだけ説明しているかを示す「寄与率」と、それを累積した「累積寄与率」を計算し、それを基準にして使用する主成分の数を決定します。
寄与率は各主成分がデータ全体の分散をどの程度説明しているかを表します。第1主成分から順に、データの分散を多く説明する方向に沿って計算されます。
ここで、$\lambda_j$は第$j$主成分の固有値で、$\sum_{j=1}^{n} \lambda_j$は全ての固有値の合計です。
$$\text{寄与率} = \frac{\lambda_i}{\sum_{j=1}^{n} \lambda_j}$$
累積寄与率は主成分をいくつか選択したとき、それらの主成分がデータ全体の分散をどれだけ説明しているかを表します。累積的に寄与率を加算していくことで得られます。この累積寄与率が高いほど、選択した主成分が元のデータの情報をよく説明していることになります。
$$\text{累積寄与率} = \sum_{k=1}^{i} \text{寄与率}_k$$
この累積寄与率の閾値を通常80%から90%に設定することが多いです。
例えば、PCAにより以下のような主成分に対してその寄与率と累積寄与率が得られたとします。
| 主成分 | 寄与率 | 累積寄与率 |
|---|---|---|
| 第一主成分 | 50 | 50 |
| 第二主成分 | 30 | 80 |
| 第三主成分 | 10 | 90 |
| 第四主成分 | 5 | 95 |
| 第五主成分 | 3 | 98 |
| 第六主成分 | 2 | 100 |
累積寄与率が90%に達するまでの主成分を選択すると、第3主成分までを使用することになります。
累積寄与率は、データの情報量を損なわないように次元を削減するための指標として非常に有用です。主成分分析を効果的に行うために、累積寄与率の基準をしっかりと設定することが大切です。
主成分を選択したら後はその主成分を基にデータを反映すれば主成分分析は完了です。
番外編:主成分の解釈
PCAについて、次元削減によって少ない次元でデータを表現することができたとして、その主成分にどのような意味があるかを解釈する必要があります。
よく使用されるのは主成分負荷量であり、元の変数が各主成分にどの程度寄与しているかを示す指標です。
主成分に対して負荷量の絶対値が大きい変数ほど、その主成分に対して強く影響を与えると解釈できます。また、負荷量が正の場合、その変数は主成分の増加方向に寄与します。一方、負荷量が負の場合、その変数は主成分の減少方向に寄与します。
例えば、下のような主成分に対して元の変数の負荷量が得られたとします。
| 変数名 | 第一主成分 | 第二主成分 |
|---|---|---|
| 身長 | 0.6 | 0.1 |
| 体重 | 0.5 | 0.2 |
| 年齢 | 0.1 | 0.8 |
| 血圧 | 0.2 | 0.7 |
第一主成分 は、身長と体重に大きな荷重がついており、「身体の大きさ」を表している可能性が高いです。一方で第二主成分 は、年齢と血圧に大きな荷重がついているため、「健康状態や加齢に関連する要因」を表していると解釈できます。
このように負荷量を確認することで、主成分がデータのどの側面を表しているのかを理解し、データの構造を効果的に把握できます。
Pythonで実行
それでは最後にPythonを使用してPCAを実行してみましょう。
今回はボストンの住宅価格のデータを使用してPCAを実行してみました。
主成分の数は「累積寄与率が80%を超える最小の数」という条件にして選択しています。
実際のPythonコードは以下の通りです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import fetch_openml
# ボストンデータのロード
boston = fetch_openml(name='boston', version=1, as_frame=True)
df = boston.data
# 特徴量の確認
print("データの特徴量:\n", df.head())
# データの標準化
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df)
# PCAを適用して累積寄与率を計算
pca_temp = PCA()
pca_temp.fit(df_scaled)
# 寄与率と累積寄与率の計算
explained_variance_ratio = pca_temp.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)
# 累積寄与率が80%を超える最小の主成分数を選択
n_components = np.argmax(cumulative_variance_ratio >= 0.8) + 1
print(f"\n累積寄与率80%に達するための主成分数: {n_components}")
# 選択した主成分数でPCAを再実行
pca = PCA(n_components=n_components)
pca_result = pca.fit_transform(df_scaled)
# 結果をデータフレームに変換
pca_df = pd.DataFrame(pca_result, columns=[f'Principal Component {i+1}' for i in range(n_components)])
# 主成分負荷量
components = pca.components_
loadings_df = pd.DataFrame(components.T, columns=[f'Principal Component {i+1}' for i in range(n_components)], index=df.columns)
print("\n主成分負荷量:\n", loadings_df)
# 寄与率と累積寄与率のグラフを作成
plt.figure(figsize=(10, 6))
plt.bar(range(1, len(explained_variance_ratio) + 1), explained_variance_ratio, alpha=0.5, align='center', label='Individual explained variance')
plt.step(range(1, len(cumulative_variance_ratio) + 1), cumulative_variance_ratio, where='mid', label='Cumulative explained variance', color='red')
plt.xlabel('Principal Component Index')
plt.ylabel('Explained Variance Ratio')
plt.title('Explained Variance Ratio and Cumulative Variance')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
#plt.savefig('pca.png')使用した変数13個に対して生成した主成分13個の寄与率と累積寄与率が以下の通りになります。第一主成分が50%近い寄与率を示しており、それ以降の主成分はそこまで寄与していないようですね。
今回、累積寄与率80%を超える最小の数としているので使用される主成分は5個となります。元が13個の変数でしたので、かなり次元削減できたのではないでしょうか。
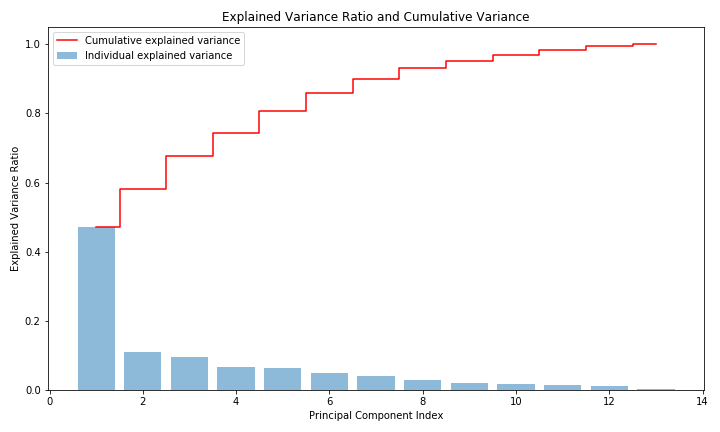

また、負荷量の計算もできるようにしてあるので、興味のある方は各主成分がどのような特徴を持っているか確認してみてもいいかもしれません。
学習ステップをさらに進めたい方へ
PCAの基本的な概念を理解したら、
次はなぜその方向が「主成分」と呼ばれるのか、分散最大化や次元削減がデータの見え方をどう変えるのかを、
仕組みとして整理しておきたいところです。
その理解を深め、次の学習ステップへ進むためのインプットとしておすすめなのが、
『図解即戦力 機械学習&ディープラーニングのしくみと技術がこれ一冊でしっかりわかる教科書』です。
本書は、コード実装を主目的とした解説書ではなく、
PCAを含む機械学習手法の構造・考え方・処理の流れを、図解中心で丁寧に解説する教科書です。
難しい数式に踏み込まず、回帰・分類・クラスタリングまでを通して、
「なぜその変換が行われるのか」「どんな情報が残り、何が捨てられるのか」をブラックボックス化せずに理解できます。
たとえばPCAについても、
- 分散を最大化するとはどういう意味か
- 主成分同士が直交する理由
- 次元削減がノイズ除去や可視化にどうつながるのか
といった点を、数式やコードを追わずに概念として整理できるため、
この先の前処理設計や、t-SNE・UMAPといった他の次元削減手法との比較にもスムーズに進めます。
「PCAを使ってはいるが、なぜその軸になるのか説明できない」
「次は実装や応用に進みたいので、その前に仕組みを整理しておきたい」
そんな方にとって、実装フェーズへ進む前段階のインプットとして最適な一冊です。
本書で理解の土台を固めたうえで実装に取り組むことで、
“とりあえず次元削減する”から“意図を持って使い分ける”へと学習を一段前に進められます。
一方で「Pythonはこれから…」「数式で挫折したことがある…」という方もいらっしゃるかと思います。
そんな初学者の方でもpythonで機械学習を実装できるようになるためのロードマップとオススメの教材について以下の記事にまとめていますので、興味のある方はご覧になって下さい。
終わりに
以上が主成分分析の解説となります。次元削減の中でも基本となる手法ですのでぜひ使いこなしていきたいですね。また次元削減の手法はUMAPなど他にもありますので、また別の機会にご紹介できればと思います。