こんにちは!ぼりたそです!
今回は説明変数が格納されたCSVを入力するだけで主成分分析(PCA)を実行するPythonコードをご紹介したいと思います。
また、この記事は以下のポイントでまとめています。
- 主成分分析(PCA)とは?
- 実装コードの仕組み
- 実装コードと解説
それでは順番に説明していきます。
主成分分析(PCA)とは?
まずは主成分分析について概要を説明していきます。
主成分分析(PCA)は、データの次元を削減し、データの可視化や解析をより簡潔にする手法です。多くの変数を持つデータを、より少ない数の「主成分」と呼ばれる新しい変数に変換して、データの本質的な情報を保ちながら、簡潔に表現することができます。
例えば、下図のように「国語」、「数学」、「理科」、「社会」、「英語」の5科目のテストのスコアデータがあるとします。
これを理系科目=「数学」+「理科」+「英語」、文系科目=「国語」+「社会」+「英語」とすることで5次元あったデータを二次元に圧縮することができます。この次元削減によりこの生徒はざっくり理系科目が得意な傾向にあることがわかります。
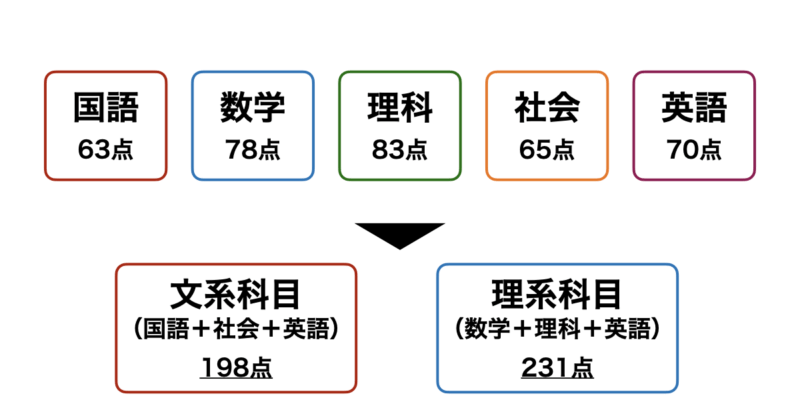
PCAはこのように元のデータからなるべく情報損失を抑えつつ、次元削減を行うことでデータの解釈や可視化を簡潔にしてくれるのです。
PCAの詳細について以前記事にまとめましたので、興味のある方は参照いただければと思います。
実装コードの仕組み
次に実装コードの仕組みについて解説していきます。
今回実装したコードは入力ファイル1つを設定することで3つのファイルが出力されます。それぞれのファイルの説明は以下の通りです。
◆入力ファイル
- インプット用CSVファイル(input_csv):
主成分分析を実行したいデータをCSVとしたファイル。目的変数は最初の列に格納するようにしてください(目的変数無しでも可)。また、データは数値のみとしてください。
◆出力ファイル
- 主成分変換後のCSVデータ(transformed_data.csv):
インプット用CSVファイルを主成分変換したデータファイル。最初の列に目的変数が格納されており、以降の列には主成分変換された説明変数が格納されている。
- 寄与率&累積寄与率のデータ(explained_variance.csv):
PCAを実行した際の各主成分に対する寄与率及び累積寄与率を格納したCSVファイル。
- 主成分負荷量のデータ(loadings.csv):
PCAを実行した際の各種成分に対する負荷量を格納したCSVファイル。
変換用データをインプットしたら自動で結果が出力されるものとお考えください。
実装コードと解説
それでは実装コードとその解説をしていきたいと思います。
実装したPythonコードは以下の通りです。
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
def perform_pca(input_csv, output_transformed_csv, output_loadings_csv, output_explained_variance_csv, target_col_num, explained_variance_threshold=0.95):
# CSVデータの読み込み
data = pd.read_csv(input_csv)
# 目的変数と説明変数に分ける
target_data = data.iloc[:, :target_col_num] # 最初のtarget_col_num列を目的変数として抽出
explanatory_data = data.iloc[:, target_col_num:] # 残りを説明変数として抽出
# 標準化
scaler = StandardScaler()
explanatory_data_scaled = scaler.fit_transform(explanatory_data)
# PCAの実行
pca = PCA()
pca.fit(explanatory_data_scaled)
# 寄与率と累積寄与率の計算
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)
# データフレームにまとめる
variance_df = pd.DataFrame({
'Explained Variance Ratio': explained_variance_ratio,
'Cumulative Variance Ratio': cumulative_variance_ratio
}, index=[f'PC{i+1}' for i in range(len(explained_variance_ratio))])
# CSVで出力
variance_df.to_csv('explained_variance.csv', index=True)
# 累積寄与率に基づいて主成分数を選定
cumulative_explained_variance = pca.explained_variance_ratio_.cumsum()
num_components = (cumulative_explained_variance < explained_variance_threshold).sum() + 1
# 選定した主成分数で再度PCAを実行
pca = PCA(n_components=num_components)
transformed_data = pca.fit_transform(explanatory_data_scaled)
# 主成分の負荷量を取得
loadings = pd.DataFrame(pca.components_.T,
columns=[f'PC{i+1}' for i in range(num_components)],
index=data.columns[target_col_num:])
# 負荷量をCSVとして保存
loadings.to_csv(output_loadings_csv, index=True)
# 変換したデータをDataFrameにして保存
transformed_df = pd.DataFrame(transformed_data, columns=[f'PC{i+1}' for i in range(num_components)])
transformed_df = pd.concat([target_data.reset_index(drop=True), transformed_df], axis=1)
transformed_df.to_csv(output_transformed_csv, index=False)
print(f'PCA実行完了。累積寄与率{explained_variance_threshold}に基づく主成分数: {num_components}')
# 使用例
perform_pca(
input_csv='boston_data.csv', # 入力するCSVファイルのパス
output_transformed_csv='transformed_data.csv', # 変換後のデータを保存するCSVファイルのパス
output_loadings_csv='loadings.csv', # 主成分の負荷量を保存するCSVファイルのパス
output_explained_variance_csv='explained_variance.csv', # 寄与率と累積寄与率を保存するCSVファイルのパス
target_col_num=1, # 目的変数の列数
explained_variance_threshold=0.8 # 累積寄与率の閾値
)
PCAを実行してファイルを出力する関数を設定しており、関数は大きく5つのブロックに分かれています。
- 引数の設定
- データの前処理
- 寄与率&累積寄与率の計算
- 主成分数の選定
- 主成分負荷量の取得
- 主成分変換後のデータ取得
以下、順に解説していきます。
引数の設定
まずは関数の引数について説明していきます。
引数は下に示すように6つ設定する必要があります。
def perform_pca(input_csv, output_transformed_csv, output_loadings_csv, output_explained_variance_csv, target_col_num, explained_variance_threshold=0.95):引数の概要については以下の通りです。
| 引数 | 説明 |
|---|---|
| input_csv | 主成分分析を実行したいCSVファイルのパス |
| output_transformed_csv | 主成分変換されたデータを保存するCSVファイルのパス |
| output_loadings_csv | 主成分負荷量が格納されたデータを保存するCSVファイルのパス |
| output_explained_variance_csv | 各主成分の寄与率や累積寄与率が格納されたデータを保存するCSVファイルのパス |
| target_col_num | 目的変数の数。0でも実行可能。 |
| explained_variance_threshold | 累積寄与率の閾値を設定します(0~1.0)。この閾値に基づいて、必要な主成分数が決定されます。デフォルトは0.95で設定されており、元のデータの95%を説明できる主成分数が選ばれます。 |
データの前処理
次にデータの前処理についてです。
実装コードの中では以下の部分で処理しています。
# CSVデータの読み込み
data = pd.read_csv(input_csv)
# 目的変数と説明変数に分ける
target_data = data.iloc[:, :target_col_num] # 最初のtarget_col_num列を目的変数として抽出
explanatory_data = data.iloc[:, target_col_num:] # 残りを説明変数として抽出
# 標準化
scaler = StandardScaler()
explanatory_data_scaled = scaler.fit_transform(explanatory_data)まずは、主成分分析を実行したいデータが格納されているCSVを読み込み、データフレームに変換します。これは関数の引数として設定しているinput_csvから読み込みます。
次に読み込んだデータを目的変数と説明変数に分けています。目的変数の数はtarget_col_numで設定した数値になっており、残りを説明変数として抽出しています。
最後に抽出した説明変数を標準化することでPCAを実行する前処理は完了です。
寄与率&累積寄与率の計算
次に寄与率&累積寄与率の計算について説明します。
実装コードでは以下の部分で処理しています。
# PCAの実行
pca = PCA()
pca.fit(explanatory_data_scaled)
# 寄与率と累積寄与率の計算
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)
# データフレームにまとめる
variance_df = pd.DataFrame({
'Explained Variance Ratio': explained_variance_ratio,
'Cumulative Variance Ratio': cumulative_variance_ratio
}, index=[f'PC{i+1}' for i in range(len(explained_variance_ratio))])
# CSVで出力
variance_df.to_csv('explained_variance.csv', index=True)まずは先ほど標準化した説明変数のデータで主成分分析を実行してしまいます。
その上ですべての主成分に対して寄与率をexplained_variance_ratio、累積寄与率をcumulative_variance_ratioに格納します。
さらに計算した寄与率、累積寄与率をデータフレームにまとめ、最後にCSVファイルとして出力しています。
出力されたファイルは以下のように、主成分に対して1列目が寄与率、2列目が累積寄与率が格納されています。
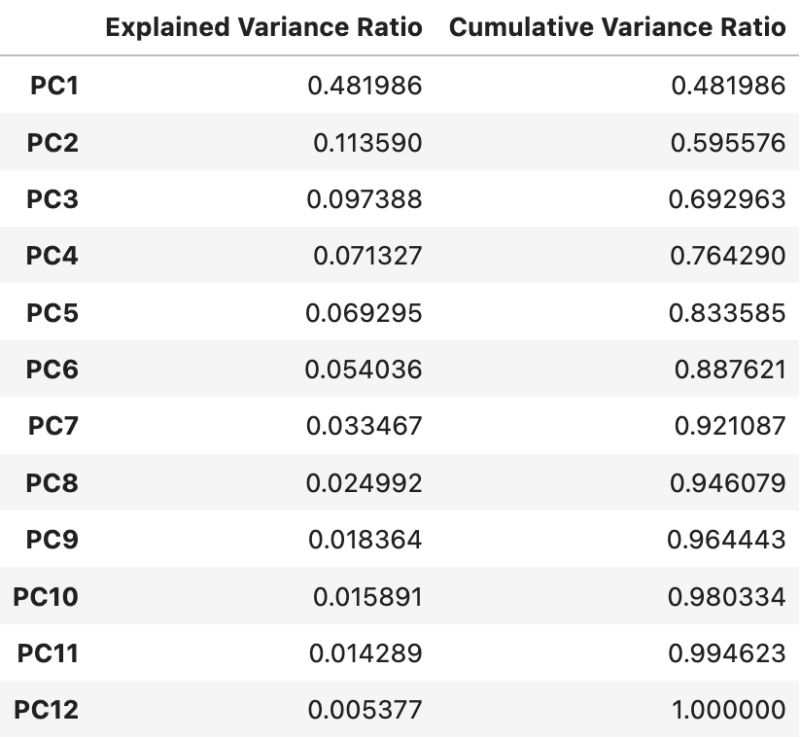

主成分数の選定
次に主成分の選定について説明していきます。
実装コードの中では以下の部分で処理しています。
# 累積寄与率に基づいて主成分数を選定
cumulative_explained_variance = pca.explained_variance_ratio_.cumsum()
num_components = (cumulative_explained_variance < explained_variance_threshold).sum() + 1このコードではまず、累積寄与率を計算しており、pca.explained_variance_ratio_ は、寄与率のnumpy配列を示します。また、.cumsum() は累積和を計算するメソッドであり、これにより累積寄与率をcumulative_explained_varianceにnumpy配列として格納しています。
cumulative_explained_variance < explained_variance_threshold では、累積寄与率が指定した閾値(explained_variance_threshold)未満であるかどうかを判定します。そのため、累積寄与率が閾値を超えていない主成分の数を示す真偽値の配列を返します。
さらに、.sum() は、真(True)の数を数えるため、閾値を超えていない主成分の数を数えます。+ 1 は、累積寄与率が閾値に達した時点の主成分を含めるために追加しています。そのため、累積寄与率が指定した閾値(例えば95%)に達するまでに必要な最小の主成分数を計算し、その結果を num_components に格納しています。
主成分負荷量の取得
次に主成分負荷量の取得について説明します。
実装コードでは以下の部分で処理しています。
# 選定した主成分数で再度PCAを実行
pca = PCA(n_components=num_components)
transformed_data = pca.fit_transform(explanatory_data_scaled)
# 主成分の負荷量を取得
loadings = pd.DataFrame(pca.components_.T,
columns=[f'PC{i+1}' for i in range(num_components)],
index=data.columns[target_col_num:])
# 負荷量をCSVとして保存
loadings.to_csv(output_loadings_csv, index=True)ここでは、まず先ほど選定した主成分数で再度PCAを実行します。これにより変換された主成分に対して主成分負荷量をloadingsとして取得しています。
pca.components_ は、PCAで学習された各主成分に対する成分行列(負荷量)を表します。これは、各説明変数が各主成分にどの程度寄与しているかを示す値です。
pca.components_ は形状が (num_components, num_features) の配列で、各行が各主成分(PC1, PC2, …)に対応し、各列が元の特徴量に対応します。
.T(転置) を行うことで、形状が (num_features, num_components) となり、各行が元の特徴量に対応し、各列が主成分に対応するようにします。
実際に取得したCSVは以下のようになっています。今回の累積寄与率の閾値を80%に設定しているので、主成分数は5つとなっています。
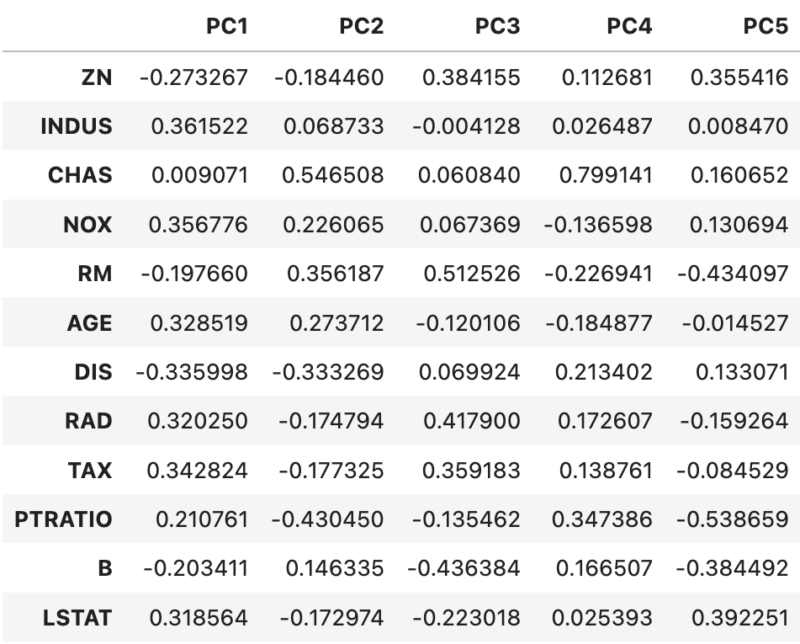

主成分変換後のデータ取得
最後に主成分変換後のデータ取得について説明いたします。
実装コードでは以下の部分で処理しています。
# 変換したデータをDataFrameにして保存
transformed_df = pd.DataFrame(transformed_data, columns=[f'PC{i+1}' for i in range(num_components)])
transformed_df = pd.concat([target_data.reset_index(drop=True), transformed_df], axis=1)
transformed_df.to_csv(output_transformed_csv, index=False)特に詳細な説明をすることもないのですが、先ほど実行したPCAに基づいて主成分変換したデータをデータフレームに格納して、CSVファイルとして出力しています。
実際に出力したファイルは以下のようになっています。一列目が標準化などの処理も実行していない目的変数となっており、以降の列が主成分変換されたデータとなっています。
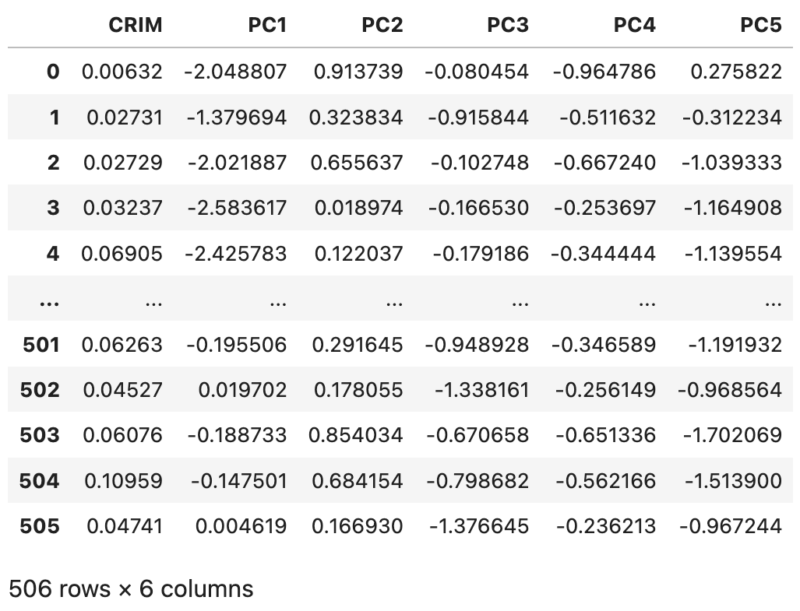

終わりに
以上が、CSVを入力するだけでPCAを実行するコードの説明になります。使い勝手が悪い箇所もあると思いますが、ご自由にアレンジしてご利用ください。次元削減は他にも様々な種類がありますので、またの機会にご紹介できればと思います。