こんにちは!ぼりたそです!
今回は機械学習モデルを解釈する手法としてSHAP(SHpley Additive exPlanations)について、その重要性やアルゴリズムについてわかりやすく解説していきたいと思います。
この記事は以下のポイントでまとめています。
- 機械学習モデルの予測の理由
- Shapley値について
- SHAPの実行
- SHAPで様々な可視化を実行
- 参考書籍
また、同じように機械学習モデルの解釈法についてPFIやPD, ICEについても過去の記事でまとめているので、興味のある方はご参照ください。
それでは、SHAPについて順に解説していきます。
機械学習モデルの予測の理由
まず、機械学習モデルの予測の理由を考える重要性について解説していきます。
機械学習モデルはほとんどの場合、ブラックボックスになります。その結果、なぜその予測値になったのか?どの特徴量が寄与したのか?などがわからない状況に陥ってしまうのです。
なので、AIに予測させても、なぜその予測になったのか理由が不明となり、会社で重要な判断を下す際に困ってしまいます。
そこで、機械学習がなぜその予測値を出したのかを解釈するSHAP(SHpley Additive exPlanations)という手法についてフォーカスしていきます。
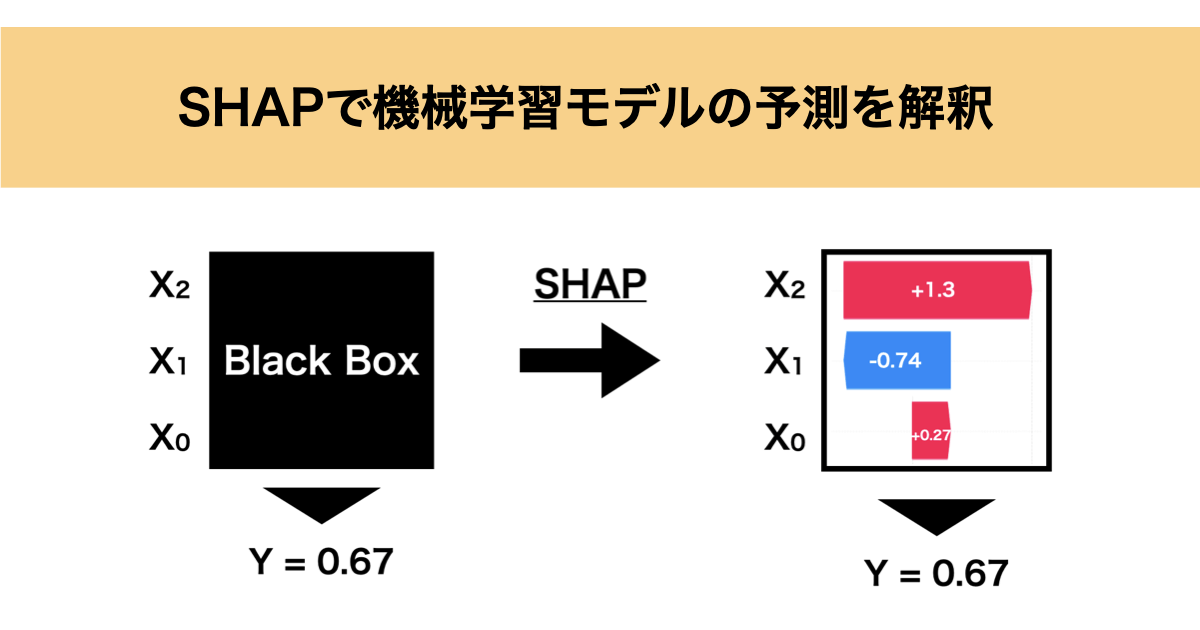
SHAPは下の図のように機械学習で出された予測に対して、特徴量の寄与などを算出することで各特徴量がどのように影響しその予測値に至ったのかを解釈することができます。
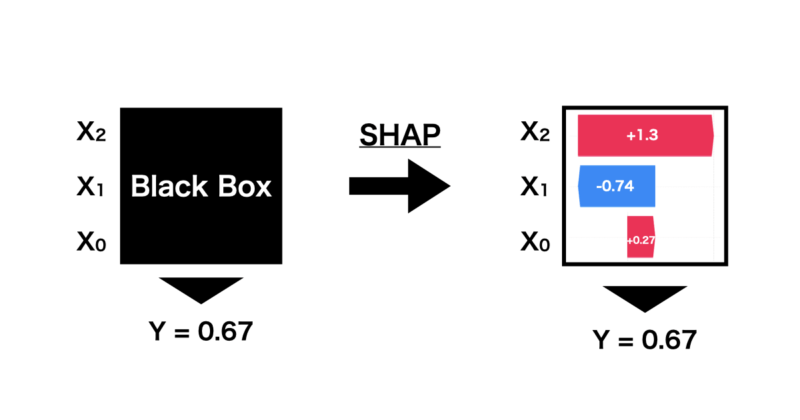

SHAPは協力ゲーム理論に基づいたShapley値を応用して予測値を解釈しています。次にこのShapley値について詳しく解説していきます。
Shapley値について
SHAPはShapley値を基にして予測値における特徴量の影響を算出していますが、このShapley値について協力ゲーム理論を例にとって説明していきます。
例えば、ある報酬付きのゲーム大会があると仮定して参加者にA、B 、Cがいるとします。
この大会は単独で参加してもいいですし、他の人とチームを組んで参加することもできるとします。
ここで、参加者により獲得できる報酬額が決まり、それが以下のテーブルに示す通りとなっています。
| 参加者 | 報酬[万円] |
|---|---|
| A | 6 |
| B | 4 |
| C | 2 |
| A, B | 20 |
| A, C | 15 |
| B, C | 10 |
| A , B, C | 24 |
この時、A ,B ,Cの三人で参加した場合、報酬の24万円をどのように配分するのが正解でしょうか?
恐らく、それぞれの貢献度に応じて報酬を分配するのが無難なように思えます。
では、その貢献度をどのようにして計ればいいのでしょうか?
ここで限界貢献度という概念を追加していきます。
限界貢献度とは各人が大会に参加することで得られる追加報酬から計算します。
例えば、Aの場合では
- 「参加者0」→ 「A参加」:6 – 0 = 6
- 「B参加」→ 「A,B参加」:20 – 4 = 16
- 「C参加」 → 「A,C参加」:15 – 2 = 13
- 「B,C参加」 → 「A ,B,C参加」:24 – 10 = 14
となり、A,B,Cが協力して参加した場合、Aの限界貢献度は14万円分ということになります。
しかし、ここで注意したいのがAが参加するタイミングで貢献度が変わってしまうということで、実際に参加順で以下のようにA, B,Cの限界貢献度が変化します。
| 参加順 | Aの限界貢献度 | Bの限界貢献度 | Cの限界貢献度 |
|---|---|---|---|
| A → B → C | 6 | 14 | 4 |
| A → C → B | 6 | 9 | 9 |
| B → A → C | 16 | 4 | 4 |
| B → C → A | 14 | 4 | 6 |
| C → A → B | 13 | 9 | 2 |
| C → B → A | 14 | 8 | 2 |
| 平均の限界貢献度 | 11.5 | 8 | 4.5 |
このように計算するとA,B,Cが協力して大会の報酬を獲得した場合、A:11.5万円、B:8万円、C:4.5万円と分けるのが限界貢献度に従った分け方と言えます。
また、上記で計算した平均的な限界貢献度をShapley値と呼びます。
SHAPではこのShapley値の考え方を応用し、特徴量がわかっている/わかっていない状態での予測値の差から特徴量の限界貢献度を計算しています。
SHAPの実行
それでは実際にSHAPを実行していきます。
今回は例として $X = (X_0, X_1, X_2)$ としたとき、以下の $f(X)$ に従うデータを生成します。
$$f(X) = X_0\ -\ 4^{X_1} + \exp ( X_2)$$
生成したデータに対してランダムフォレスト回帰を行い、予測した1点に対してSHAPを実行してみました。
import numpy as np
import pandas as pd
import shap
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
# 訓練用データの生成
np.random.seed(0)
X_train = pd.DataFrame({
'X0': np.random.uniform(-2, 2, 100),
'X1': np.random.uniform(-2, 2, 100),
'X2': np.random.uniform(-2, 2, 100)
})
# ターゲット変数の計算
y_train = X_train['X0'] - 4**(X_train['X1']) + np.exp(-X_train['X2'])
# モデルの訓練
model = RandomForestRegressor(n_estimators=100, random_state=0)
model.fit(X_train, y_train)
# 予測用データの生成(ランダムに1点)
X_test = pd.DataFrame({
'X0': np.random.uniform(-2, 2, 1),
'X1': np.random.uniform(-2, 2, 1),
'X2': np.random.uniform(-2, 2, 1)
})
# SHAPの値を計算
explainer = shap.TreeExplainer(model)
shap_values_test = explainer.shap_values(X_test)
# グラフの表示(Waterfall Plot)
for i in range(1): # 予測用データの1点を表示
shap.waterfall_plot(shap.Explanation(values=shap_values_test[i], base_values=explainer.expected_value, data=X_test.iloc[i]))
出力結果が以下の通りとなります。下のグラフはwaterfall plotと言って縦軸に特徴量とその値、横軸には予測した $f(X)$ に対する特徴量の貢献度が可視化されています。
今回は $X_0 = 1.626$ , $X_1 = 1.096$ , $X_2 = -0.667$ に対して予測値が $f(X) = -0.484$ となっており、この時の特徴量の貢献度が示されています。
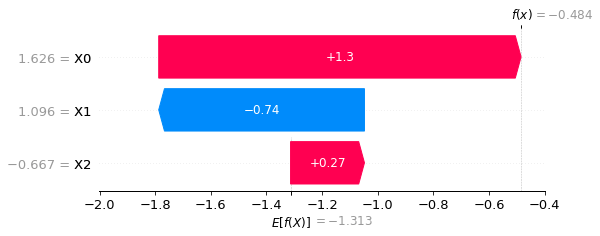

なお、$E[f(X)]$ は予測値の平均的な期待値であり、ベースラインくらいの認識で問題ありません。このベースラインから各特徴量の貢献度を足し合わせることで予測値が算出されるようになっています。
SHAPで様々な可視化を実行
これまでSHAPによる予測点に対する解釈とミクロな視点で説明してきました。
しかし、SHAPは予測点のミクロな解釈だけでなく、データ全体のマクロな解釈も可能です。
SHAPの考え方として、ある一点の予測値における各特徴量の貢献度を算出していましたが、これを全ての点に対して算出し、その貢献度を平均化することでデータ全体から見た特徴量の貢献度やその分布を可視化することができます。
以下、SHAPによるマクロな視点での様々な可視化方法についてご紹介していきます。
特徴量重要度
まずはデータ全体から特徴量重要度を可視化する手法について説明していきます。
先ほど少し説明しましたが、SHAPは一つの予測点における特徴量の貢献度を算出していますが、これを全てのデータで行い、平均化することでデータ全体における特徴量重要度として可視化することができます。
SHAPの実行にて紹介したコードに以下のコマンドを追加することでデータ全体から見た特徴量重要度をグラフ化することができます。
# 1. Bar Plotの可視化
shap.summary_plot(shap_values, X, plot_type="bar")実行結果は以下の通りです。縦軸が特徴量となっており、横軸がその重要度を示しています。
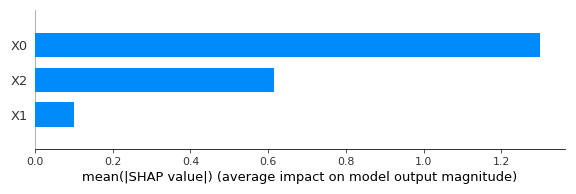

特徴量重要度を算出する手法としてPFIがありますが、SHAP一つでPFIの機能も実装できるということですね。
PFIについては以前まとめていますので、興味のある方は以下の記事を参考にしていただければと思います。
貢献度の分布
先ほどは特徴量重要度の可視化を行いましたが、これはあくまでデータ全体で平均化した重要度に過ぎません。
SHAPでは重要度についてbeeswarm plotとして各データの分布として可視化することができます。
SHAPの実行にて紹介したコードに以下のコマンドを追加することで可視化することができます。
# 2. Beeswarm Plot(Summary Plot)の可視化
shap.summary_plot(shap_values, X)実行結果は以下の通りです。
縦軸に特徴量、横軸に各データ(インスタンス)ごとのSHAP値をプロットしています。また、プロットの色は赤いほど特徴量の値が大きく、青いほど小さいということになります。
なので、SHAP値が大きく、プロットが赤い傾向があれば正相関、青ければ負相関であるとわかります。
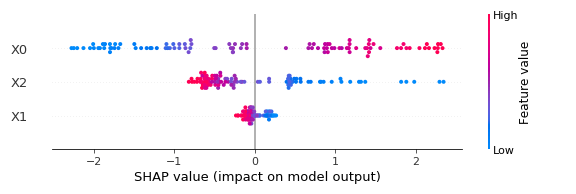

今回の例で言うと、 $X_0$ はSHAP値の幅が広く、SHAP値が大きいほど特徴量も大きいことから正相関の傾向にあるようです。
$X_2$ は正のSHAP値が幅広く、SHAP値が大きいほど特徴量が小さいことから負相関の傾向があるようです。
このように特徴量重要度だけではなく、特徴量の貢献度を各データごとに分布かすることで様々な情報を得ることができます。
特徴量に対する予測値の可視化
最後に特徴量の変化に対する予測値の可視化方法についてご紹介します。
特徴量の変化に対する予測値の可視化はPD(Partial Dependence)と呼ばれ、SHAPでも実行できるのです。
PDについては過去にまとめておりますので、ご興味のある方は以下の記事を参考にしていただければと思います。
SHAPの実行で紹介したコードに以下のコマンドを追加することで可視化できます。
# 特定の特徴量 'X0' を選択してプロット
shap.dependence_plot('X0', shap_values, X)実行した結果は以下の通りです。縦軸が特徴量のSHAP値となっており、横軸が特徴量の値となっています。また、選択した特徴量と交互作用の強い特徴量を自動で選択して、値の高低で色付けされています。
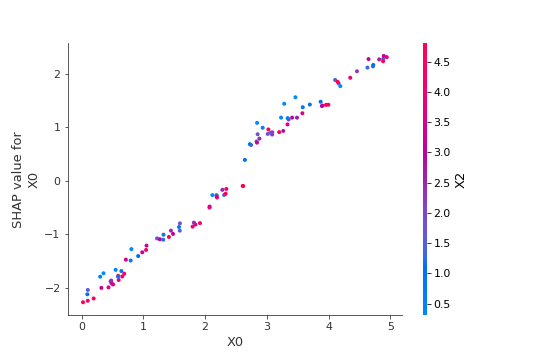

今回は特徴量として $X_0$ を選択していますが、 $X_0$ が大きくなるほどSHAP値も大きくなっていることがわかります。生成した関数から $X_0$ は正相関で線形的に作用するため正しく計算できていると言えます。
以上、簡単ではありますがSHAPにおいて様々な尺度による解釈について、いくつか可視化手法をご紹介させていただきました。
参考書籍
最後に本記事を作成するにあたり参考にさせていただいた書籍をご紹介します。
■機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック〜
この書籍は機械学習を解釈する手法としてPFI、PD、ICE、SHAPの大きく4つについて解説している書籍になります。
私が読んだ所感ですが、線形回帰の説明から始まり、機械学習モデルの解釈の必要性や目的に応じた手法が順序立てて説明されており非常に読みやすかったです。
また、簡単なモデルを例としていたため、数学的に躓く箇所もほとんどありませんでした。
さらに、Pythonコードも公開されているので、学んだ内容をすぐに実践できるのもオススメできるポイントです。
もしご興味ある方がいましたら購入を検討されてはいかがでしょうか?
終わりに
以上が、SHAPによる機械学習モデルの解釈法の説明となります。SHAPは予測値に対する特徴量の貢献度を可視化することで、なぜその予測値になったのかを説明できます。しかし、それだけでなく、データ全体から特徴量重要度や貢献度の分布、PDプロットなど様々な尺度で解釈することが可能でとても便利ですよね。簡単ではありましたが、、機械学習の解釈方法、SHAPへの理解について皆様の一助になれば幸いです。