こんにちは!ぼりたそです!
今回は機械学習モデルの解釈手法とその比較についてまとめた記事を作成しました。
以前、機械学習モデルの解釈手法として「PFI」、「PD」、「ICE」、「SHAP」について解説しましたが、それぞれの手法を比較して特徴や使い所などを整理してみました。
また、この記事のポイントは以下の通りです。
- 機械学習モデルの解釈手法
- PFI(Permutation Feature Importance)
- PD(Partial Dependence)
- ICE(Individual Conditional Expectation)
- SHAP(SHapley additive exPlanations)
- 参考書籍
それでは順に解説していきます。
機械学習モデルの解釈手法
機械学習モデルはほとんどの場合がブラックボックスとなってしまい、なぜその予測値になったのか?どの変数が影響しているか?などの情報が得られません。
そのため、重要な判断を下す際に何か根拠がないと困ってしまいます。
そこで、機械学習モデルを解釈する、つまりホワイトボックス化することを目的とした手法についていくつかご紹介します。
今回は「PFI」、「PD」、「ICE」、「SHAP」の4つの手法について解説していきます。
4つの手法について下にざっくりと比較表を作成しました。
| 項目 | PFI | PD | ICE | SHAP |
|---|---|---|---|---|
| 特徴 | モデル全体の特徴量重要度の手軽な評価 | 特徴量の全体的な影響や傾向の確認 | 個別データで特徴量の挙動を詳細に分析 | 予測値における特徴量の影響を分析 |
| メリット | モデルに依存せずに使用可能 | 徴量とターゲットの平均的関係を視覚化 | 交互作用を考慮して特徴量の影響を可視化 | ローカルとグローバルの両視点で解釈可能 |
| デメリット | 特徴量同士の相関に影響を受けやすい | 交互作用を考慮できない | 解釈が複雑になりやすい | 計算コストが高い |
それぞれの手法ごとに特徴を理解し、解釈したい対象に合わせて使い分けられるのが理想です。
それでは以下、順に説明していきます。
PFI(Permutation Feature Importance)
まずは特徴量重要度を算出する手法としてPFIについて解説していきたいと思います。
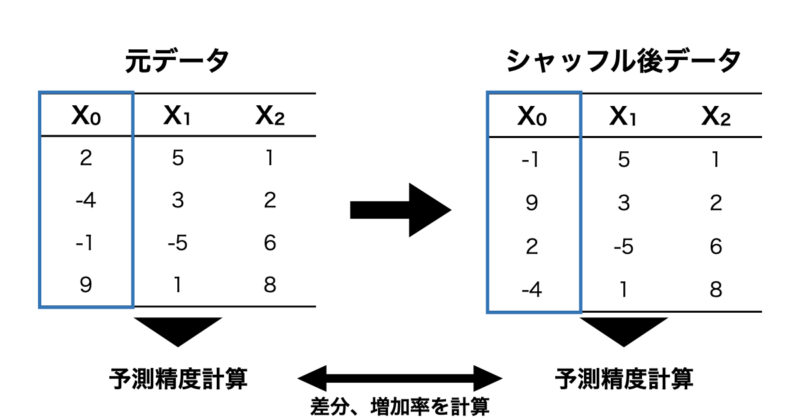
PFIは元のデータに対して特徴量をシャッフルしてその特徴量を使用できない状態にします。その状態で予測モデルを構築し、元データの予測精度と比較することで、その特徴量がどれだけ重要であったかを数値化する手法です。
実際に例を用いて説明していきます。
簡単な例として下のような $X = (X_0, X_1, X_2)$ を特徴量とした線形回帰式に従うデータを取り扱ってみます。
$$Y = 0 \cdot X_0 + 1 \cdot X_1 + 2 \cdot X_2$$
この線形回帰式のデータに対して以下の手順で特徴量重要度を算出します。
- まず、元データについて学習モデルを構築し、テストデータの予測誤差を計算します。
- 次に $X_0$ をシャッフルし、そのデータで予測モデルを構築した後にテストデータの予測誤差を算出します。
- 1の予測誤差に対して 2で算出した予測誤差を比較し、差分や増加率から特徴量重要度を計算する。
- $X_1$, $X_2$ も同様に1-3の手順を繰り返す。
実際にPythonを使用して算出してみます。
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.inspection import permutation_importance
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# 1. データ生成
np.random.seed(0)
n_samples = 100
X = np.random.rand(n_samples, 3)
y = 0 * X[:, 0] + 1 * X[:, 1] + 2 * X[:, 2] # f(x) = 0X_0 + 1X_1 + 2X_2
# 2. 学習データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 3. データの標準化(学習データに基づいて標準化)
scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.transform(X_test)
# 4. モデルの学習
model = LinearRegression()
model.fit(X_train_std, y_train)
# 5. テストデータを用いた PFI による特徴量重要度の計算
result = permutation_importance(model, X_test_std, y_test, n_repeats=30, random_state=0)
importance = result.importances_mean
# 6. 結果の可視化
feature_names = ['X_0', 'X_1', 'X_2']
importance_df = pd.DataFrame(importance, index=feature_names, columns=['Importance'])
importance_df.sort_values(by="Importance", ascending=True, inplace=True)
plt.figure(figsize=(8, 5))
plt.barh(importance_df.index, importance_df['Importance'], color='skyblue')
plt.xlabel("Feature Importance (PFI)")
plt.ylabel("Features")
plt.title("Permutation Feature Importance")
plt.show()
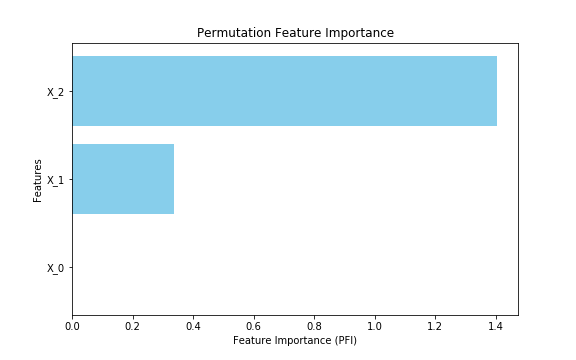
上記コードを実行すると以下のように特徴量重要度が計算されました。 $X_2$ が最も重要度が高く、次いで $X_1$ 、 $X_0$ は重要度がほぼ0になっています。元にした線形回帰の式からも妥当な結果であることがわかります。
ここまでPFIの説明をしてきましたが、PFIを使用するメリット、デメリットを以下にまとめます。
■メリット
■デメリット
以上がPFIの概要となりますが、より詳細な内容については以下の記事を参考にしていただければと思います。
PD(Partial Dependence)
次に特徴量と予測値の平均的な関係を理解する手法としてPD(Partial Dependence)について紹介していきます。
PDとは一言で説明すると「興味のある特徴量を動かし、他の特徴量を固定することで各インスタンス(個別データ)の予測値を平均して可視化する」手法です。
例えば、 $f(X_0, X_1, X_2)$ で表すことのできるモデルを構築した時、 $X_0$ と予測値の関係を可視化したいとします。
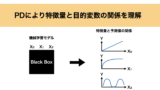
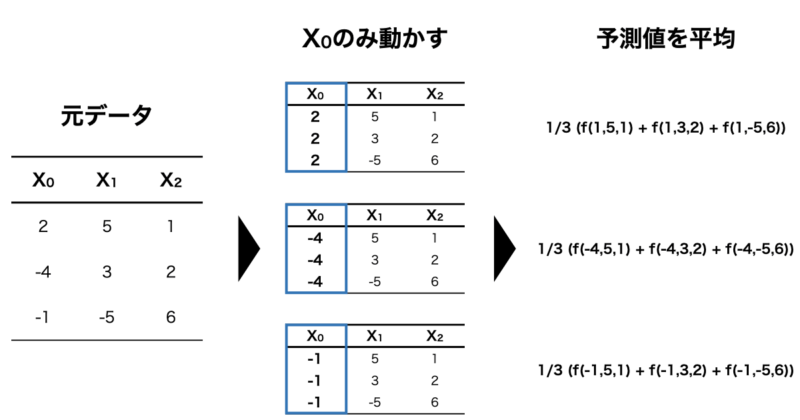
その場合、下の図のように $X_1, X_2$ の値は固定し、 $X_0$ の値のみを動かして予測値を算出します。
さらに、算出した予測値をインスタンスごとに平均化することで $X_0$ と予測値の関係を可視化することができるというわけです。

それでは実際にPythonを使用してPDを実行してみましょう。
今回は例として $X = (X_0, X_1, X_2)$ とした時、以下の $f(X)$ に従うデータを生成してPDを実行してみます。
$$f(X) = X_0 + \exp (- X_1 ) + sin( X_2 )$$
また、今回の機械学習モデルはランダムフォレストを使用し、説明変数は-5 ~ 5の範囲でデータを生成しています。
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.inspection import partial_dependence, PartialDependenceDisplay
import matplotlib.pyplot as plt
# データ生成
np.random.seed(42)
n_samples = 1000
X0 = np.random.uniform(-5, 5, n_samples)
X1 = np.random.uniform(-5, 5, n_samples)
X2 = np.random.uniform(-5, 5, n_samples)
y = X0 + np.exp(-X1) + np.sin(X2) + np.random.normal(0, 0.1, n_samples) # ノイズを追加
# DataFrame作成
X = pd.DataFrame({'X0': X0, 'X1': X1, 'X2': X2})
# ランダムフォレストモデルの構築
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X, y)
# absモデルのR2値を算出
y_pred = model.predict(X)
r2 = r2_score(y, y_pred)
print(f'Model R2 score: {r2:.4f}')
# Partial Dependence Plot
features = [0, 1, 2] # X0, X1, X2を指定
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
# 各特徴量ごとにPDプロットを描画
for i, feature in enumerate(features):
display = PartialDependenceDisplay.from_estimator(
model, X, [feature], ax=axes[i], line_kw={"color": "blue"}
)
axes[i].set_title(f'Partial Dependence Plot for X{feature}')
plt.suptitle("Partial Dependence Plots for Each Feature", fontsize=16)
plt.tight_layout()
plt.subplots_adjust(top=0.85)
plt.show()
#Model R2 score: 0.9998コードの実行結果として、まずは学習モデルの $R^2$ 値が1.0 となっており、きちんと学習できていることがわかります。
PDの実行結果は以下の通りです。左から $X_0, X_1, X_2$ となっており、生成元になった関数である$f(X) = X_0 + \exp ( X_1 ) + sin( X_2 )$からきちんと各特徴量と予測値の関係が可視化されていることがわかると思います。
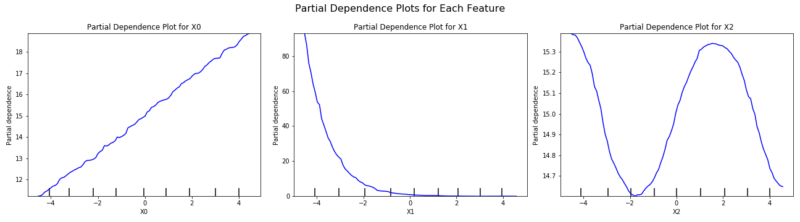

また、PDについて特徴量と目的変数の散布図と変わらないのでは?と思う方もいるかと思いますが、PDは全ての特徴量を考慮した上である特徴量と予測値の関係を可視化しているので、ただの特徴量VS目的変数の散布図とは全く異なります。
ここまでPDについて説明しましたが、PDを使用する具体的なメリット、デメリットについて以下にまとめます。
■メリット
■デメリット
以上がPDの説明となりますが、詳細な説明については以下の記事を参考にしていただけますと幸いです。
ICE(Individual Conditional Expectation)
次にICEについて説明していきます。
ICEとは一言で説明すると「興味のある特徴量を動かし、他の特徴量を固定することで予測値との関係を各データ(インスタンス)ごとに可視化する」手法です。
例えば、 $f(X_0, X_1, X_2)$ で表すことのできるモデルを構築した時、 $X_0$ と予測値の関係を可視化したいとします。
その場合、 $X_1, X_2$ の値は固定し、 $X_0$ の値のみを動かして予測値を算出します。
この時の特徴量と予測値の関係をインスタンスごとに可視化する手法がICEになります。
PDと似た手法になっていますが、ICEは興味のある特徴量以外を固定して予測値との関係をインスタンス(各データ)ごとに可視化し、PDはインスタンス全体を平均化してから可視化しています。
わかりやすくICEとPDの違いを下の図に示します。
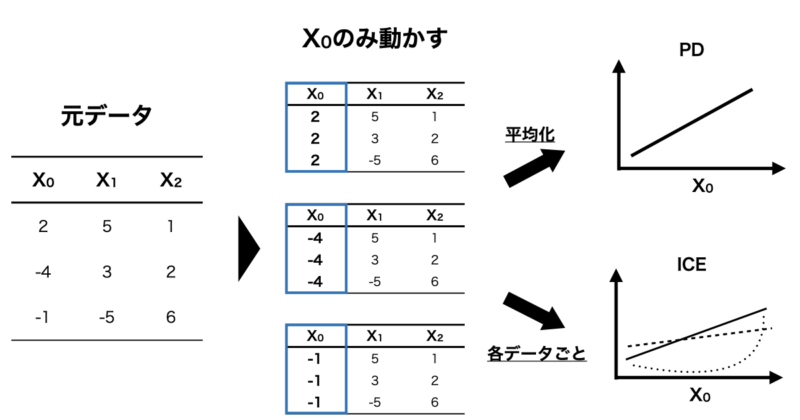

では、ICEとPDはどのように使い分ければいいのでしょうか?
PDのように平均化した方が全体としての特徴量と予測値の関係が捉えられていいのでは?と思いますが、一つ落とし穴があります。
それは特徴量間で交互作用がある場合です。
特徴量間に交互作用がある場合について、実際にICEとPDを実行することで理解を深めていきます。
今回は例として $X = (X_1, X_2)$ とした時、以下の $f(X)$ に従うデータを生成してPDを実行してみます。
$$f(X) = \sin ( X_1 ) \cos( X_2 )$$
この関数は $X_1$ , $X_2$ の間に交互作用があり、 $X_1$ に対する $f(X)$ のグラフは以下のようになっており、 $X_2$ の値によって正負が反転するインスタンスも存在する設定になっています。
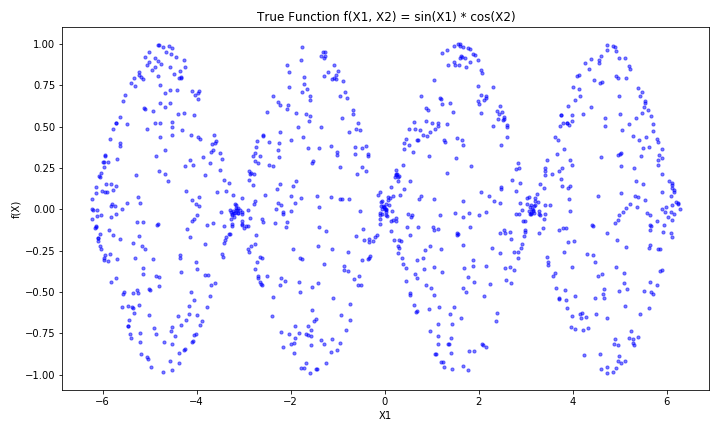

また、今回の機械学習モデルはランダムフォレスト回帰を使用しており、 $X$ の範囲は $-2 \pi < X < 2 \pi$ としています。
使用したPythonコードは以下の通りとなります。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.inspection import PartialDependenceDisplay
from sklearn.model_selection import train_test_split
# データ作成
np.random.seed(42)
n_samples = 1000
X1 = np.random.uniform(-2 * np.pi, 2 * np.pi, n_samples) # 変数 x を X1 に変更
X2 = np.random.uniform(-2 * np.pi, 2 * np.pi, n_samples) # 変数 y を X2 に変更
X = np.column_stack([X1, X2]) # X1, X2 を使って特徴量行列 X を作成
# 真の関数 f(X1, X2) = sin(X1) * cos(X2) + ノイズ
f_true = np.sin(X1) * np.cos(X2)
noise = np.random.normal(0, 0.1, n_samples) # ノイズを加える
target = f_true + noise
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, target, test_size=0.2, random_state=42)
# モデルの学習 (Random Forest Regressor)
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 特徴量インデックス (0: X1, 1: X2)
feature_index = 0 # X1 に対する PD と ICE を計算
# 部分依存プロット (PD) と ICE の計算とプロット
fig, ax = plt.subplots(figsize=(10, 6))
# ICE プロット (包括的に計算)
PartialDependenceDisplay.from_estimator(
model, X_test, features=[feature_index], kind='both', ax=ax, grid_resolution=50
)
plt.tight_layout()
plt.show()
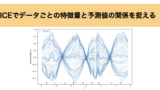
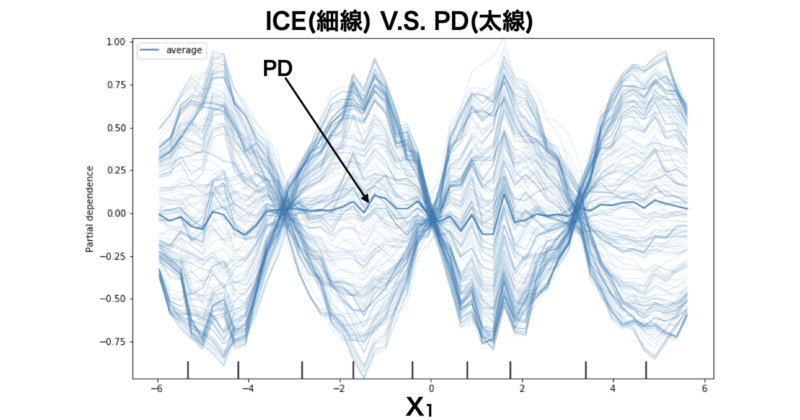
実行結果は以下の通りとなっており、 $X_1$ に対して予測値の関係をPDおよびICEで可視化しています。
見辛くて申し訳ないのですが、グラフ中の無数の細い青線がICEの結果、太線がPDの結果を表しています。
これを見ると、ICEは各インスタンスごとに特徴量 $X_1$ と予測値の関係を可視化しているので、 $X_1$ , $X_2$ の交互作用をきちんと表現できています。
一方、PDはインスタンスを全体で平均化してしまうため、ほぼ0で推移しており、特徴量と予測値の関係が表現できていないことがわかります。

ここまでICEについて説明してきましたが、ICEを使用する具体的なメリット、デメリットについて以下にまとめます。
■メリット
■デメリット
以上がICEの説明になりますが、詳細について知りたい方は以下の記事を参考にしていただけますと幸いです。
SHAP(SHapley additive exPlanations)
最後に機械学習がなぜその予測値を出したのかを解釈するSHAP(SHpley Additive exPlanations)という手法について説明していきます。
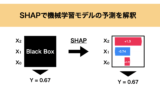
SHAPは下の図のように機械学習で出された予測に対して、特徴量の寄与などを算出することで各特徴量がどのように影響しその予測値に至ったのかを解釈することができます。
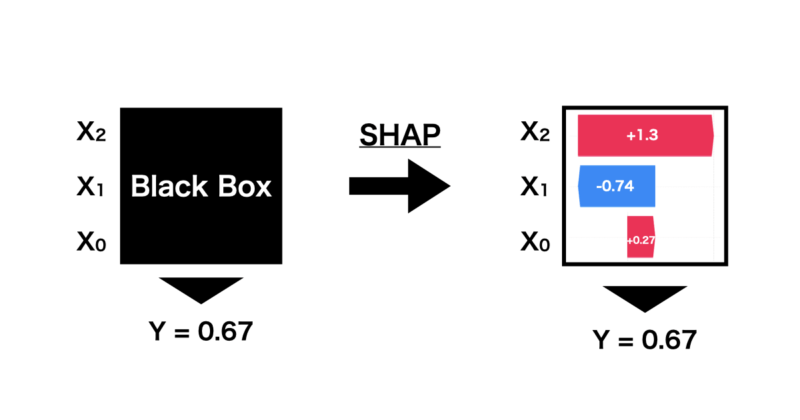

この貢献度は協力ゲーム理論に基づいたShapley値を応用して計算しています。詳細は後に紹介する記事から参照いただければと思います。
ひとまず、実際にSHAPを実行していきます。
今回は例として $X = (X_0, X_1, X_2)$ としたとき、以下の $f(X)$ に従うデータを生成します。
$$f(X) = X_0\ -\ 4^{X_1} + \exp ( X_2)$$
生成したデータに対してランダムフォレスト回帰を行い、予測した1点に対してSHAPを実行してみました。
import numpy as np
import pandas as pd
import shap
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
# 訓練用データの生成
np.random.seed(0)
X_train = pd.DataFrame({
'X0': np.random.uniform(-2, 2, 100),
'X1': np.random.uniform(-2, 2, 100),
'X2': np.random.uniform(-2, 2, 100)
})
# ターゲット変数の計算
y_train = X_train['X0'] - 4**(X_train['X1']) + np.exp(-X_train['X2'])
# モデルの訓練
model = RandomForestRegressor(n_estimators=100, random_state=0)
model.fit(X_train, y_train)
# 予測用データの生成(ランダムに1点)
X_test = pd.DataFrame({
'X0': np.random.uniform(-2, 2, 1),
'X1': np.random.uniform(-2, 2, 1),
'X2': np.random.uniform(-2, 2, 1)
})
# SHAPの値を計算
explainer = shap.TreeExplainer(model)
shap_values_test = explainer.shap_values(X_test)
# グラフの表示(Waterfall Plot)
for i in range(1): # 予測用データの1点を表示
shap.waterfall_plot(shap.Explanation(values=shap_values_test[i], base_values=explainer.expected_value, data=X_test.iloc[i]))
出力結果が以下の通りとなります。下のグラフはwaterfall plotと言って縦軸に特徴量とその値、横軸には予測した $f(X)$ に対する特徴量の貢献度が可視化されています。
今回は $X_0 = 1.626$ , $X_1 = 1.096$ , $X_2 = -0.667$ に対して予測値が $f(X) = -0.484$ となっており、この時の特徴量の貢献度が示されています。
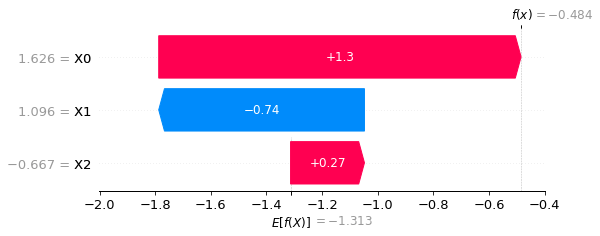

なお、$E[f(X)]$ は予測値の平均的な期待値であり、ベースラインくらいの認識で問題ありません。このベースラインから各特徴量の貢献度を足し合わせることで予測値が算出されるようになっています。
また、SHAPは一つの予測点における特徴量の貢献度を算出していますが、これを全てのデータで行い、平均化することでデータ全体における特徴量重要度として可視化することができます。
SHAPの実行にて紹介したコードに以下のコマンドを追加することでデータ全体から見た特徴量重要度をグラフ化することができます。
# 1. Bar Plotの可視化
shap.summary_plot(shap_values, X, plot_type="bar")実行結果は以下の通りです。縦軸が特徴量となっており、横軸がその重要度を示しています。
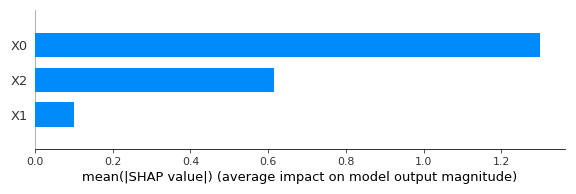

SHAPはミクロな視点で予測点における特徴量の貢献度を算出できるだけではなく、マクロな視点で特徴量重要度を算出できるため、使い勝手が非常に良いです。
ここまでSHAPについて説明してきましたが、SHAPを使用することによる具体的なメリット、デメリットを以下にまとめます。
■メリット
■デメリット
以上がSHAPの説明になりますが、詳細について知りたい方は以下の記事を参考にしていただけますと幸いです。
参考書籍
本記事を作成するにあたり参考にさせていただいた書籍をご紹介します。
■機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック〜
この書籍は機械学習を解釈する手法としてPFI、PD、ICE、SHAPの大きく4つについて解説している書籍になります。
私が読んだ所感ですが、線形回帰の説明から始まり、機械学習モデルの解釈の必要性や目的に応じた手法が順序立てて説明されており非常に読みやすかったです。
また、簡単なモデルを例としていたため、数学的に躓く箇所もほとんどありませんでした。
さらに、Pythonコードも公開されているので、学んだ内容をすぐに実践できるのもオススメできるポイントです。
もしご興味ある方がいましたら購入を検討されてはいかがでしょうか?
終わりに
以上が機械学習モデルの解釈手法に関する説明となります。特に仕事で機械学習を使う際は解釈性も重要になってくると思います。実験が高いなど重要な局面であるほど根拠が必要になってくるので、その際に今回紹介した手法が役立てば幸いです。