こんにちは!ぼりたそです!
今回はデータの前処理や可視化の際に使用する次元削減法について3つの手法をまとめてみました。
この記事は以下の要点でまとめています。
- 次元削減法とは?
- 主な次元削減手法
- Pythonで実行
それでは順に解説していきます。
次元削減法とは?
次元削減とは、「データの持つ情報をできるだけ維持しながら、次元(特徴量の数)を減らすこと」です。
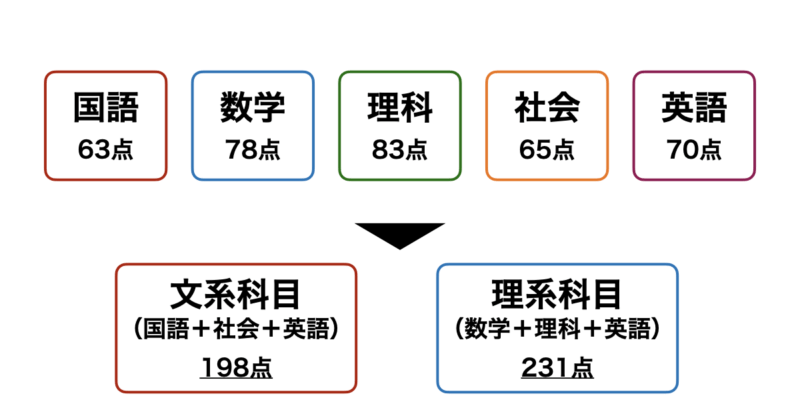
例えば、下図のように「国語」、「数学」、「理科」、「社会」、「英語」の5科目のテストのスコアデータがあるとします。
これを理系科目=「数学」+「理科」+「英語」、文系科目=「国語」+「社会」+「英語」とすることで5次元あったデータを二次元に圧縮することができます。この次元削減によりこの生徒はざっくり理系科目が得意な傾向にあることがわかります。
ではなぜ次元削減をする必要があるのか?その理由はいくつかあります。
- 計算コストの削減
- 特徴量の数が多いと、機械学習モデルの学習に時間がかかります。そのため、次元削減を行うことで計算量を減らし、処理を高速化できます。
- データの可視化
- 人間は2次元や3次元のデータは直感的に理解できますが、100次元や1000次元のデータは理解できません。そのため、次元削減を使って2次元や3次元に圧縮することで、データの分布やパターンを視覚的に確認できます。
- ノイズ除去と特徴抽出
- データには不要な特徴(ノイズ)が含まれていることが多いです。そのため、次元削減を行うことで重要な情報を保持しつつ、ノイズを除去できます。
主な次元削減手法
次に主な次元削減手法について説明していきます。
今回はよく使用される手法として主成分分析(PCA)、t-SNE、UMAPをご紹介します。
はじめに3つの手法について強み、弱み、使用場面についてまとめてみました。
| 手法 | 強み | 弱み | 使用場面 |
|---|---|---|---|
| PCA | ・線形情報の保持 ・計算が速い | ・非線形情報が捉えられない ・クラスタが重なりがち | ・前処理 ・特徴量選択 ・全体構造の把握 |
| t-SNE | ・局所構造の保持 ・クラスタの明確な分離 | ・計算が遅い ・大域構造が歪む | ・クラスタの可視化 ・類似データの探索 |
| UMAP | ・局所/大域構造のバランス ・高速な計算 | ・ハイパーパラメータ調整が難しい | ・大規模データの可視化 ・クラスタリングの補助 |
- PCA(Principal Component Analysis)
PCAの強みとしては計算が速く、次元圧縮後も線形情報を保持できる点が挙げられます。一方で非線形情報は捉えることが難しく、二次元に圧縮した際にクラスターが重なりがちな傾向がある欠点があります。主な使用場面としては特徴量選択による変数削減などが挙げられます。
- t-SNE(t-Distributed Stochastic Neighbor Embedding)
t-SNEの強みは高次元におけるデータの局所構造(近いデータ同士の距離)を低次元でも保持できることです。これにより、次元圧縮した際もクラスターが重ならず明確な分離が可能となります。一方でデータ間の距離が大きいと次元圧縮後まで構造を保持することが難しく、またデータ量が多いと計算量が遅いという欠点があります。主な使用場面としては次元圧縮によるクラスタの可視化や類似データの探索などが挙げられます。
- UMAP(Uniform Manifold Approximation and Projection)
UMAPの強みは計算が高速であるにも関わらず、高次元におけるデータの局所構造(近いデータ間の距離)/大局構造(遠いデータ間の距離)を低次元でも保持できることです。t-SNEの欠点を克服した手法でもあります。一方でハイパーパラメータと呼ばれるあらかじめ設定が必要なパラメータが多く、調整が難しいという欠点もあります。主な使用場面は大規模データの可視化などが挙げられます。
各手法の特徴について簡単に説明しましたが、それぞれのアルゴリズムも解説していきます。
PCA(主成分分析)
主成分分析(PCA)は、多くの変数を持つデータを、より少ない数の「主成分」と呼ばれる新しい変数に変換して、データの線形情報を保ちながら、簡潔に次元削減することができます。
まず、例として標準化した2変数(X1,X2)データが以下のような二次元グラフで表せるとします。
ここで、データの分散が最大となる方向(軸)を探します。これが、新しい基準軸「主成分」になります。
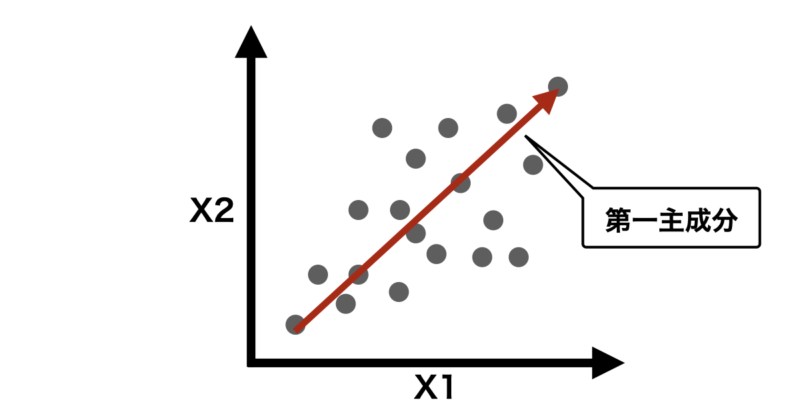
PCAでは第二主成分以降も同様に計算します。下の説明のように第一主成分以降はそれ以前の主成分に直行するように生成されます。
主成分同士が直行することは互いに独立であることを示し、異なる情報を持った軸になることを意味します。逆にほとんど同じ方向の主成分は同じような情報しか表現することができず、あまり意味がないことになります。
- 第1主成分 (PC1):データの分散が最大になる方向を表し、最も多くの分散を説明します。
- 第2主成分 (PC2):第1主成分に直交する(90度の角度で独立している)方向で、残りの分散を最大限に説明します。
- 以降の主成分:それぞれ前の主成分に直交する方向で、データの分散を説明する順番に計算されます。
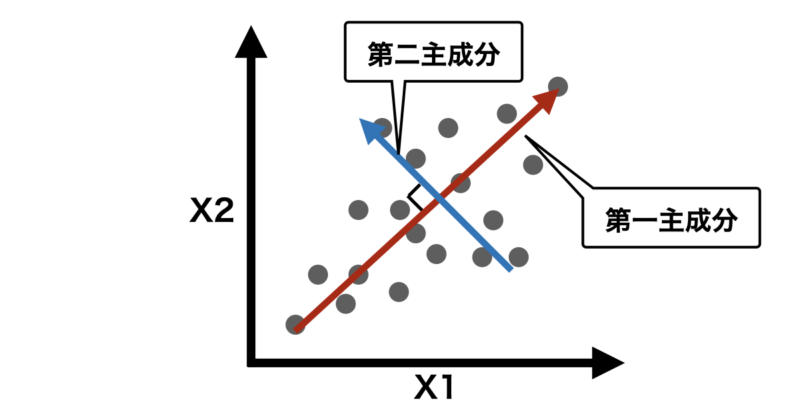
このように第一〜第n主成分までを計算し、任意の主成分を選択したら後はその主成分を基にデータを反映すればPCAは完了です。
PCAについてより詳しく知りたい方は以下の記事を参照いただければと思います。
t-SNE
t-SNEは高次元空間 でのデータ点の距離感 を低次元空間 にそのまま保つ。つまり、「近い点は近くに、遠い点は遠くに」 を目指すことを目的としています。
これを実現するアルゴリズムとして以下のような手順で処理しています。
- 高次元空間におけるデータの近さを定義
データ点 $x_1, x_2, …, x_n$を考えるとき、それぞれのデータ点がガウス分布に従うと仮定します。
このとき、データ点 $x_i$ と $x_j$の距離は以下の条件付き確率分布として表します。
$$p_{j|i} = \frac{\exp\left(-\frac{| x_i – x_j |^2}{2 \sigma_i^2}\right)}{\sum_{k \neq i} \exp\left(-\frac{| x_i – x_k |^2}{2 \sigma_i^2}\right)}$$
$\sigma_i$ はスケールパラメータ(バンド幅)
また、上の条件付き確率を対称化するために $p_{j|i}$ と $p_{i|j}$ の平均 を取って、対称な確率 $P_{ij}$ を定義し、これを高次元空間におけるデータの近さとします。
$$P_{ij} = \frac{p_{j|i} + p_{i|j}}{2N}$$
- 低次元空間におけるデータの近さを定義
低次元に変換したデータ点 $y_1, y_2, …, y_n$を考えるとき、それぞれのデータ点がt分布に従うと仮定します。
このとき、データ点 $y_i$ と $y_j$の距離は以下の確率分布$Q_{ij}$として表し、これを低次元におけるデータの近さとして定義します。
$$Q_{ij} = \frac{\left( 1 + | y_i – y_j |^2 \right)^{-1}}{\sum_{k \neq l} \left( 1 + | y_k – y_l |^2 \right)^{-1}}$$
- コスト関数を定義
高次元の確率 $P_{ij}$ と 低次元の確率 $Q_{ij}$ の差異をKLダイバージェンスを使用したコスト関数 $C$ として定義します。
KLダイバージェンスは、2つの確率分布の間の違いを測る指標です。簡単に言うと、ある確率分布 $P$ が、もう一方の確率分布 $Q$ にどれだけ「似ていないか」を表す指標です。
$$C = \sum_{i \neq j} P_{ij} \log \frac{P_{ij}}{Q_{ij}}$$
- コスト関数の最小化
コスト関数 $C$ を最小化するためには勾配降下法 を使用します。
勾配降下法は、関数の最小値を見つけるための手法です。具体的には、関数の勾配(傾き)を利用して、関数の値が減少する方向にパラメータを更新していきます。
勾配の計算:
$$\frac{\partial C}{\partial y_i} = 4 \sum_{j \neq i} \left( P_{ij} – Q_{ij} \right) \left( y_i – y_j \right) \left( 1 + | y_i – y_j |^2 \right)^{-1}$$
計算した勾配から以下の式に従って $y_i$ を更新していきます。
$$y_i \leftarrow y_i – \eta \frac{\partial C}{\partial y_i}$$
$\eta$ は学習率であり勾配に対してどれだけ進むかを表している。
このとき、$P_{ij} > Q_{ij}$ のとき、 $y_i$ を近づけるように更新し、$P_{ij} < Q_{ij}$ のとき、 $y_i$ を遠ざけるように更新します。
以上のアルゴリズムから高次元空間 でのデータ点の距離感 を低次元空間 にそのまま保つような次元削減を行うことができます。
t-SNEに関してより詳しく知りたい方がいれば以下の記事を参照いただければと思います。
UMAP
UMAPの目的もt-SNEと同じように、高次元データを低次元に圧縮しながら、データの構造や関係性をできるだけ保つことです。
これにより、視覚的にデータの分布を理解しやすくしたり、クラスタ構造を発見したりできます。
これを実現するために以下のステップで次元圧縮を行います。
- 高次元における確率近傍モデルの構築
UMAPは、高次元空間でのデータ点同士の類似性を表すために 近傍グラフ(k-NN グラフ) を構築します。具体的には、データ点 $x_i$ の近傍点集合を考え、確率的に重み付けされたグラフ を作成します。
実際には以下の式で定義されます。
$$p_{ij} = \exp\left( \frac{-d(x_i, x_j) – \rho_i}{\sigma_i} \right)$$
$d(x_i,x_j)$ は $x_i$ と $x_j$ の距離。通常はユークリッド距離を使用。
$\rho_i$ はn_neighbors 個目の「最も近い点との距離」
$\sigma_i$ はスケールパラメータ(適応的に決定)
n_neighbors はハイパーパラメータであり、この値が大きければデータがより大局的構造を強調し、小さければ局所構造(クラスター)を強調する傾向があります。
また、上の条件付き確率を対称化した確率 $P_{ij}$ を定義し、これを高次元空間におけるデータの近さとします。
$$P_{ij} = p_{ij} + p_{ji} – p_{ij} p_{ji}$$
- 低次元における確率モデルの構築
次に低次元空間でも、高次元で得られた近傍関係を再現するような確率分布を構築していきます。
具体的にUMAPでは、双曲線相関関数を用いて、低次元空間での確率を以下の式で定義します。
$$q_{ij} = \left( 1 + a d(y_i, y_j)^{2b} \right)^{-1}$$
$d(y_i, y_j)$ は低次元空間におけるデータ点の距離関数。通常はユークリッド距離を使用。
$a, b$ はデータセットに応じて調整されるハイパーパラメータ
ちなみに$d(y_i, y_j)$が0にならないように最小距離(min_dist)を設定する必要があります。
これにより最適化時に距離がmin_dist以下にならないように調整されるため、データの局所構造を適度に維持しながらも、データの過度な密集を防ぎます。
- コスト関数の定義
次にコスト関数の定義を行います。
具体的にUMAPはコスト関数をクロスエントロピー損失として定義し、これを最小化することで高次元と低次元のデータ距離がなるべく一致するようにしています。
$$\mathcal{L} = \sum_{i \neq j} P_{ij} \log q_{ij} + (1 – P_{ij}) \log (1 – q_{ij})$$
式の説明として、
第1項:高次元で近い点($P_{ij}$ が大きい点)同士が、低次元でも近くなるようにする。
第2項:高次元で遠い点($P_{ij}$ が小さい点)同士が、低次元でも遠くなるようにする。
- コスト関数の最適化
確率的勾配降下法という手法を用いて最適化します。
確率的勾配降下法とは簡単に言えば、「コスト関数の値を小さくする方向へ少しずつパラメータを更新する」 方法で以下の式に従って更新します。
$$y_i^{(t+1)} = y_i^{(t)} – \eta \frac{\partial \mathcal{L}}{\partial y_i}$$
また、$\eta$ は学習率であり勾配に対してどれだけ進むかを表しています。大きすぎると最小値を過ぎてしまい解が収束せず、小さすぎると最小化まで膨大な時間がかかってしまいます。
以上のアルゴリズムから高次元データを低次元に圧縮しながら、データの構造や関係性をできるだけ保つことができます。
Pythonで実行
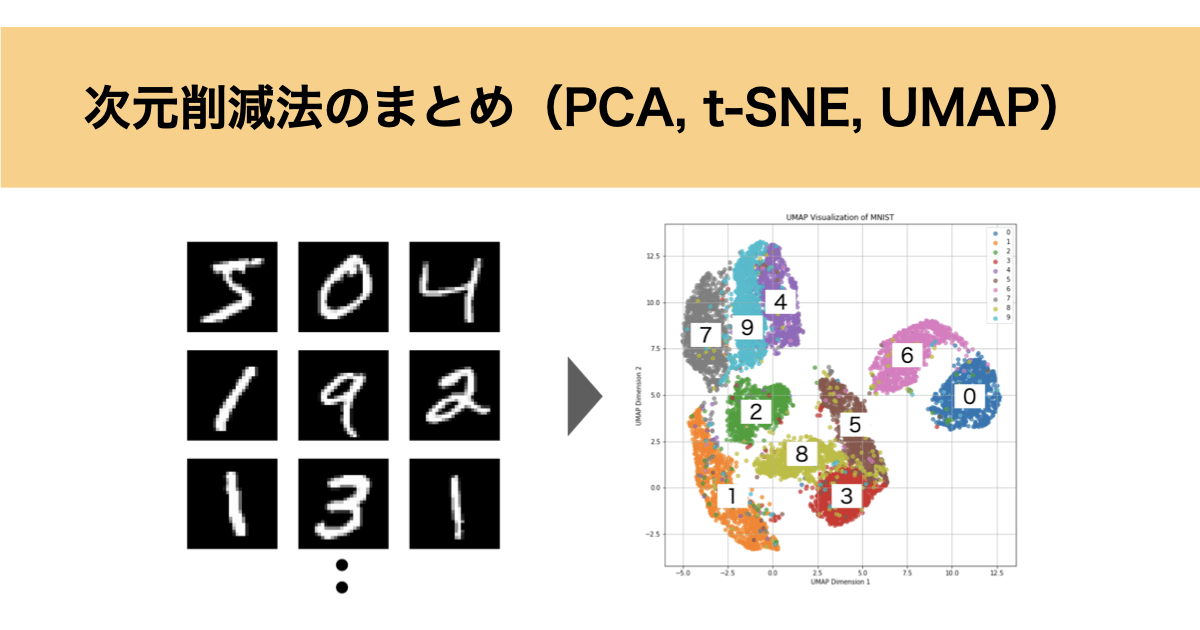
それでは、試しにPCA、t-SNE、UMAPについて手書き数字データ(MNIST)の次元削減を行なっていきます。
MNISTは下図のように28×28ビットの合計784ビットとして表され、各ビットは白から黒までの濃淡を表す0~255の数値が格納されています。
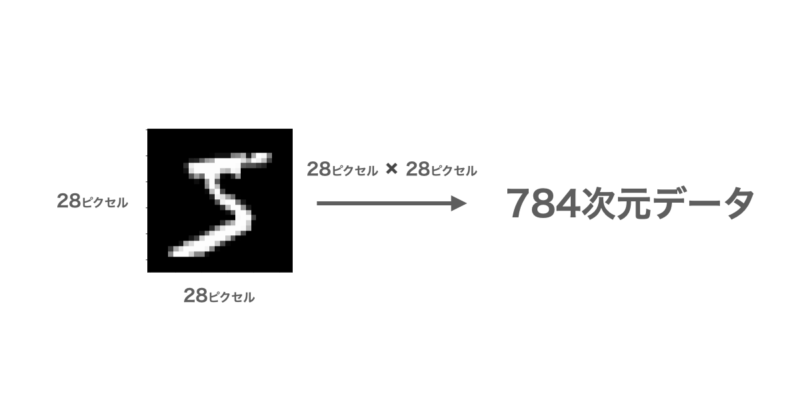

このMNISTが0~9の数字について10000個用意し、784次元のデータを2次元のグラフとして可視化したいと思います。
使用したコードは以下の通りです。
import numpy as np
import matplotlib.pyplot as plt
import umap
from sklearn.datasets import fetch_openml
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
# MNIST データセットのダウンロード
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
X = mnist.data
y = mnist.target.astype(int)
# 計算量削減のため、ランダムに 10000 件を抽出
np.random.seed(42)
indices = np.random.choice(X.shape[0], 10000, replace=False)
X_subset = X[indices]
y_subset = y[indices]
# --- PCA ---
pca_model = PCA(n_components=2, random_state=42)
X_pca = pca_model.fit_transform(X_subset)
# --- t-SNE ---
tsne_model = TSNE(n_components=2, perplexity=10, learning_rate=50, random_state=42)
X_tsne = tsne_model.fit_transform(X_subset)
# --- UMAP ---
umap_model = umap.UMAP(n_components=2, n_neighbors=10, min_dist=0.3, random_state=42)
X_umap = umap_model.fit_transform(X_subset)
# プロット関数
def plot_embedding(X_embedded, title):
plt.figure(figsize=(10, 10))
for i in range(10):
indices = y_subset == i
plt.scatter(X_embedded[indices, 0], X_embedded[indices, 1], label=str(i), alpha=0.7)
plt.legend()
plt.title(title)
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.grid(True)
plt.show()
# プロット
plot_embedding(X_pca, "PCA Visualization of MNIST")
plot_embedding(X_tsne, "t-SNE Visualization of MNIST")
plot_embedding(X_umap, "UMAP Visualization of MNIST")
では実行結果を順に見ていきます。
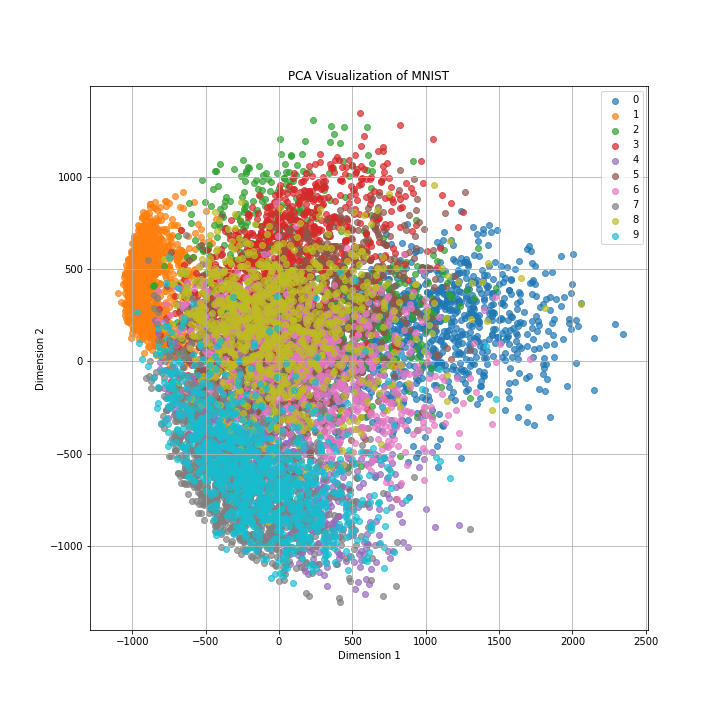
◼️PCA
なんとなく数字ごとにクラスターが形成されているように見えますが、クラスター同士が重なってしまっていますね。
PCAは非線形情報を保持するのが不得意であり、データによっては可視化がうまくいかないこともあります。一方で次元削減はデータの可視化以外にも特徴量選択などの用途もありますので、一概にPCAに魅力がないとは言えません。

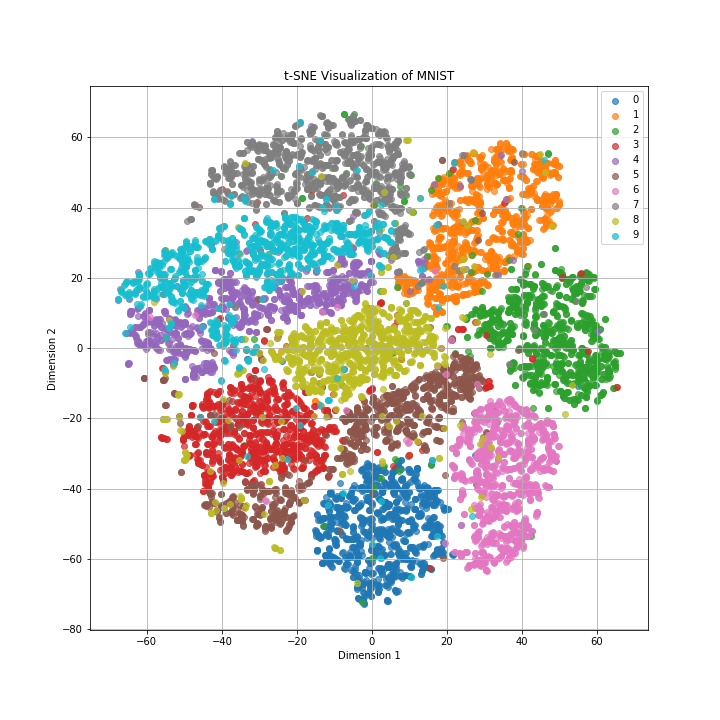
◼️t-SNE
数字ごとにクラスターが分けられており、クラスター同士が大きく重なっている様子もありません。
また、似たような数字の形をしている「4」、「7」、「9」や「3」、「8」、「5」はクラスター同士が近い傾向が読み取れます。

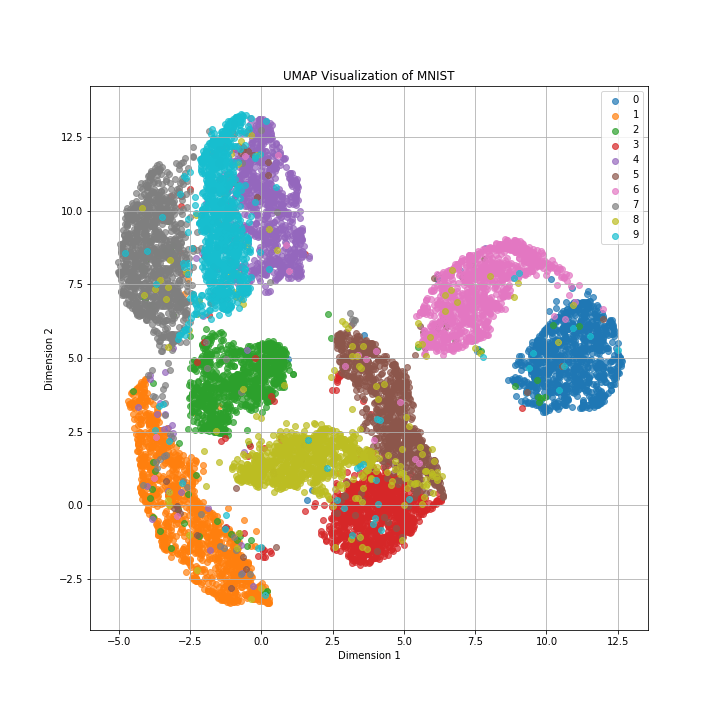
◼️UMAP
t-SNEと同様に数字ごとにクラスターが分けられており、クラスター同士が大きく重なっている様子もありません。
t-SNEと比較するとクラスターの密度が高く局所構造を保持できているだけでなく、似ていないクラスター同士は大きく離れており大局構造も保持できていることがわかります。
クラスターの可視化という点ではt-SNEより見やすいですね。

以上がPCA, t-SNE, UMAPにおけるMNISTの二次元マップの可視化をPythonで実行した結果になります。
終わりに
いかがでしたでしょうか。PCA, t-SNE, UMAPにはそれぞれ特徴があり、用途や扱うデータの性質により使い分けが必要になってきます。どれを使えばいいかわからない場合はそれぞれの手法を実行してみて比較するのが早いかと思います。また、次元削減法は今回紹介した3つの手法以外も存在しており、興味のある方は調べてみてもいいかもしれません。