こんにちは、ぼりたそです!
機械学習モデルを使っていて「もっと精度が上がらないかな?」と思ったことはありませんか?
その原因、もしかすると“ハイパーパラメータ”にあるかもしれません。
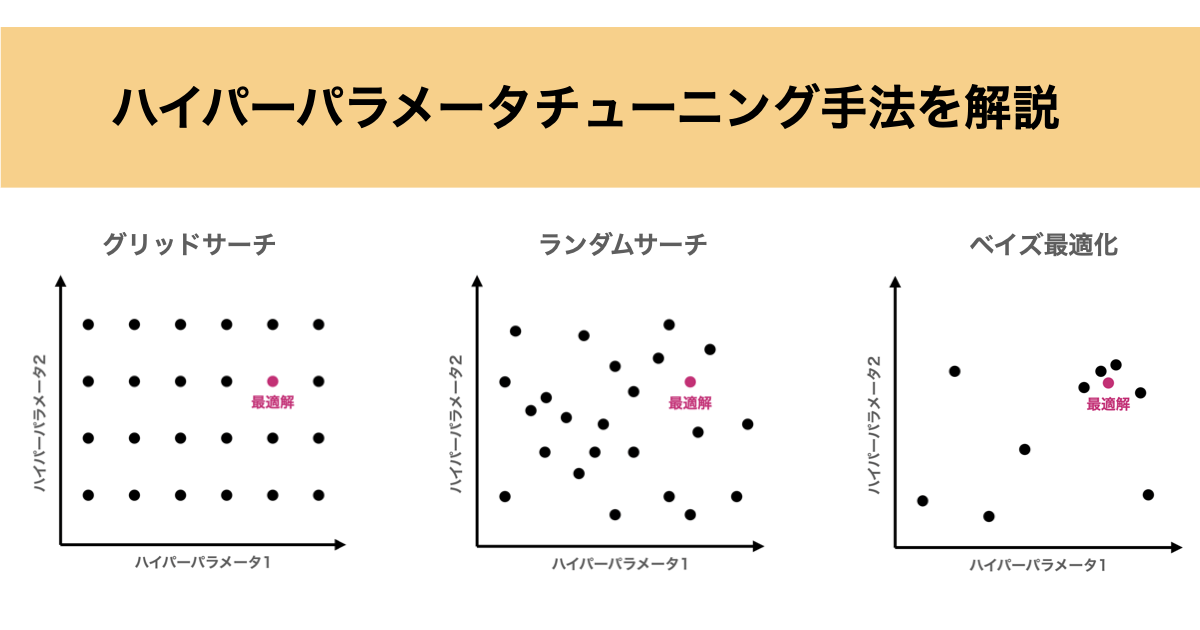
この記事では、モデルの精度に大きく影響を与える「ハイパーパラメータのチューニング方法」について、代表的な3つの手法を比較しながら解説します。
この記事では以下のポイントについて解説しています。
- ハイパーパラメータとは?
- ハイパーパラメータのチューニング手法
- チューニング手法の概要と特徴
- Pythonでの実装
ハイパーパラメータとは?
ハイパーパラメータとは、モデルの学習プロセスや構造を決める外部設定値です。これらはデータから自動的に学習されるのではなく、あらかじめ人間が指定する必要があります。(一部の機械学習モデルでは自動的に設定できる場合もあります)
ハイパーパラメータの例:
| モデル名 | ハイパーパラメータ例 |
|---|---|
| ランダムフォレスト | 決定木の本数、各木の最大の深さ、各木の最大特徴量数など |
| サポートベクターマシン(SVM) | 誤差許容度、カーネルのスケール長 |
| ニューラルネットワーク | 学習率、バッチサイズ、エポック数など |
このハイパーパラメータを調整しないと以下の問題が発生する可能性が高いです。
- 機械学習モデルの精度が低い(過学習や未学習)
- 汎化性能が低い
- 計算コストが無駄になる
そのため、モデル性能を最大限に引き出すためにはハイパーパラメータのチューニングは不可欠です。
ハイパーパラメータチューニングの手法一覧と比較
これからご紹介する手法はそれぞれ特長が異なり、「どのような場面でどの手法を使うべきか?」を理解することが重要です。
以下の表に、各手法の特徴を比較してまとめました。
| 手法名 | 探索方法 | 計算コスト | 向いている場面 |
|---|---|---|---|
| グリッドサーチ | すべてのパラメータの組み合わせを網羅的に試す | 高い | パラメータ数が少なく、計算資源に余裕があるとき |
| ランダムサーチ | パラメータ空間からランダムに組み合わせを抽出して試す | 中程度 | パラメータ数が多く、ざっくり良い結果を得たいとき |
| ベイズ最適化 | 過去の結果から次の試行を賢く選ぶ(予測モデルに基づく) | 低〜中 | 評価に時間がかかる/試行回数が限られるとき |
それぞれの手法には一長一短があるため、「どの手法が最適か?」は以下のように判断すると良いかと思います。
- 簡単なモデル・計算資源に余裕あり → グリッドサーチ
- パラメータが多く大まかに探索したい → ランダムサーチ
- 試行回数が少ない、1回の評価に時間がかかる → ベイズ最適化
このように、各チューニング手法には目的や状況に応じた「使いどころ」があります。次章では、これらの手法について概要と特徴を紹介していきます。
ハイパーパラメータのチューニング手法の概要と特徴
前章では、グリッドサーチ・ランダムサーチ・ベイズ最適化の特徴や使い分けについて、比較表を用いてざっくりと把握しました。
ここからは、さらに一歩踏み込んで、それぞれの手法が「どのようにパラメータを選び、試行しているのか」というアルゴリズムの仕組みについて解説していきます。
グリッドサーチ
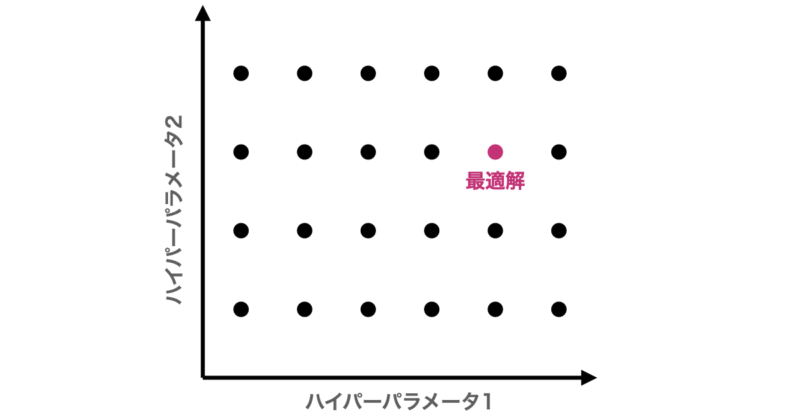
グリッドサーチは、指定したパラメータ範囲のすべての組み合わせを試す方法です。
最も単純で分かりやすく、確実性はありますが、パラメータ数が増えると組み合わせが爆発的に増え、計算コストが非常に高くなるという欠点があります。
ランダムサーチ
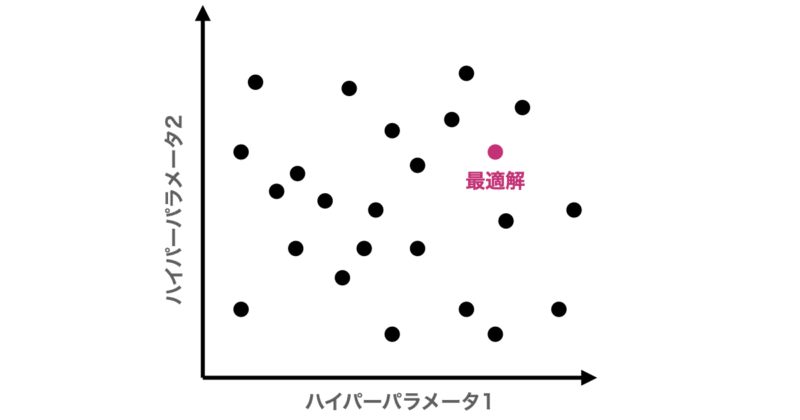
ランダムサーチは、指定した範囲内からランダムにパラメータの組み合わせを抽出して試す方法です。
全体のごく一部しか探索しませんが、実は効率が良い場合も多く、限られた試行回数で優れた性能にたどり着くことが可能です。
一方でランダムに抽出するため場合によっては最適なパラメータを逃す可能性があります。
ベイズ最適化
ベイズ最適化は、これまでに試した結果を元に「次に試すべきパラメータの候補」を推論する賢いチューニング手法です。具体的には、獲得関数(Expected Improvementなど)を最大化する点(期待できる点)を次の候補として選びます。
この手法は、特に「1回の学習に時間がかかるモデル」や「試行回数が限られるタスク」において、最小限の試行で高い精度を出すことが可能です。
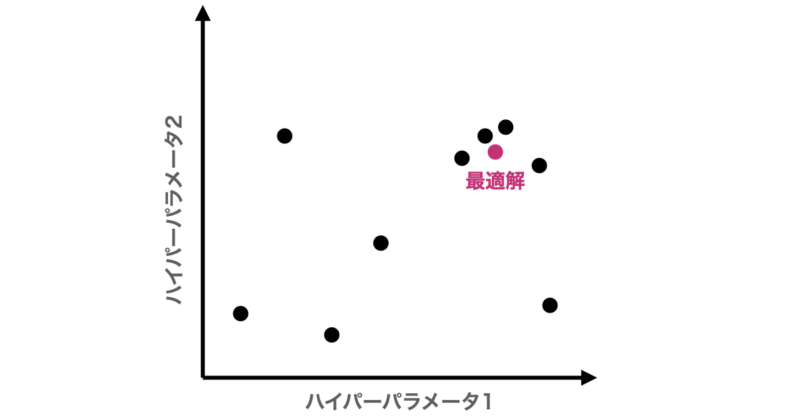
ベイズ最適化については以下の記事でまとめているので、興味のある方はご参考になさって下さい。
Pythonにて実装&比較
先ほど紹介した3つの手法についてPythonで実行して比較してみたいと思います。
今回紹介しているのはハイパーパラメータのチューニング手法ですが、本章ではその挙動をより直感的に理解するため、あえて「Booth関数の数値最適化問題」を取り扱っていきます。
Booth関数とは以下の式で表すことができ、図のように滑らかな曲線を持ち、最小値は$ f(1,3) = 0 $です。
$$
f(x, y) = (x + 2y – 7)^2 + (2x + y – 5)^2
$$
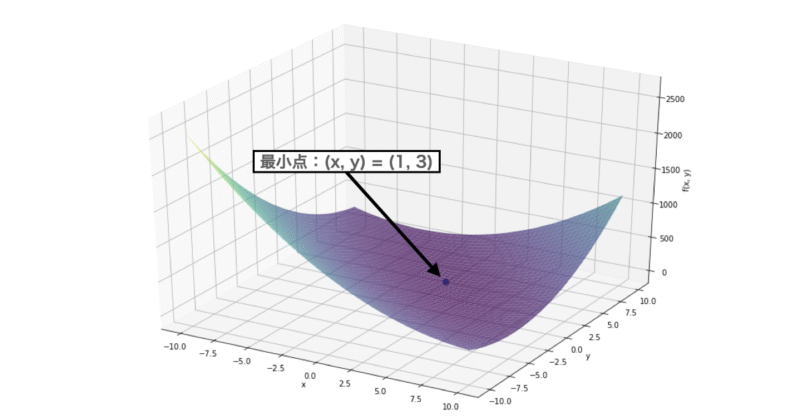

実装内容としては、まず探索空間を1000点に分割し各手法で $ (x, y) $ の組合わせを選ばせます。この時、最小値である$ (x,y) = (1,3) $が選ばれるまでの試行回数から探索効率について評価しました。
実際に使用したコードは以下の通りです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import ParameterGrid, ParameterSampler
import optuna
import pandas as pd
import logging
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings("ignore")
# ========= Booth関数 =========
def booth(x, y):
return (x + 2*y - 7)**2 + (2*x + y - 5)**2
# ========= 探索空間定義 =========
x_vals = np.linspace(-10, 10, 32)
y_vals = np.linspace(-10, 10, 32)
# 最適点 (1, 3) を確実に含める
x_vals[15] = 1.0
y_vals[23] = 3.0
param_grid = {'x': x_vals, 'y': y_vals}
all_candidates = list(ParameterGrid(param_grid)) # 32×32 = 1024点
n_trials = 1000
# ========= Grid Search =========
grid_results = [(p['x'], p['y'], booth(p['x'], p['y'])) for p in all_candidates[:n_trials]]
grid_best = min(grid_results, key=lambda x: x[2])
grid_best_index = next(i+1 for i, r in enumerate(grid_results) if r[0] == 1.0 and r[1] == 3.0)
# ========= Random Search =========
random_points = list(ParameterSampler(param_grid, n_iter=n_trials, random_state=42))
random_results = [(p['x'], p['y'], booth(p['x'], p['y'])) for p in random_points]
random_best = min(random_results, key=lambda x: x[2])
try:
random_best_index = next(i+1 for i, r in enumerate(random_results) if r[0] == 1.0 and r[1] == 3.0)
except StopIteration:
random_best_index = None
# ========= Bayesian Optimization =========
optuna.logging.set_verbosity(logging.WARNING) #Optuna:ログ抑制設定
def objective(trial):
x = trial.suggest_categorical("x", list(x_vals))
y = trial.suggest_categorical("y", list(y_vals))
return booth(x, y)
study = optuna.create_study(direction="minimize", sampler=optuna.samplers.TPESampler(seed=42))
study.optimize(objective, n_trials=n_trials)
bayes_best = (study.best_params["x"], study.best_params["y"], study.best_value)
try:
bayes_best_index = next(i+1 for i, t in enumerate(study.trials)
if t.params.get("x") == 1.0 and t.params.get("y") == 3.0)
except StopIteration:
bayes_best_index = None
# ========= 結果表示 =========
df_results = pd.DataFrame([
{"Method": "Grid Search", "x": grid_best[0], "y": grid_best[1],
"f(x,y)": grid_best[2], "Step Found (x=1,y=3)": grid_best_index},
{"Method": "Random Search", "x": random_best[0], "y": random_best[1],
"f(x,y)": random_best[2], "Step Found (x=1,y=3)": random_best_index},
{"Method": "Bayesian Opt", "x": bayes_best[0], "y": bayes_best[1],
"f(x,y)": bayes_best[2], "Step Found (x=1,y=3)": bayes_best_index}
])
print("=== Booth関数 最適化結果 ===")
print(df_results)最適解$ (x, y) = (1, 3) $に辿り着くまでの試行回数は以下の通りでした。
- グリッドサーチ:504回目
あらかじめ用意された1000通りの組合せのうち、上から順に1000点を試行。最適解は504回目に出現し、そこで最小値に到達しています。
- ランダムサーチ:671回目
探索点1000通りの中からランダムに選んで評価。最適解 に671回目で辿り着いたものの、ランダムに選択しているため遅れる可能性もあり。
- ベイズ最適化:295回目
試行ごとに予測モデルを更新しながら有望な点を選んで探索。早い段階(295回目)で最適解に到達しており、効率の高さが際立っています。
Booth関数のような明確な最適点を持つケースでは、ベイズ最適化が高効率であることが示されました。
今回は数値最適化問題において各手法を比較しましたが、パラメータチューニングでも同様に機械学習モデルの性能が向上するような最適値を見つけることが重要になります。
また、グリッドサーチやランダムサーチは最適値までの試行回数が多くなっていましたが、チューニングするパラメータの数が少なかったり、一回の試行コストが低い場合はベイズ最適化よりも適している可能性があります。
そのため、用途や状況に合わせてチューニング手法を選択したり組み合わせることが重要と言えます。
学習ステップをさらに進めたい方へ
ハイパーパラメータを本質的に調整できるようになるためには、
「どの数値をどう変えるか」だけでなく、モデル内部で何が起きているのかを自分の言葉で説明できる状態になることが重要です。
次の学習ステップへ進むための土台づくりとしておすすめなのが、『図解即戦力 機械学習&ディープラーニングのしくみと技術がこれ一冊でしっかりわかる教科書』です。
本書は、数式やコードの細部に踏み込むのではなく、
アルゴリズムの考え方・構造・振る舞いを図解と文章で丁寧に整理することに特化した一冊です。
回帰・分類・クラスタリングといった代表的手法について、「なぜその挙動になるのか」「どのパラメータが何に効いているのか」を直感的に理解できます。
たとえば、SVM(RBFカーネル)における C や γ の役割、
Lasso・Ridge回帰における正則化の意味なども、
コードを書かなくても“調整の方向性を考えられるレベル”まで理解できる構成になっています。
そのため、
- 実装はできるが、ハイパーパラメータの意味を説明しきれない
- グリッドサーチやベイズ最適化を使っているが、探索範囲の設計に自信がない
- 次は数式やコードレベルの理解に進みたいが、その前に全体像を整理したい
といった方にとって、次の実践・実装フェーズへ進むためのインプットとして最適です。
本書で仕組みを整理したうえで、
コード実装やチューニング手法(グリッド/ランダム/ベイズ最適化)に取り組むことで、
「なぜその設定を試すのか」を考えながら学習を前に進められるようになります。
一方で「Pythonはこれから…」「数式で挫折したことがある…」という方もいらっしゃるかと思います。
そんな初学者の方でもpythonで機械学習を実装できるようになるためのロードマップとオススメの教材について以下の記事にまとめていますので、興味のある方はご覧になって下さい。
終わりに
いかがでしたでしょうか?以上がハイパーパラメータのチューニング手法に関する解説になります。ハイパーパラメータチューニングはモデル精度に直結する重要な工程です。ぜひ用途や状況に応じて最適な手法を選んでみてください!