【初心者向け】勾配ブースティング木（GBDT）とは？Python実装までやさしく解説

機械学習

こんにちは！ぼりたそです！

今回は勾配ブースティング木（GBDT）について特徴やアルゴリズム、Pythonでの実装までわかりやすく解説します。

この記事は以下のポイントでまとめています。

Point
  • GBDTとは？（決定木、ブースティング、勾配）
    　
  • GBDTの強み&弱み
    　
  • GBDTのアルゴリズム
    　
  • Pythonを使った実装

それでは順に解説していきます。

スポンサーリンク

1. GBDTとは？（決定木 × ブースティング × 勾配）

GBDT（Gradient Boosting Decision Tree）を一言で表すと、

「決定木を使って、予測の誤差を“勾配降下法”に基づいて少しずつ修正していくアルゴリズム」

です。

GBDTという名前は、次の3つの要素をそのまま組み合わせたものです。

  • Decision Tree（決定木）
  • Boosting（ブースティング）
  • Gradient（勾配）

つまりGBDTとは、

決定木を使い
弱いモデルを順番に足し算して
その修正方向を「勾配」によって決める

という学習アルゴリズムです。

この決定木、ブースティング、勾配について詳細に説明していきます。

決定木とは？

決定木は、

  • 「この特徴量が○以上なら△△」
  • 「それ以外なら××」

のように、条件分岐を繰り返して予測を行うモデルです。
人間の思考に近く、「なぜその予測になったのか」を説明しやすいという特徴があります。

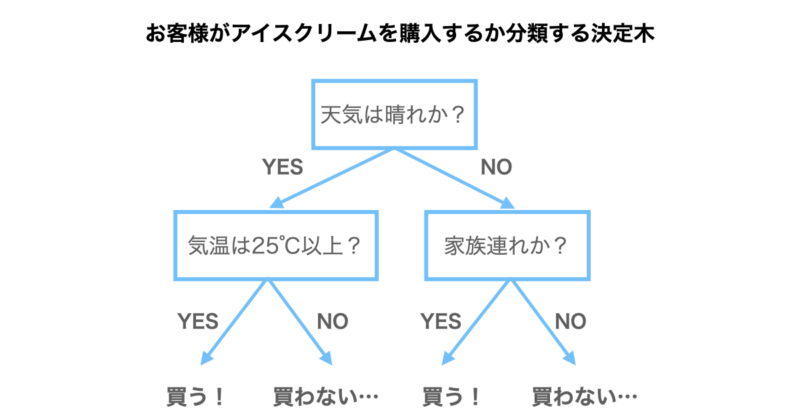
例としてお客さんがアイスクリームを購入するかしないかを予測したい場合をご紹介します。

下の図が決定木になっており、まず天気は晴れかという条件分岐があります。該当すればYES、該当しなければNOに進むことになります。

次に天気が晴れの場合は気温が25℃以上かという条件分岐に進み、ここで該当すれば恐らくアイスクリームを購入するだろうと予想されます。逆に該当しなければ購入しないだろうと予想されることになります。

一方で、決定木は1本だけだと、

  • 過学習しやすい
  • そもそも予測精度がそこまで高くない

といった弱点もあります。

そこで次に登場するのがブースティングという手法です。

ブースティングとは？

ブースティングとは、

「弱いモデルを何本も“順番に”足し算して、強いモデルにしていく考え方」

です。

GBDTでは、

  1. まずざっくりした予測をする
  2. その予測と正解のズレを見る
  3. そのズレだけを修正する新しい決定木を作る
  4. その修正分を元のモデルに足す

という流れを、何度も繰り返します。

つまりGBDTは、

「間違いを見つけて、その間違いだけを直す」ことをひたすら繰り返す学習法

だと考えると、かなり理解しやすいと思います。

では予測と正解のズレをどのように修正するかという疑問が浮かぶと思いますが、ここで登場するのが勾配降下法です。

勾配降下法とは？

GBDTの中で少し分かりにくいのが、この「勾配（gradient）」です。

GBDTでは単に

  • 「どれくらい間違ったか（誤差）」

を見るのではなく、

「どの方向に、どれくらいズレているか」

という情報まで含めた量を使います。
これが 勾配 です。

勾配とは、

  • 予測値を大きくすべきか、小さくすべきか
  • どれくらい修正すべきか

をまとめて教えてくれる 「誤差の向きと大きさ」 の情報だと考えてください。

GBDTでは、この 勾配だけを次の決定木に学習させて、予測を少しずつ修正していく勾配降下法 という手法を取り入れいています。

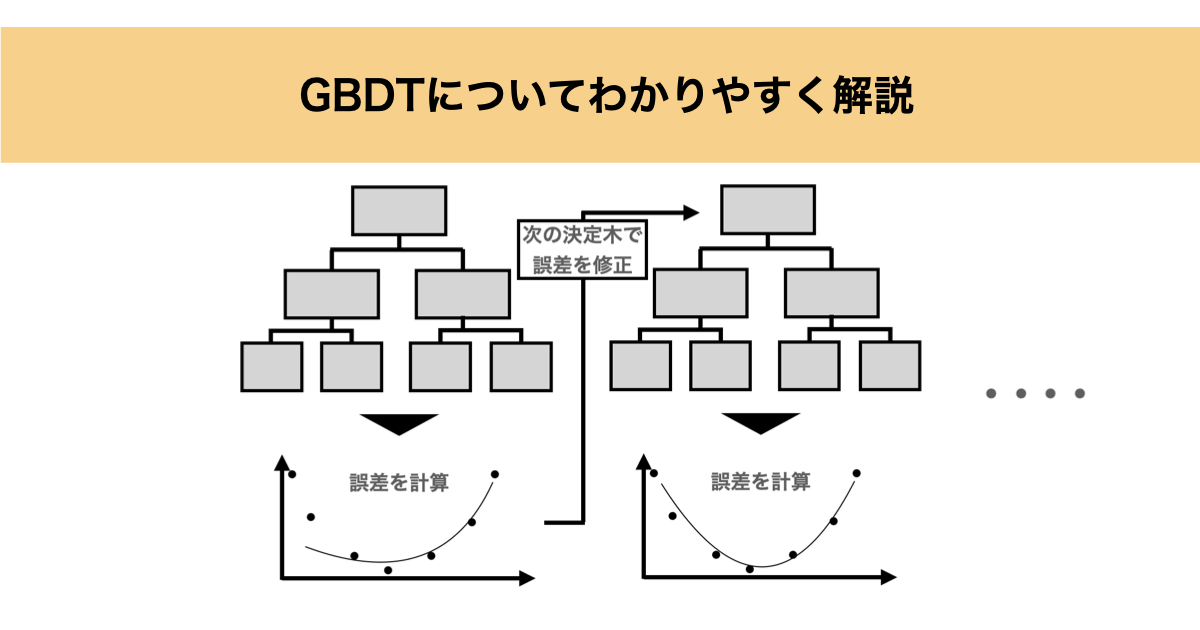
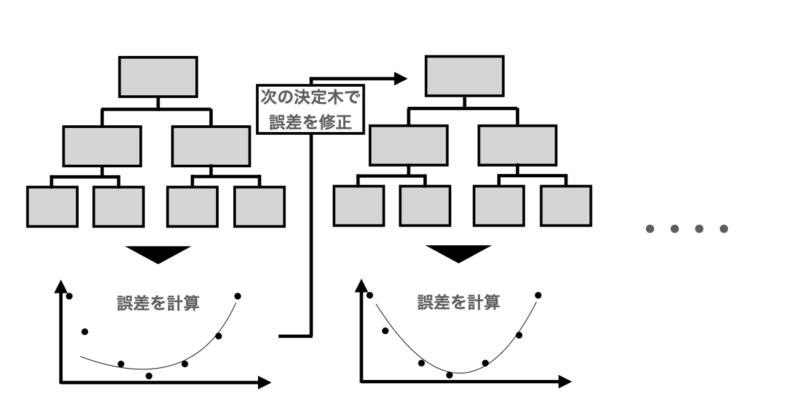
ここまでをまとめると、GBDTは

  1. 決定木で予測
  2. その予測のズレ（勾配）を計算
  3. ズレだけを予測する新しい木を作る
  4. その修正を元のモデルに足す

ということを、ひたすら繰り返すアルゴリズムです。以下に簡単なイメージ図を記載します。

GBDTの強み・弱み

ここからは、GBDTの強み・弱みについて特徴を整理します。

GBDTの強み

GBDTの最大の魅力は、とにかく精度が出やすいことです。それ以外にもたくさんの強みがあります。
以下にGBDTの主な強みと詳細について記載します。

● 少量データでも高精度が出やすい

深層学習と異なりパラメータ数が少なく、決定木の弱学習器を積み重ねる構造なので少量データでもそれなりの精度になります。

● 非線形な関係を自然に学習できる

決定木そのものが特徴量の条件分岐を組み合わせて表現力を持つため、線形モデルでは捉えきれない複雑な関係も扱えます。

● 特徴量の標準化が不要

決定木は絶対値そのものではなく「閾値での分割」によって学習するため、スケーリングの有無で性能が変わりません。
実務では前処理の手間が減り、データをそのままモデルに投入しやすいという大きなメリットになります。

● 欠損値処理が不要（実装による）

PythonライブラリであるXGBoost・LightGBM では欠損値処理で自動的に実行してくれるため、前処理負荷が軽くなります。

● 特徴量重要度が得られ、解釈しやすい

各決定木の分割にどの特徴量がどれだけ寄与したかを可視化できるため、予測モデルがブラックボックスになりにくいです。「この特徴が効いている」という定量的な理解が欲しい実務では大きな強みです。

GBDTの弱み

一方で、GBDTは万能ではありません。以下にその弱点を記載します。

● 外れ値やノイズの影響を受けやすい

勾配に基づいて誤差部分を重点的に学習するため、外れ値があるとそこに過剰に合わせてしまうことがあります。
また、決定木が「誤差部分に細かく適合する」特性上、ノイズにも適合しやすいという欠点があります。
木の深さ制限や データ分割 を活用することで過学習を防ぐことができます。

● 計算コストが大きく、大量データには不向きな場合がある

木を順番に学習していく“逐次型”モデルのため並列化しづらく、データ量が増えるほど重くなります。
PythonライブラリであるLightGBM のように高速化が得意な実装を使うことである程度解消可能です。

スポンサーリンク

GBDTのアルゴリズム

GBDTについては先述の通りとなりますが、具体的なアルゴリズムについて数式も交えつつ解説していきます。
ここでは、 損失関数 → 勾配 → 勾配降下法 → 決定木での実現 という流れで丁寧に解説します。

現在のデータで決定木予測

GBDT では、常に “今持っているモデル全体” を使って予測を行います。

y^(m−1)=Fm−1(x)\hat{y}^{(m-1)} = F_{m-1}(x)

y^(m−1)\hat{y}^{(m-1)}：m−1m-1 回目まで学習したモデルの予測値
Fm−1(x)F_{m-1}(x)：m−1m-1 個の木を足し合わせた予測モデル

このステップは単なる予測ではなく、

“ここからどれくらいズレているかを測るための基準点”

を作る工程です。

勾配も損失もこの値が基準になるため、
予測の更新は常に “積み重ね型” で行われます。

損失関数で予測誤差を数値化する

既存データで決定木の予測モデルを構築したら次に、

予測がどれくらい間違っているのか？を測る必要があります。

その役割を担うのが 損失関数（Loss function） です。

回帰で最もよく使われる損失が「二乗誤差」です。

L(y,y^)=(y−y^)2L(y, \hat{y}) = (y – \hat{y})^2

L(y,y^)L(y, \hat{y})：損失関数
y{y}：実測値
y^\hat{y}：予測値

これは、正解値と予測値の差を大きくするとペナルティが大きくなるように設計された関数で、GBDT の目的は

この損失をできるだけ小さくすることです。

勾配の計算

損失を小さくするためには、

  • 予測値が「どちら側に」
  • 「どれくらい」ずれているか

を知らなければいけません。これを正確に教えてくれるのが先ほども紹介した 勾配（gradient）の計算 です。

損失関数を予測値 F(x)F(x)で微分すると、

∂L(y,F(x))∂F(x)\frac{\partial L(y, F(x))}{\partial F(x)}

という計算になります。

例えば二乗誤差の場合は、

∂L(y,F(x))∂F(x)=−2(y−F(x))\frac{\partial L(y, F(x))}{\partial F(x)} = -2(y – F(x))

となり、これは予測が正解より小さければ負の値、大きければ負の正になるという性質を持ちます。

つまり、

  • 勾配が正 →「予測を小さくすべき」
  • 勾配が負 →「予測を大きくすべき」

という 損失を減らすための方向 を計算できるのです。

勾配情報から次の決定木を学習する

GBDTは各データ点に対して、勾配を誤差として新しい木の「教師データ」として利用します。

ri=−∂L(yi,Fm−1(xi))∂Fm−1(xi)r_i = -\frac{\partial L(y_i, F_{m-1}(x_i))}{\partial F_{m-1}(x_i)}

これは、勾配情報をそのまま使用しているので

  • 今のモデルが
  • 各データ点で
  • どの方向に、どれくらい間違っているか

を示す値です。

これを疑似残差と呼びます。

つまりGBDTは次の木に対して、

「正解値ではなく、誤差（＝勾配）を学習させる」ため

  • 各特徴量を使い
  • どの領域で誤差が大きいか
  • どういう方向に修正すべきか

を学習します。

これにより、次の木は “誤差の形”を表現するモデル になります。

モデルの更新

最後に「勾配を学んだ木」を少しだけ足すことでモデルを更新します。

更新式は次のとおりです。

Fm(x)=Fm−1(x)+ηhm(x)F_m(x) = F_{m-1}(x) + \eta h_m(x)

ここで、

  • Fm−1(x)F_{m-1}(x)：これまでの予測
  • hm(x)h_m(x)：誤差（勾配）を学習した木
  • η\eta：学習率（どれくらい慎重に進むか）

を表します。

全体の流れ

以上をまとめると、GBDT は次のステップを繰り返すアルゴリズムです。

  1. 現在のモデルで予測
  2. 損失を計算
  3. 損失の勾配（＝誤差の向き・大きさ）を求める
  4. その勾配だけを学習する新しい決定木を作る
  5. その木を少しだけ足してモデルを更新

ところが、たったこれだけの仕組みなのに、表形式データでは非常に強力な性能を発揮するのがGBDTの特徴です。

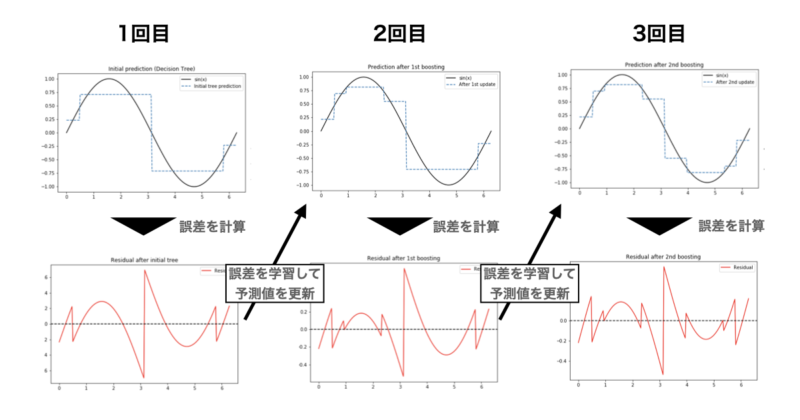
わかりやすいようにsin(x)に対して3回 GBDTによる学習を行った際の回帰線とその誤差を下に記載いたします。

1回目はsin(x)の曲線に対して全くフィットしていませんでしたが、誤差から学習して決定木をブースティングすることで2回、3回目と徐々にフィットしていることが確認できるかと思います。

Pythonで実装

では、実際にPythonにてGBDTを実装します。

本章では、GBDT（勾配ブースティング木）の代表的な実装である XGBoost を用いて、回帰問題を実際に解いていきます。

XGBoost（eXtreme Gradient Boosting）は、その名の通り 勾配ブースティングを高速かつ安定に実装したライブラリで、以下のような特徴があります。

  • GBDTをベースにした高精度な予測モデル
  • 正則化（L1 / L2）を標準でサポートし、過学習しにくい
  • early stopping により過学習を自動で防げる
  • 表形式データ（tabular data）に非常に強い

そして、今回扱う回帰問題は「カリフォルニア住宅価格予測」です。

目的変数：MedHouseVal（各地区における住宅価格の中央値）

説明変数：以下テーブルの通りです

変数名内容
MedInc地区の世帯収入の中央値
HouseAge住宅の平均築年数
AveRooms世帯あたりの平均部屋数
AveBedrms世帯あたりの平均寝室数
Population地区の人口
AveOccup世帯あたりの平均居住人数
Latitude緯度
Longitude経度

線形回帰では表現しづらい関係をGBDT（XGBoost）がどのように学習していくのかを確認する題材として、この住宅価格予想のデータセットを選択しています。

以上の条件で実行したPythonコードを以下に記載します。

import numpy as np
import matplotlib.pyplot as plt
import xgboost as xgb
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 1) データ
data = fetch_california_housing()
X = pd.DataFrame(
    data.data,
    columns=data.feature_names
)
y = data.target

X_train, X_tmp, y_train, y_tmp = train_test_split(X, y, test_size=0.3, random_state=0)
X_valid, X_test, y_valid, y_test = train_test_split(X_tmp, y_tmp, test_size=0.5, random_state=0)

# 2) DMatrix（xgboostの高速内部形式）
dtrain = xgb.DMatrix(X_train, label=y_train)
dvalid = xgb.DMatrix(X_valid, label=y_valid)
dtest  = xgb.DMatrix(X_test,  label=y_test)

# 3) パラメータ（回帰）
params = {
    "objective": "reg:squarederror",   # 回帰問題用の目的関数（二乗誤差を最小化）
    "eval_metric": "rmse",             # 学習・検証時に表示する評価指標（RMSE）
    "learning_rate": 0.03,             # 学習率：1本の木をどれだけ強く反映させるか
    "max_depth": 4,                    # 各決定木の最大深さ（大きいほど複雑・過学習しやすい）
    "subsample": 0.8,                  # 各木で使用するデータの割合（過学習抑制）
    "colsample_bytree": 0.8,           # 各木で使用する特徴量の割合（ランダム性付与）
    "lambda": 1.0,                     # L2正則化項（重みを小さく保つ）
    "alpha": 0.0,                      # L1正則化項（不要な分割を抑制）
    "seed": 0,                         # 乱数シード（結果の再現性確保）
}


# 4) 学習（途中経過ログ + early stopping）
evals_result = {}                      # 各 boosting round の評価指標（RMSE）を保存する辞書

bst = xgb.train(
    params=params,                     # 上で定義したハイパーパラメータ
    dtrain=dtrain,                     # 学習用データ（DMatrix）
    num_boost_round=5000,              # 最大の boosting round（木の本数）
    evals=[                            # 学習中に評価するデータセット
        (dtrain, "train"),             # train：学習データでの評価（参考用）
        (dvalid, "valid")              # valid：検証データでの評価（過学習チェック用）
    ],
    early_stopping_rounds=200,          # valid の性能が200 round改善しなければ学習停止
    evals_result=evals_result,          # 各 round の評価結果を辞書に保存
    verbose_eval=100,                   # 100 round ごとに評価指標（RMSE）を表示
)

print("Best iteration:", bst.best_iteration)  # 検証データで最良だった boosting round
print("Best valid RMSE:", bst.best_score)     # そのときの検証 RMSE

# 5) テスト評価

# 学習済みモデルでテストデータを予測
y_pred = bst.predict(dtest)

# テストデータに対する RMSE を計算
rmse_test = np.sqrt(mean_squared_error(y_test, y_pred))
print("Test RMSE:", rmse_test)

# 6) 学習曲線
train_rmse = evals_result["train"]["rmse"]
valid_rmse = evals_result["valid"]["rmse"]

plt.figure()
plt.plot(train_rmse, label="train RMSE")
plt.plot(valid_rmse, label="valid RMSE")
plt.xlabel("boosting round")
plt.ylabel("RMSE")
plt.legend()
plt.show()

# 7) 変数重要度

# 学習済みモデルにおける特徴量重要度を表示
# デフォルトでは gain（損失削減への寄与度）で評価される
plt.figure()
xgb.plot_importance(bst, max_num_features=10)
plt.show()

コードの出力結果について順に説明していきます。

学習ログ（verbose 出力）

学習中、以下のようなログが一定間隔（100 round ごと）で表示されたはずです。

[0]	train-rmse:1.13328	valid-rmse:1.13334
[100]	train-rmse:0.56754	valid-rmse:0.59832
[200]	train-rmse:0.49808	valid-rmse:0.53728
...

ここで表示されているのは、

  • train-rmse
    → 学習データに対する誤差
  • valid-rmse
    → 検証データに対する誤差

となります。

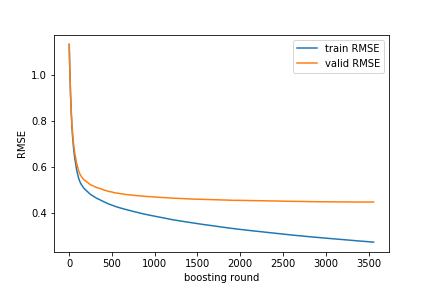
注目ポイントとして、train-rmse は学習が進むにつれて ほぼ単調に減少します。これは、 GBDTのアルゴリズムとして誤差を小さくするようにブースティングして学習するからです。

一方、valid-rmse は最初はtrain-rmseと同様に減少しますが、途中で最小値を取りそれ以降は横ばいになるという挙動を示すことが一般的です。これは、モデルが「学習データにはよく適合しているが、汎化性能は頭打ちになった」状態を意味します。

実際に今回の学習曲線は以下のように出力されています。

最終的なモデル汎化性能

学習完了後、test データに対して次の値が出力されました。

Test RMSE: 0.44387695736687716

ここでの test RMSE は、学習にも検証（early stopping）にも一切使われていない 完全な未知データ に対する誤差です。

つまりこの値が、今回構築した GBDT モデルの「本当の汎化性能」を表しています。

valid RMSE と test RMSE が大きく乖離していなければ、過学習は抑えられており、モデルは安定していると判断できます。

5. 特徴量重要度の解釈

最後に表示した特徴量重要度のグラフは、

「どの特徴量が住宅価格予測に強く寄与したか」

を示しています。

XGBoost のデフォルト設定では、gain（損失削減への寄与度）に基づいて重要度が算出されます。

今回の実行コードでは以下のように出力されています。

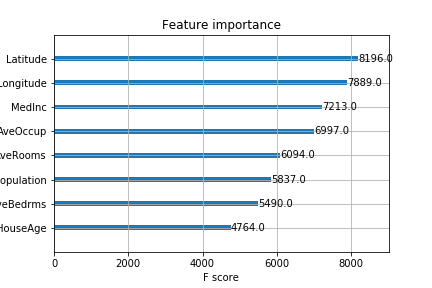
この出力結果から、Latitude / Longitude およびMedInc（世帯収入中央値） が上位であり、住宅価格に大きく寄与すると解釈することができます。

このように、GBDT は高い予測精度と解釈性を両立できる点も大きな魅力です。

まとめ

以上が GBDTの解説になります。一見難しそうなアルゴリズムですが、一つ一つ紐解いていくと理解しやすいのではなかったでしょうか？Kaggleなどの機械学習コンペで上位ランカーが使用しているモデルには GBDTがよく使用されており、積極的に使いこなしていきたいですね。

スポンサーリンク
タイトルとURLをコピーしました