こんにちは!ぼりたそです!
今回はPythonで重回帰分析を実装してみました。
重回帰分析については以下の記事を参考にしてくださればと思います。
この記事は以下のポイントでまとめています。
- データセット生成
- 多重共線性について確認
- 重回帰分析の実行
- 標準化回帰係数
それでは詳細に説明いたします。
データセットの生成
まず、データセットの生成を実行します。
今回は成人男性の1日の摂取カロリー[kcal]と1日の運動時間[hr]に対する体重[kg]として
■説明変数 1日の摂取カロリー[kcal]、1日の運動時間[hr]
■目的変数 体重[kg]
のデータセットを生成します。
データセットは以下の条件をもとにPythonで生成しました。
- 摂取カロリーの範囲は1000から10000 (int型)
- 運動時間の範囲は0〜12 (float型)
- 体重の範囲は40〜150 (float型)
- 摂取カロリーと運動時間は多重共線性を回避する
- データの分布がある程度正規性を持つようにする
import numpy as np
import pandas as pd
np.random.seed(42)
# データ数
data_size = 1000
# 摂取カロリーの範囲とデータ生成
calories = np.random.randint(1000, 6000, data_size)
# 運動時間の範囲とデータ生成
exercise_hours = np.random.randint(0, 24, data_size)
# 摂取カロリーと体重のデータを正規分布に従わせる
calories = np.random.normal(loc=calories.mean(), scale=700, size=data_size).round().astype(int)
exercise_hours = np.random.normal(loc=exercise_hours.mean(), scale=7, size=data_size).round(2)
# 体重の範囲とデータ生成(摂取カロリーと運動時間に対して相関を持たせる)
weights = 0.02 * calories + -1.3 * exercise_hours + np.random.normal(loc=0, scale=10, size=data_size)
# 体重が40以下、カロリーが1000以下、運動時間が0以下、24以上の行を削除
data = pd.DataFrame({'Calories': calories, 'ExerciseHours': exercise_hours, 'Weight': weights})
data = data[data['Weight'] > 40]
data = data[data['Calories'] > 1000]
data = data = data[data['ExerciseHours'] < 24]
data = data[data['ExerciseHours'] > 0]
# データの分布を確認
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.hist(data['Calories'], bins=20, edgecolor='k')
plt.xlabel('Calories')
plt.ylabel('Frequency')
plt.subplot(1, 3, 2)
plt.hist(data['ExerciseHours'], bins=13, edgecolor='k')
plt.xlabel('Exercise Hours')
plt.subplot(1, 3, 3)
plt.hist(data['Weight'], bins=20, edgecolor='k')
plt.xlabel('Weight')
plt.tight_layout()
plt.show()
データ分布は以下のようになっています。
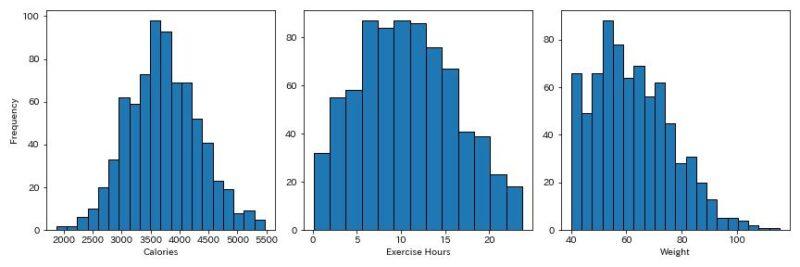

左から摂取カロリー、運動時間、体重のヒストグラムになっていますが、ある程度正規分布に則っていますね。(体重とかは怪しいですが…)
多重共線性の確認
次に生成したデータに多重共線性がないか確認します。
今回、多重共線性の指標としてVIF(Variance Inflation Factor)を使用します。
VIFが高いということは、説明変数間に強い相関がある可能性が高いことを示し、5<VIFであると多重共線性があると言われています。
以下にVIFを計算するPythonのコードを示します。
import numpy as np
import pandas as pd
np.random.seed(42)
# データ数
data_size = 1000
# 摂取カロリーの範囲とデータ生成
calories = np.random.randint(1000, 6000, data_size)
# 運動時間の範囲とデータ生成
exercise_hours = np.random.randint(0, 24, data_size)
# 摂取カロリーと体重のデータを正規分布に従わせる
calories = np.random.normal(loc=calories.mean(), scale=700, size=data_size).round().astype(int)
exercise_hours = np.random.normal(loc=exercise_hours.mean(), scale=7, size=data_size).round(2)
# 体重の範囲とデータ生成(摂取カロリーと運動時間に対して相関を持たせる)
weights = 0.02 * calories + -1.3 * exercise_hours + np.random.normal(loc=0, scale=10, size=data_size)
# 体重が40以下、カロリーが1000以下、運動時間が0以下、24以上の行を削除
data = pd.DataFrame({'Calories': calories, 'ExerciseHours': exercise_hours, 'Weight': weights})
data = data[data['Weight'] > 40]
data = data[data['Calories'] > 1000]
data = data = data[data['ExerciseHours'] < 24]
data = data[data['ExerciseHours'] > 0]
# 説明変数をXに設定
X = data[['Calories', 'ExerciseHours']]
# 各説明変数のVIFを計算
vif = pd.DataFrame()
vif['Features'] = X.columns
vif['VIF'] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
# 結果の出力
print(vif)
#結果出力
# Features VIF
#0 Calories 4.945457
#1 ExerciseHours 4.945457VIFが4.95とギリギリ多重共線性がないくらいですね。(小生がそのくらいに調整したのですが…)
重回帰分析の実装
次にいよいよ重回帰分析の実装をしていきます。
今回は単純にscikit-learnにて重回帰分析を実行していてPythonのコードは以下のようになっています。
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(42)
# データ数
data_size = 1000
# 摂取カロリーの範囲とデータ生成
calories = np.random.randint(1000, 6000, data_size)
# 運動時間の範囲とデータ生成
exercise_hours = np.random.randint(0, 24, data_size)
# 摂取カロリーと体重のデータを正規分布に従わせる
calories = np.random.normal(loc=calories.mean(), scale=700, size=data_size).round().astype(int)
exercise_hours = np.random.normal(loc=exercise_hours.mean(), scale=7, size=data_size).round(2)
# 体重の範囲とデータ生成(摂取カロリーと運動時間に対して相関を持たせる)
weights = 0.02 * calories + -1.3 * exercise_hours + np.random.normal(loc=0, scale=10, size=data_size)
# 体重が40以下、カロリーが1000以下、運動時間が0以下、24以上の行を削除
data = pd.DataFrame({'Calories': calories, 'ExerciseHours': exercise_hours, 'Weight': weights})
data = data[data['Weight'] > 40]
data = data[data['Calories'] > 1000]
data = data[data['ExerciseHours'] < 24]
data = data[data['ExerciseHours'] > 0]
# 重回帰分析を実行
X = data[['Calories', 'ExerciseHours']]
X = sm.add_constant(X)
y = data['Weight']
model = sm.OLS(y, X).fit()
# 回帰係数を表示
print("回帰係数:")
print(model.params)
# R^2値を表示
print("R^2値:", model.rsquared)
# 回帰後のプロットと予測平面を図示
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data['Calories'], data['ExerciseHours'], data['Weight'], c='b', marker='o', label='Data')
# プロット範囲を指定
calories_range = np.linspace(data['Calories'].min(), data['Calories'].max(), 50)
exercise_hours_range = np.linspace(data['ExerciseHours'].min(), data['ExerciseHours'].max(), 50)
calories_range, exercise_hours_range = np.meshgrid(calories_range, exercise_hours_range)
weights_predicted = model.params[0] + model.params[1] * calories_range + model.params[2] * exercise_hours_range
# 予測平面を図示
ax.plot_surface(calories_range, exercise_hours_range, weights_predicted, color='r', alpha=0.5, label='Prediction Plane')
ax.set_xlabel('Calories')
ax.set_ylabel('Exercise Hours')
ax.set_zlabel('Weight')
plt.show()
#結果出力
#回帰係数:
#const 10.669962
#Calories 0.016928
#ExerciseHours -1.052963
#dtype: float64
#R^2値: 0.5774989226259657回帰係数は摂取カロリーが0.016, 運動時間が-1.05となっています。実はコードの中で回帰係数がだいたいこのくらいになるように調整してあるので、こんなもんかなといった感じですね。
$R^2$値に関しては0.58とそれなりに合っているかなという印象です。適当に生成したデータセットにしては妥当な数値ですね。
予測結果を3Dグラフで表示すると下のようになります。
予測平面も赤色で示してありますが、$R^2$値が0.58なので少しバラツキがありますね。
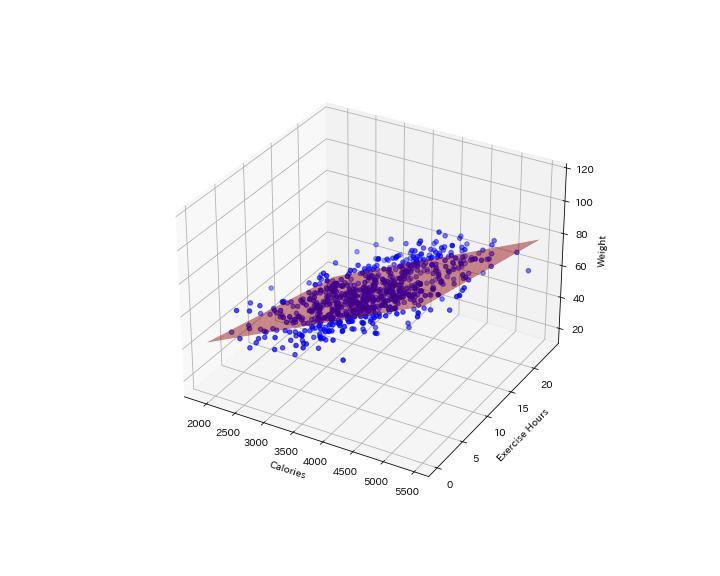

標準化回帰係数
最後に変数の重要度を比較するために標準化回帰係数を計算したいと思います。
標準化回帰係数はデータを全て標準化した上で求める回帰係数なので、先ほどのデータを単純に標準化すれば算出できます。
Pythonコードは以下のものを使用しています。
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.preprocessing import StandardScaler
np.random.seed(42)
# データ数
data_size = 1000
# 摂取カロリーの範囲とデータ生成
calories = np.random.randint(1000, 6000, data_size)
# 運動時間の範囲とデータ生成
exercise_hours = np.random.randint(0, 24, data_size)
# 摂取カロリーと体重のデータを正規分布に従わせる
calories = np.random.normal(loc=calories.mean(), scale=700, size=data_size).round().astype(int)
exercise_hours = np.random.normal(loc=exercise_hours.mean(), scale=7, size=data_size).round(2)
# 体重の範囲とデータ生成(摂取カロリーと運動時間に対して相関を持たせる)
weights = 0.02 * calories + -1.3 * exercise_hours + np.random.normal(loc=0, scale=10, size=data_size)
# 体重が40以下、カロリーが1000以下、運動時間が0以下、24以上の行を削除
data = pd.DataFrame({'Calories': calories, 'ExerciseHours': exercise_hours, 'Weight': weights})
data = data[data['Weight'] > 40]
data = data[data['Calories'] > 1000]
data = data[data['ExerciseHours'] < 24]
data = data[data['ExerciseHours'] > 0]
# データの標準化
scaler = StandardScaler()
X = data[['Calories', 'ExerciseHours']]
X_scaled = scaler.fit_transform(X)
y = data['Weight'].values.reshape(-1, 1)
y_scaled = scaler.fit_transform(y)
# 重回帰分析を実行
X_scaled = sm.add_constant(X_scaled)
model = sm.OLS(y_scaled, X_scaled).fit()
# 標準化回帰係数を表示
print("標準化回帰係数:")
coef_names = ['Intercept', 'Calories', 'ExerciseHours']
coef_values = model.params
for name, value in zip(coef_names, coef_values):
print(f"{name}: {value}")
# R^2値を表示
print("R^2値:", model.rsquared)
#出力結果
#標準化回帰係数:
#Intercept: -1.734723475976807e-16
#Calories: 0.7318112450909993
#ExerciseHours: -0.41031861986954987
#R^2値: 0.5774989226259659
標準化回帰係数について摂取カロリーが0.73, 運動時間が-0.41なので絶対値で見ると摂取カロリーの方がやや重要なパラメータとなってくるようですね。
Interceptは切片であり、標準化すると0になるのですが計算上わずかにずれるようです。(ほぼ0ですけどね)
終わりに
以上がPythonを使った重回帰分析の実装になります。重回帰分析は比較的簡単に実装できますが、多重共線性に注意したりしないと正しい結果が得られないことがあるので注意です。



