こんにちは！ぼりたそです！
今回は最尤推定法についてわかりやすく解説していきます。最尤推定法は統計モデルのパラメータを推定するために使用されたりします。
この記事は以下のポイントでまとめています。
- 最尤推定法とは？
- 尤度関数とは？
- 二項分布の最尤推定
- 正規分布の最尤推定
それでは詳細に解説していきます。
最尤推定法とは？
まずは最尤推定法について解説していきます。
最尤推定法は、統計モデルのパラメータを推定するための手法です。観測されたデータが与えられた際に、そのデータが最も起こりやすい（最も尤もらしい）パラメータの値を見つけることを目指します。
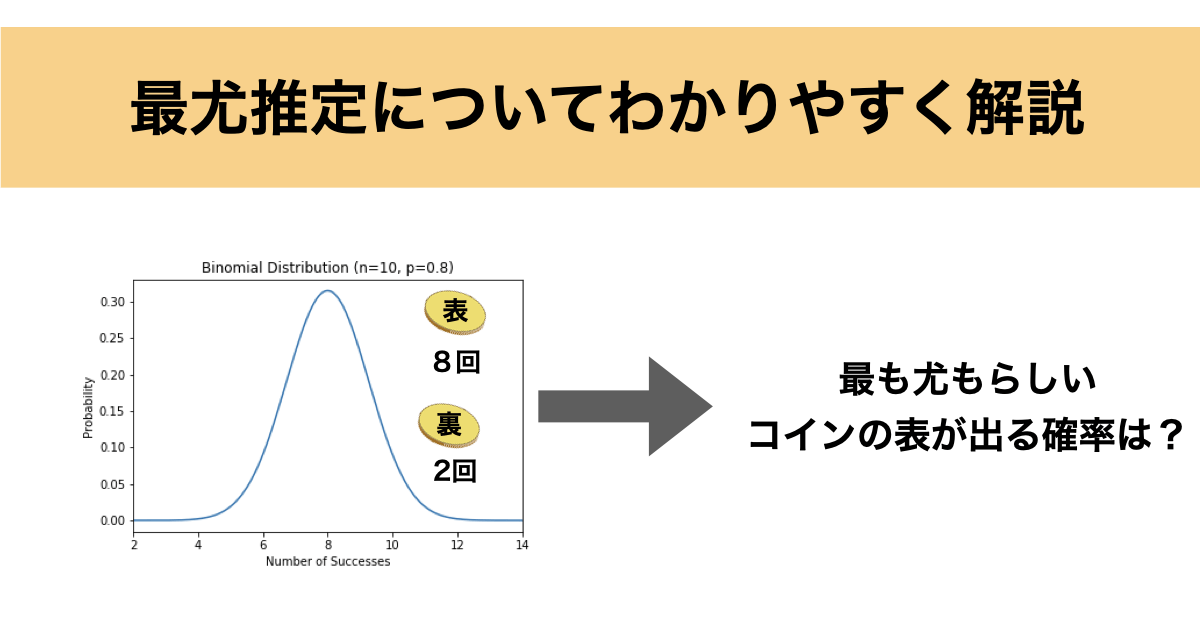
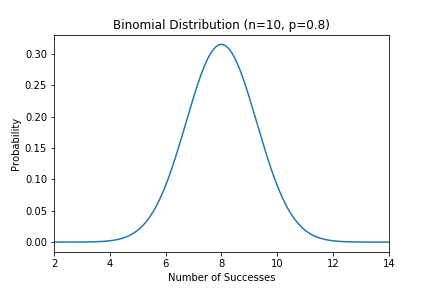
例えば、コインを10回投げて8回表が出たとします。
この場合のコインの表が出る確率として最も尤もらしいのは直感的に0.8 (80%)となると思います。
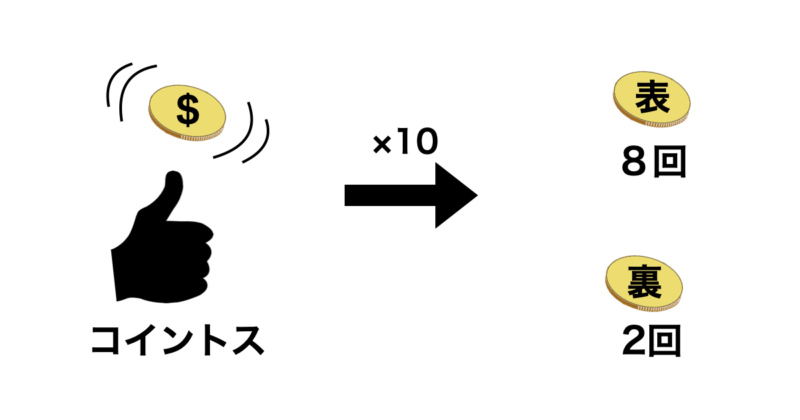
実際に最尤推定法で算出すると0.8になります。
ここからは実際に数式を例にして解説していきます。
尤度関数について
先ほどのコインの表が出る確率については、統計学でよく知られる二項分布で表すことができます。
コインの表が出る確率を$\theta$、試行回数を$n$、表が出た回数を$k$としたとき$L(\theta) $として以下のように表せます。
$$L(\theta) = {}_n C_k \cdot \theta^k \cdot (1 – \theta)^{n – k}$$
誰もが知っている二項分布の形ですね。
また、この$L(\theta) $を尤度関数と言います。
尤度関数は、統計モデルにおいて、あるパラメータが与えられた条件下で観測されたデータがどの程度起こりやすいかを表す関数です。つまり、観測されたデータがあるパラメータや複数のパラメータに従う確率分布から生成されたときに得られる尤もらしさ（尤度）を示します。
少し分かりにくいと思いますので、実際に例を交えます。
先ほどの様にコインを10回投げて8回表が出たとします。
このとき、表が出る確率$L(\theta) $について
$\theta = 0.1$の場合
$L(\theta) = {}_1{}_0 C_8 \cdot 0.1^8 \cdot (1 – 0.1)^{10 – 8}$
$L(\theta) = 3.6 \times 10^{-7}$
$\theta = 0.8$の場合
$L(\theta) = {}_1{}_0 C_8 \cdot 0.8^8 \cdot (1 – 0.8)^{10 – 8}$
$L(\theta) = 0.30$
それぞれの尤度に注目すると$\theta = 0.8$の方が圧倒的に尤度が大きいですね。
なのでこの場合は0.8の方が尤もらしいということになります。
二項分布の最尤推定
では次に実際に二項分布の最尤推定を行なっていきます。
先述の通り、最も尤もらしくなるような$\theta$を見つけるのが最尤推定となります。
ではどうやって求めるのかというと、 $L(\theta)$ の微分が0になる点（ $L(\theta)$ の極大点）を計算してやればいいのです。
ただ、 $L(\theta)$ をそのまま微分すると計算が面倒なので、log（自然対数）で括ってから微分してみましょう。
ちなみに対数をとった尤度関数は対数尤度関数と呼ばれます
$L(\theta) = {}_n C_k \cdot \theta^k \cdot (1 – \theta)^{n – k}$
$\log L(\theta) = \log({}_n C_k \cdot \theta^k \cdot (1 – \theta)^{n – k})$
積の対数は対数の和に変換できるので、以下の式に変形します。
$\log L(\theta) = \log ({}_n C_k) + k \log(\theta) + (n – k) \log(1 – \theta)$
$\frac{d}{d\theta}(\log L(\theta)) = \frac{k}{\theta} – \frac{n – k}{1 – \theta}$
微分した値が0になればいいので、
$\frac{k}{\theta} – \frac{n – k}{1 – \theta} = 0$
$\theta = \frac{k}{n}$
最終的には $\theta = \frac{k}{n}$ となりましたね。最初出した例だとコインを10回投げて表が8回出ているので、 $\theta = 0.8 $ が最尤であることがわかりますね。
正規分布の最尤推定
最尤推定について、何となく理解していただけたと思うのですが、最後にパラメータが二つある例として正規分布の最尤推定について解説していきます。
正規分布の平均と分散の最尤推定を行う場合、観測されたデータが $x_1, x_2, \ldots, x_n$ とします。これらのデータは独立同分布で、平均を $\mu$、分散を $\sigma^2$ とする正規分布 $N(\mu, \sigma^2)$ から生成されたものと仮定します。
この仮定のもとで、正規分布の尤度関数を考えます。正規分布の尤度関数は以下のようになります。
$x_1, x_2, \ldots, x_n$が与えられた時、全ての$x$が同じ分布となるので、尤度関数はそれぞれのデータ$x$の積で表すことができます。
また、正規分布では平均 $\mu$、分散 $\sigma^2$ とパラメータが二つ存在します。
$$L(\mu, \sigma^2) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x_i – \mu)^2}{2\sigma^2}\right)$$
では、この尤度関数を用いて最尤推定を行なっていきますが、今回はパラメータが二つあるので、それぞれのパラメータで偏微分していきます。
まず、二項分布の時と同様に対数尤度関数に変形していきます。
$$\log L(\mu, \sigma^2) = \sum_{i=1}^{n} \left(-\frac{1}{2}\log\frac{1}{\sqrt{2\pi}\sigma} – \frac{1}{2}\left(\frac{x_i – \mu}{\sigma}\right)^2\right)$$
■平均 $\mu$ の最尤推定
ではまず、平均 $\mu$ の最尤推定から行います。
対数尤度関数について $\mu$ の偏微分を行います。
$\frac{d}{d\mu}(\log L(\mu, \sigma^2)) = \sum_{i=1}^{n} \frac{x_i – \mu}{\sigma^2}$
偏微分が0になればいいので、
$ \sum_{i=1}^{n} \frac{x_i – \mu}{\sigma^2} = 0$
$\frac{1}{\sigma^2} \sum_{i=1}^{n}(x_i – \mu) = 0$
$n\mu = \sum_{i=1}^{n} x_i$
$\mu = \frac{1}{n} \sum_{i=1}^{n} x_i $
皆さんが知っている $\mu = \frac{1}{n} \sum_{i=1}^{n} x_i $ の形になりましたね。
■分散 $\sigma^2$ の最尤推定
次に $\sigma^2$ の最尤推定ですが、こちらも同様に対数尤度関数について $\sigma^2$ の偏微分を行います。
$\frac{d}{d(\sigma^2)}(\log L(\mu, \sigma^2)) = \sum_{i=1}^{n} \left(-\frac{1}{2\sigma^2} + \frac{(x_i – \mu)^2}{2\sigma^4}\right) $
偏微分が0になればいいので、
$ \sum_{i=1}^{n} \left(-\frac{1}{2\sigma^2} + \frac{(x_i – \mu)^2}{2\sigma^4}\right) = 0$
$\frac{1}{2\sigma^4} \sum_{i=1}^{n} (x_i – \mu)^2 = \frac{1}{2\sigma^2}n$
$\frac{1}{\sigma^2} \sum_{i=1}^{n} (x_i – \mu)^2 = n$
$\sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i – \mu)^2$
分散 $\sigma^2$ も皆さんがご存じの $\sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i – \mu)^2$ の形に変形されましたね。
以上が正規分布の平均 $\mu$、分散 $\sigma^2$ に関する最尤推定となります。
終わりに
いかがでしたでしょうか？最尤推定について、某もそうでしたが初めて聞く方には少し難しいかなと思いますが、少しでも理解できるきっかけになれば幸いです。最尤推定はハイパーパラメータの計算などによく使用されますので、事細かな数式まで覚える必要はありませんが、どの様なことをしているかは理解できると良いと思います！
