こんにちは!ぼりたそです!
今回は決定木についてわかりやすく説明した記事を作成しました。実際にPythonを用いて決定木による分類を実行してみたのでご参考いただければと思います。
この記事は以下のポイントでまとめています。
- 決定木とは?
- 決定木のメリット、デメリット
- 決定木の実行プロセス
- Pythonによる実行
それでは詳細に解説していきます!
決定木とは?
まず決定木について概要を説明します。
決定木とは条件分岐により意思決定を行う手法になります。
手法としてはクラス分類と回帰分析のどちらも実行することができます。
ここではクラス分類の例を用いてわかりやすく説明します。
例としてお客さんがアイスクリームを購入するかしないかを予測したい場合をご紹介します。
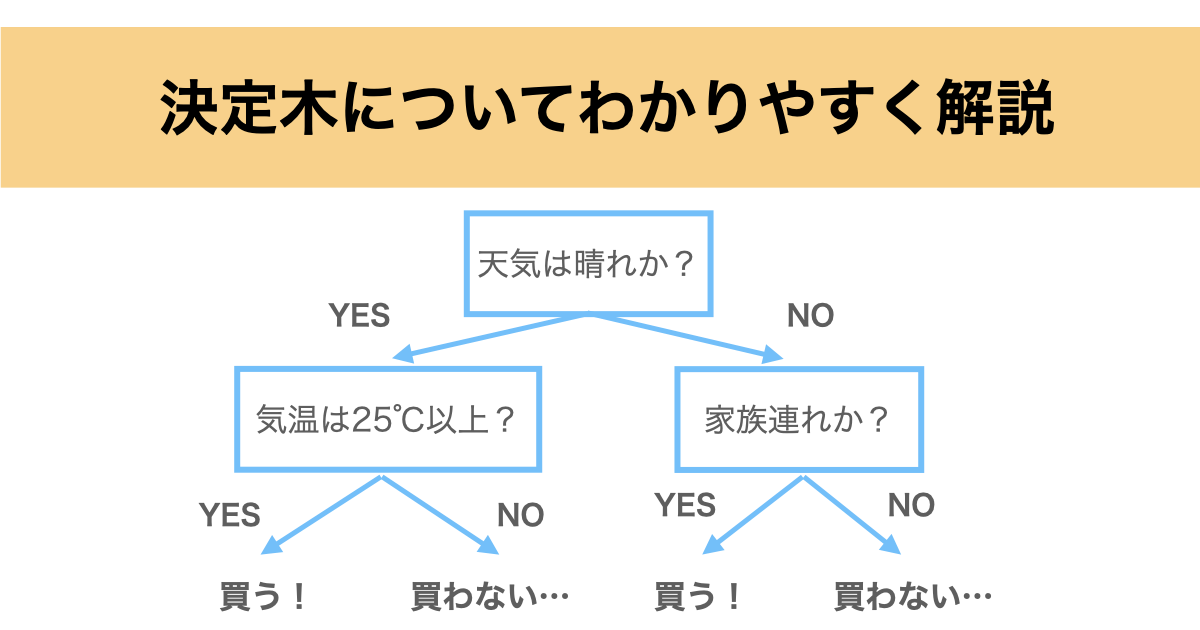
下の図が決定木になっており、まず天気は晴れかという条件分岐があります。該当すればYES、該当しなければNOに進むことになります。
次に天気が晴れの場合は気温が25℃以上かという条件分岐に進み、ここで該当すれば恐らくアイスクリームを購入するだろうと予想されます。逆に該当しなければ購入しないだろうと予想されることになります。
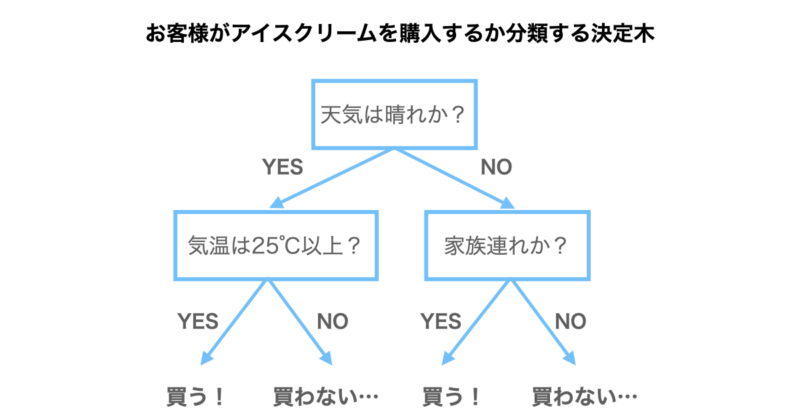
このように複数の条件分岐をもってクラス分類や回帰を行うことができるわけですね。
また、決定木の構造について少し説明します。
決定木の構造は大きく以下の4つとなります。
- ノード
条件分岐させるサンプル群のこと
- 根ノード
ノードの中でも決定木の頂点にあるノード
- 葉ノード
ノードの中でも決定木の末端にあるノード
- エッジ
ノードとノードを結ぶ線
先ほどの決定木の中でそれぞれの構造を記載しましたので、参考にしていただければと思います。
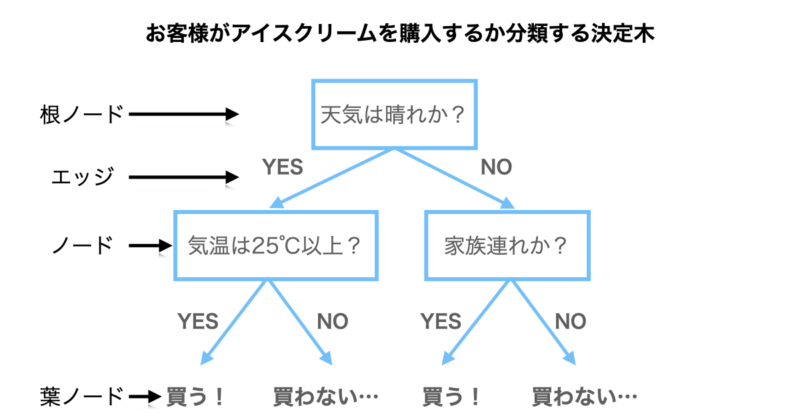
決定木のメリット、デメリット
次は決定木のメリット、デメリットについて説明します。
以下が具体的なメリット、デメリットになります。
■メリット
- 可視化:
決定木は木構造で表現されるため、非常に直感的で理解しやすいです。なので、条件分岐によってデータの分割や予測結果を解釈しやすいという特徴があります。
- 変数の重要度:
各変数の重要度を評価することができます。後にご説明しますが、ジニ不純度などにより、どの変数が重要か評価することができます。
- データの前処理が少ない:
決定木は特徴のスケーリングや正規化が必要ない場合が多く、欠損値の処理も行わずに使うことができます。
次にデメリットについて以下に示します。
■デメリット
- 過学習:
決定木は深くなると過学習しやすい傾向があります。適切な深さや枝刈りが重要です。
- データの偏りへの敏感さ:
クラスが不均衡な場合や外れ値が多い場合、決定木は適切に対処しづらいことがあります。
- モデルの安定性:
データの少しの変化に対して木の構造が大きく変わりやすいため、モデルの安定性が低い場合があります。
メリット、デメリットなど決定木の特徴を踏まえた上でモデルに使用するのが大事ですね。
決定木の実行プロセス
次に決定木による分類、または回帰を行う際のプロセスについて説明していきます。
決定木は大きく以下のプロセスで実行していきます。
- 木の深さ(ハイパーパラメータ)の設定
- 条件分岐の設定
- ジニ不純度および情報利得の計算
- 2-3を木の深さになるまで繰り返す
今回は先ほどの「アイスクリームの購入」に関する分類例を使用して順に説明していきます。
木の深さ(ハイパーパラメータ)の設定
まずは木の深さの設定について説明していきます。
決定木は木の深さというものがあり、決定木の垂直方向に何度条件分岐した数が木の深さに該当します。
今回、冒頭でご説明した決定木は2回条件分岐しているので、木の深さは2ということになります。
この木の深さはハイパーパラメータといい、決定木による分類または回帰を行う際にあらかじめ設定しておかなければならないパラメータとなります。
木の深さは深いほど学習データの分類精度は上がりますが、過学習状態となり他のデータを予測する汎化性能が低下することになります。
なので、きちんと分類しつつ、過学習にならないような木の深さを設定する必要があるということですね。
しかし、基本的には木の深さは自分で設定するというよりかはクロスバリデーションなどで最適な深さを自動で割り当てることがほとんどです。
条件分岐の設定
次に条件分岐の設定についてです。
条件分岐についてはどの説明変数を用いて、その閾値を設定することになります。
例で説明したアイスクリームの購入の決定木では最初に「天気は晴れか?」という条件分岐に設定しています。
つまり、説明変数は天気とし、閾値は晴れかどうかというところで条件分岐させていることになります。
しかし、どの説明変数を選択してどのような閾値にするのがいいのかなんてわかりませんよね。
それは次の情報利得とジニ不純度により決まります。
情報利得とジニ不純度の計算
では次に情報利得とジニ不純度の計算について説明します。
決定木において条件分岐が適切かどうかは情報利得によって評価します。
情報利得とは下に示すように条件分岐前(親ノード)のジニ不純度と条件分岐後(子ノード)のジニ不純度の差によって求められます。この情報利得が正の数であればきちんと分類できていることになります。
情報利得 = 親ノードのジニ不純度 ー $\left(\dfrac{子ノードのサンプル数}{親ノードのサンプル数}\right)$×子ノードのジニ不純度
ジニ不純度とはその名の通りどれだけデータの純度が高いか、言い換えればどれだけ分類できているかを表しており、データの純度が高いほどジニ不純度は小さくなります。
なので、条件分岐によりきちんと分類できていれば子ノードの方が不純度が小さくなり、情報利得は正の数をとることになります。
また、ジニ不純度については以下の一般式により計算することができます。
$$\text{Gini}(t) = 1 – \displaystyle\sum_{i=1}^{c} p(i|t)^2$$
$t$ = 対象のノード
$c$ = クラスの数
$i$ = クラス
$p(i|t)$ = ノード$t$におけるクラス$i$のサンプル割合
下に例としてアイスクリームの購入についての決定木を示しております。
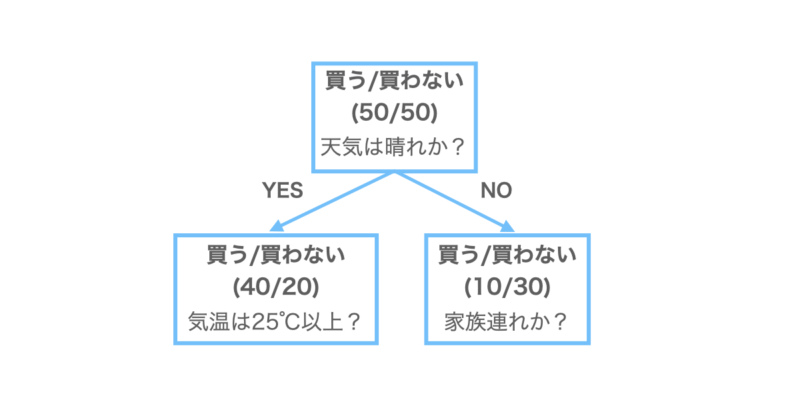
親ノードは買う人/買わない人が50/50の割合になっています。これを天気が晴れかどうかで分割することで、子ノードは買う/買わないの割合が40/20, 10/30になっています。それぞれジニ不純度を計算すると、
親ノードのジニ不純度 = $1-\left(\dfrac{50}{100}\right)^2+\left(\dfrac{50}{100}\right)^2$
= $0.5$
左の子ノードのジニ不純度 = $1-\left(\dfrac{40}{60}\right)^2+\left(\dfrac{20}{60}\right)^2$
= $0.44$
右の子ノードのジニ不純度 = $1-\left(\dfrac{10}{40}\right)^2+\left(\dfrac{30}{40}\right)^2$
= $0.375$
となります。
よって、情報利得は、
情報利得 = $0.5 – \left(\dfrac{60}{100}\right)\times 0.44 – \left(\dfrac{60}{100}\right)\times 0.375$
= $0.086$
となります。情報利得が正の数をとっているのでこの分割は意味のある分割ということができるのです。
決めた木の深さまで繰り返す
最後にあらかじめ決めておいた木の深さまで条件分岐を繰り返します。
先ほどの条件分岐を決めておいた木の深さまで繰り返すことで決定木が完成します。
あまり気が深すぎると過学習になり、浅すぎると分割ができないので注意が必要です。
Pythonで決定木の実行
それでは実際にPythonで決定木を実行してみましょう。
今回は以下の条件で決定木による分類を実行してみます。
| 目的変数 | アイスを買う/買わない(Buy/Not Buy) |
| 説明変数 | 天気:晴れ/曇り/雨(0/1/2) 気温:0~40℃ 同行人数:0~5 |
| 木の深さ | クロスバリデーションによって決定 |
| データ数 | 100 |
また、データセットは天気:晴れ、気温:25℃以上または天気:晴れ以外、同行人数3人以上でアイスを買うようにデータを調整しました。
それでは、実際に実行したコードを以下に紹介します。
import numpy as np
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import KFold
from sklearn import tree
import matplotlib.pyplot as plt
# データセット生成
np.random.seed(42)
# 100件のデータを生成
n_samples = 100
# 天気(晴れ、曇り、雨)、気温(0〜40℃)、同行人数(0〜5)、目的変数(アイスクリームを買うかどうか)
weather = np.random.choice([0, 1, 2], n_samples)
temperature = np.random.randint(0, 41, n_samples)
companions = np.random.randint(0, 6, n_samples)
# 天気が晴れかつ気温25℃以上、または天気が晴れ以外で同行人数が3人以上の場合にアイスクリームを買うと仮定
buy_condition = ((weather == 0) & (temperature >= 25)) | ((weather != 0) & (companions >= 3))
buy = np.where(buy_condition, 'Buy', 'Not Buy')
# データフレームの作成
data = np.column_stack((weather, temperature, companions, buy))
# 決定木モデルの構築
X = data[:, :-1] # 説明変数
y = data[:, -1] # 目的変数
# クロスバリデーションで最適な深さを求める
cv = KFold(n_splits=5, shuffle=True, random_state=42)
best_depth = None
best_score = 0
for depth in range(1, 11): # 木の深さを1から10まで試す
model = DecisionTreeClassifier(max_depth=depth, random_state=42)
scores = cross_val_score(model, X, y, cv=cv, scoring='accuracy')
mean_score = np.mean(scores)
if mean_score > best_score:
best_score = mean_score
best_depth = depth
# 最適な深さで決定木モデルを再構築
final_model = DecisionTreeClassifier(max_depth=best_depth, random_state=42)
final_model.fit(X, y)
# 決定木の可視化
plt.figure(figsize=(10, 6))
tree.plot_tree(final_model, filled=True)
plt.title('Decision Tree Regression')
plt.show()
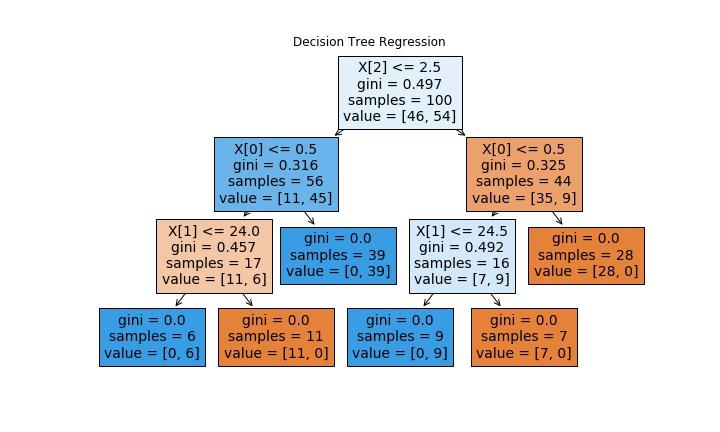
出力された決定木は上図の通りです。木の深さは3となっていますね。
一段目は同行人数が2.5人以上か?、二段目は天気が0.5以下(晴れ)か?、三段目は気温が24,24.5℃以上か?という条件分岐をしていますね。
最終的に分類されたサンプルのジニ不純度を見ると0となっているので完全に買う人、買わない人を分類できたようです。データセットを調整したので当たり前と言ってはそうですが…
以上がPythonによる決定木の実行になります。
学習ステップをさらに進めたい方へ
決定木の基本的な概念を理解したら、
次はどの基準で分岐が選ばれ、木が深くなるとなぜ過学習しやすくなるのかを、
仕組みとして整理しておきたいところです。
その理解を深め、次の学習ステップへ進むためのインプットとしておすすめなのが、
『図解即戦力 機械学習&ディープラーニングのしくみと技術がこれ一冊でしっかりわかる教科書』です。
本書は、コード実装を主目的とした実践書ではなく、
決定木を含む機械学習アルゴリズムの構造・考え方・学習の流れを、図解中心で丁寧に整理する教科書です。
難しい数式に踏み込まず、回帰・分類・クラスタリングまでを通して、
「なぜその分岐が選ばれるのか」「どこでモデルが複雑になりすぎるのか」をブラックボックス化せずに理解できます。
たとえば決定木についても、
- 不純度指標(ジニ不純度・情報利得など)が分岐にどう使われるのか
- 木の深さや最小サンプル数がモデルの表現力にどう影響するのか
- なぜ決定木は解釈しやすい一方で過学習しやすいのか
といった点を、数式やコードを追わずに概念として整理できるため、
この先ランダムフォレストやGBDTといったアンサンブル手法への理解もスムーズにつながります。
「決定木を使ってはいるが、なぜその分岐になるのか説明できない」
「次はアンサンブル学習に進みたいので、その前に仕組みを整理しておきたい」
そんな方にとって、実装フェーズへ進む前段階のインプットとして最適な一冊です。
本書で理解の土台を固めてから実装に進むことで、
“単純に当てはめる”から“構造を意識して設計する”へと学習を一段前に進められます。
一方で「Pythonはこれから…」「数式で挫折したことがある…」という方もいらっしゃるかと思います。
そんな初学者の方でもpythonで機械学習を実装できるようになるためのロードマップとオススメの教材について以下の記事にまとめていますので、興味のある方はご覧になって下さい。
終わりに
以上が決定木についての解説になります。決定木は機械学習の中でもよく使用される手法になるのでしっかりと学んでいきたいところですね。また、視覚的にもわかりやすいので、他の人に説明するときにも重宝しそうですね。次はランダムフォレストなんかも解説していきたいと思います。




コメント
[…] 決定木についてわかりやすく解説 | 化学とインフォマティクスと時々雑記, 記事https://boritaso-blog.com/dicision_tree/ […]
[…] 決定木についてわかりやすく解説 | 化学とインフォマティクスと時々雑記, https://boritaso-blog.com/dicision_tree/ […]