こんにちは!ぼりたそです!
今回は、機械学習の代表的なアルゴリズムのひとつ 「ランダムフォレスト」 について、初心者にもわかりやすく解説していきます。
この記事では、以下のポイントを中心にまとめています。
- ランダムフォレストとは?
- ランダムフォレストのメリットデメリット
- Pythonで実行
さらに、CSVデータを使って回帰モデルを構築するPythonコードも紹介していますので、実践的に学びたい方は以下の記事も合わせてご覧ください。
それでは詳細に説明していきます。
ランダムフォレストとは?
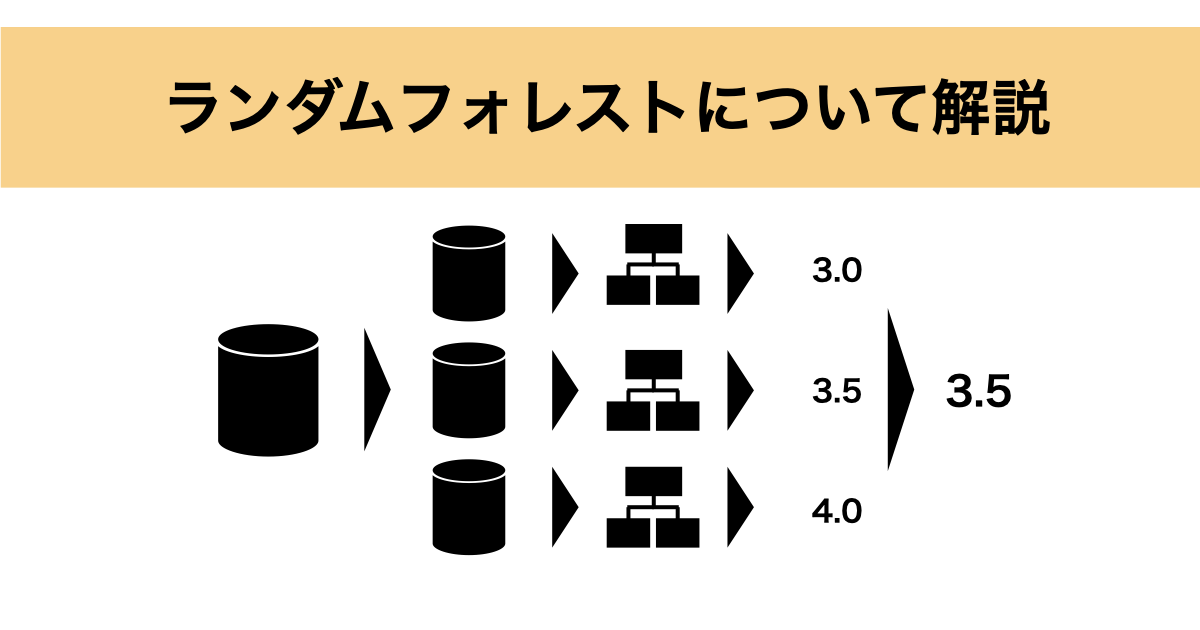
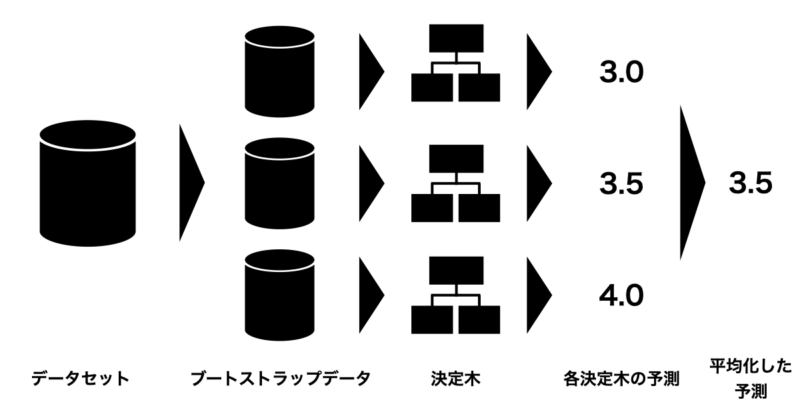
ランダムフォレスト(Random Forest) とは、複数の決定木を組み合わせて予測を行うアンサンブル学習の一手法です。
具体的には、以下のようなアルゴリズムになっています:
- 学習データからランダムにサンプリング(ブートストラップ法)して複数のデータセットを作成
- 各データセットに対して、特徴量をランダムに選びながら決定木を構築
- 各決定木の予測を集約して最終的な予測を行う
- 分類の場合:多数決でクラスを決定
- 回帰の場合:予測値の平均を算出

以下の記事で「決定木」そのものの仕組みについても解説していますので、合わせて読んでいただくと理解が深まります。
ランダムフォレストのメリット、デメリット
次にランダムフォレストのメリット、デメリットについて紹介します。
以下が具体的なメリット、デメリットになります。
■メリット
- 高い予測性能
ランダムフォレストは複数の決定木を組み合わせることで、単一の決定木よりも高い予測性能を持ちます。そのため、複雑な関係やノイズが含まれるデータに対しても強力なモデルを構築できます。
- 過学習の軽減
ブートストラップサンプリングとランダムな特徴の選択により、ランダムフォレストは比較的過学習しにくい特徴があります。
- 特徴の重要度の評価
ランダムフォレストは、決定木と同様に各特徴の重要度を評価することができます。予測モデルの安定性も高いので、重要度評価の信頼性も高いです。
次にデメリットについて以下に示します。
■デメリット
- 計算コストが高い
ランダムフォレストは数百程度の決定木を構築するため、その分計算コストが高いです。
- 過学習に対しては頑健だが、適切な調整が必要
過学習には比較的強いですが、やはり適切なハイパーパラメータの調整が必要です。特に、木の深さや木の数などを適切に設定することが重要です。
以上がランダムフォレストのメリット、デメリットになります。
きちんとデメリットを把握しつつ使用しましょう!
Pythonでの実行
それでは、実際にPythonにてランダムフォレストを実行してみたいと思います。
ここでは、簡単な一次関数をもとにしたダミーデータを用いて、ランダムフォレストによる回帰モデルを構築してみます。
条件は以下の通りです。
- 関数:$y = 2x_1 + 3x_2 + 0x_3 + 4x_4 + 0x_5 + 5x_6 + 6x_7 + 7x_8 + \varepsilon$($\varepsilon$ はノイズ項)
- 決定木の数:50個
- 予測値:ランダムに生成した10個のデータ
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.metrics import r2_score
def run_random_forest():
# 修正されたダミーデータの生成
np.random.seed(40)
X = 10 * np.random.rand(100, 8) # 0から10の範囲で100個生成
y = 2 * X[:, 0] + 3 * X[:, 1] + 0 * X[:, 2] + 4 * X[:, 3] + 0 * X[:, 4] + 5 * X[:, 5] + 6 * X[:, 6] + 7 * X[:, 7] + np.random.randn(100)
# ランダムフォレストモデルの作成と学習
model = RandomForestRegressor(n_estimators=50, random_state=40)
model.fit(X, y)
# 予測データの生成(0から10の範囲に含まれる10点)
new_data = 10 * np.random.rand(10, 8)
predicted_values = model.predict(new_data)
# 実際の関数で計算した値
actual_values = 2 * new_data[:, 0] + 3 * new_data[:, 1] + 0 * new_data[:, 2] + 4 * new_data[:, 3] + 0 * new_data[:, 4] + 5 * new_data[:, 5] + 6 * new_data[:, 6] + 7 * new_data[:, 7]
# プロット
plt.scatter(predicted_values, actual_values, label='estimated_y vs actual_y', marker='o')
plt.xlabel('estimated_y')
plt.ylabel('actual_y')
plt.legend()
# R2値の計算と表示
r2 = r2_score(actual_values, predicted_values)
print(f"\nR2値: {r2}")
# 変数の重要度の表示
feature_importances = model.feature_importances_
print("\n変数の重要度:")
for i, importance in enumerate(feature_importances):
print(f"x_{i + 1}: {importance}")
if __name__ == "__main__":
run_random_forest()
#R2値: 0.7803982290284632
#変数の重要度:
#x_1: 0.07263404624483068
#x_2: 0.035408124359172184
#x_3: 0.021419053740529888
#x_4: 0.07561376445758594
#x_5: 0.017654683212067982
#x_6: 0.16925642086437118
#x_7: 0.1840405662624788
#x_8: 0.42397334085896343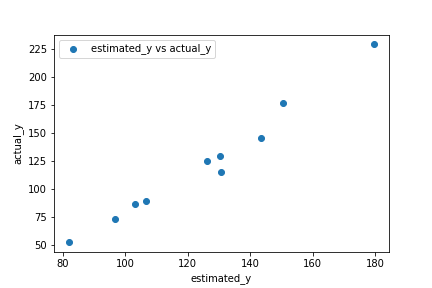

予測データ10個について実際に計算した数値と比較してy-yプロットにしました。実際の値に対してきちんと予測できていると言えます。実際に $R^2$ 値は0.78と学習モデルの性能は良好です。
また、変数の重要度を以下に示しますが、係数が重くなるにつれて変数の重要度も大きくなっていますね。係数がゼロの変数($x_3$、$x_5$)は重要度が低くなっており、モデルが正しく特徴量の影響を捉えていることがわかります。
| 変数 | 重要度 |
|---|---|
| $x_1$ | 0.073 |
| $x_2$ | 0.035 |
| $x_3$ | 0.021 |
| $x_4$ | 0.076 |
| $x_5$ | 0.018 |
| $x_6$ | 0.169 |
| $x_7$ | 0.184 |
| $x_8$ | 0.424 |
以上がPythonを用いたランダムフォレストの実装になります。
学習ステップをさらに進めたい方へ
ランダムフォレストの基本的な概念を理解したら、
次は多数の決定木を組み合わせることで、なぜ汎化性能が高まり、過学習が抑えられるのかを、
仕組みとして整理しておきたいところです。
その理解を深め、次の学習ステップへ進むためのインプットとしておすすめなのが、
『図解即戦力 機械学習&ディープラーニングのしくみと技術がこれ一冊でしっかりわかる教科書』です。
本書は、コード実装を主目的とした実践書ではなく、
ランダムフォレストを含むアンサンブル学習の考え方・構造・学習の流れを、図解中心で丁寧に解説する教科書です。
難しい数式に踏み込まず、回帰・分類・クラスタリングまでを通して、
「なぜ単体の決定木より安定した予測が得られるのか」をブラックボックス化せずに理解できます。
たとえばランダムフォレストについても、
- ブートストラップサンプリングが分散低減にどう寄与するのか
- 木の深さや本数が精度と計算コストにどう影響するのか
といった点を、数式やコードを追わずに概念として整理できるため、
この先のハイパーパラメータ設計や、他のアンサンブル手法(GBDTなど)との比較がしやすくなります。
「ランダムフォレストを使ってはいるが、なぜ安定して当たるのか説明できない」
「次はチューニングやモデル選択に進みたいので、その前に仕組みを整理しておきたい」
そんな方にとって、実装フェーズへ進む前段階のインプットとして最適な一冊です。
本書で理解の土台を固めてから実装に取り組むことで、
“とりあえず使う”から“意図して設計・調整する”へと学習を一段前に進められます。
一方で「Pythonはこれから…」「数式で挫折したことがある…」という方もいらっしゃるかと思います。
そんな初学者の方でもpythonで機械学習を実装できるようになるためのロードマップとオススメの教材について以下の記事にまとめていますので、興味のある方はご覧になって下さい。
終わりに
ランダムフォレストは、シンプルながら非常に強力な機械学習手法です。特に「決定木は分かりやすいけど精度が足りない…」と感じる方にはおすすめのアルゴリズムです。
実務でも広く活用されているので、ぜひ使い方をマスターしておきましょう!