【コード付】データ間の類似度を計算

こんにちは！ぼりたそです！

今回は「データ間の類似度」をテーマに、どのような方法で類似度を計算できるのかを紹介します。類似度の計算は、クラスタリングや異常検知など多くの機械学習の場面で重要になります。

本記事では、距離・相関・カーネルの3つの観点から代表的な手法をわかりやすく解説し、Pythonコードも交えて紹介します。

この記事は以下のポイントでまとめています。

Point

データの類似度について
　
距離に基づく類似度
　
相関に基づく類似度
　
カーネルに基づく類似度

それでは詳細に解説していきます。

データ間の類似度について
距離に基づいた類似度
1. ユークリッド距離
2. マンハッタン距離
相関に基づいた類似度の計算
1. Jaccard係数
2. コサイン類似度
カーネルに基づいた類似度の計算
終わりに

データ間の類似度について

データ間の「類似度」とは、2つのデータがどれだけ似ているかを数値的に評価するための指標です。

この概念は、クラスタリング、検索エンジン、異常検知など、さまざまな機械学習の分野で重要な役割を果たします。

類似度の計算方法にはいくつか種類がありますが、大きく分けて以下の3つに分類されます

距離に基づいた類似度
　
相関に基づいた類似度
　
カーネルに基づいた類似度

それぞれの手法について、数式やPythonコードを交えながら詳しく解説していきます。

距離に基づいた類似度

距離に基づいた類似度とは文字通りデータ間の距離から類似度を評価し、その距離が近いほどデータ同士が似ているということになります。

距離に基づいた類似度について、今回は以下の手法についてご紹介します。

ユークリッド距離
　
マンハッタン距離

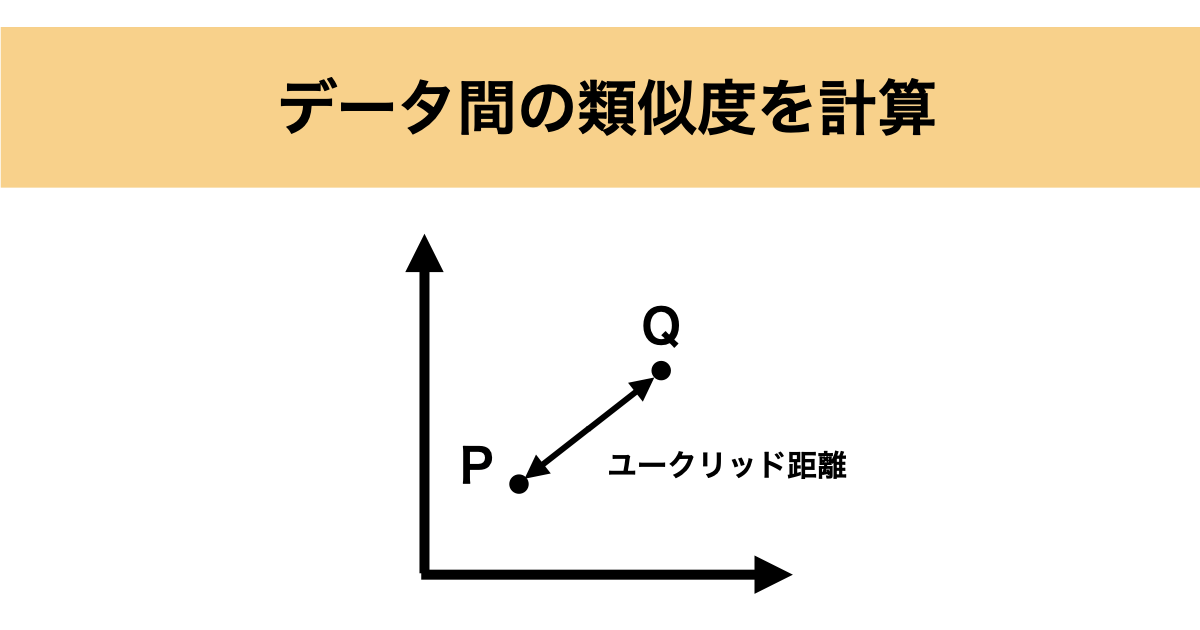
ユークリッド距離

ユークリッド距離（Euclidean distance）は、最も基本的な距離の測り方で、2点間の直線距離（最短距離）を計算します。
数値が小さいほど、2つのデータは「近い（＝類似している）」と判断できます。

二次元空間におけるイメージ図は以下の通りです。

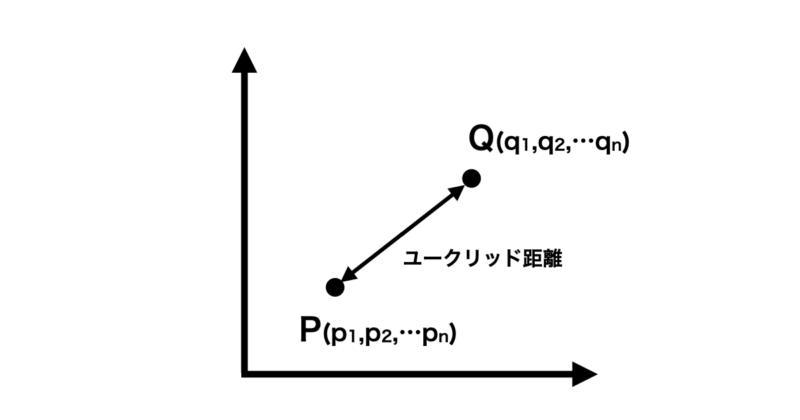
$n$次元空間内の2つの点 $p$ と$p$ の間の距離を次のように定義します

$$ \text{distance}(p, q) = \sqrt{\sum_{i=1}^{n} (p_i – q_i)^2} $$

ここで、 $p$ と $q$ はそれぞれ2つの点を表し、$n$ は次元数を表します。また、$p_i$ と $q_i$ はそれぞれ点 $p$ と $q$ の $i$ 番目の次元の座標を表します。

ユークリッド距離を計算するPythonコードも作成してみました。コードとしては簡単なものになっています。

import numpy as np

def euclidean_distance(p, q):
    """
    2つの点pとq間のユークリッド距離を計算します。
    
    :param p: ポイントpの座標を表すnumpy配列
    :param q: ポイントqの座標を表すnumpy配列
    :return: 2つの点間のユークリッド距離
    """
    return np.sqrt(np.sum((p - q)**2))

# 例として2次元の点を使用して距離を計算する
point_p = np.array([1, 2])
point_q = np.array([4, 6])

distance = euclidean_distance(point_p, point_q)
print("ユークリッド距離:", distance)

マンハッタン距離

次はマンハッタン距離について説明します。

マンハッタン距離（Manhattan distance）は、碁盤目状の道を移動するような距離の測り方で、水平方向と垂直方向の移動量の合計として表されます。都市の道路やグリッド状の構造を考える際によく使われます。

この距離が短いとデータ間の類似度が高いと言えます。

二次元空間上におけるイメージ図は以下の通りです。

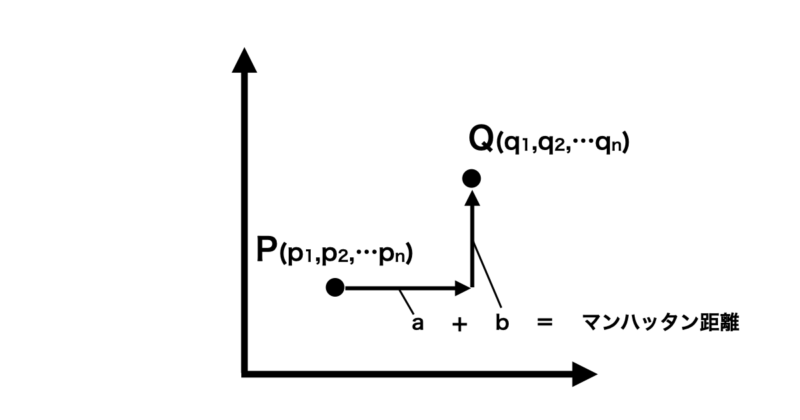
マンハッタン距離は、以下のような定義式で表されます。

$$ \text{distance}(p, q) = \sum_{i=1}^{n} |p_i – q_i| $$

マンハッタン距離は、ユークリッド距離と異なり、直線距離ではなくグリッド上を移動する際の距離を表現するため、実生活の問題においても有用です。
例えば、都市の地図上で2つの場所間の移動距離を計算する場合などに利用されます。

マンハッタン距離を算出するPythonコードを作成したので、以下に記載しておきます。

import numpy as np

def manhattan_distance(p, q):
    """
    2つの点pとq間のマンハッタン距離を計算します。
    
    :param p: ポイントpの座標を表すnumpy配列
    :param q: ポイントqの座標を表すnumpy配列
    :return: 2つの点間のマンハッタン距離
    """
    return np.sum(np.abs(p - q))

# 例として2次元の点を使用して距離を計算する
point_p = np.array([1, 2])
point_q = np.array([4, 6])

distance = manhattan_distance(point_p, point_q)
print("マンハッタン距離:", distance)

相関に基づいた類似度の計算

次に相関に基づいた類似度の計算について紹介します。

相関に基づいた類似度の計算手法は単純なデータ間の距離ではなく、傾向などから相関性を算出して類似度を計算することが特徴です。

具体的には以下の計算手法について解説していきます。

Jaccard係数
　
コサイン類似度

Jaccard係数

まずはJaccard係数について説明していきます。

Jaccard係数は、集合データ同士の「重なり具合（共通性）」を評価するための指標です。
2つの集合がどれだけ要素を共有しているかを、0〜1の値で表現します。

Jaccard係数が1に近づくほどデータは似ていることになります。

イメージ図としては以下の通りになります。

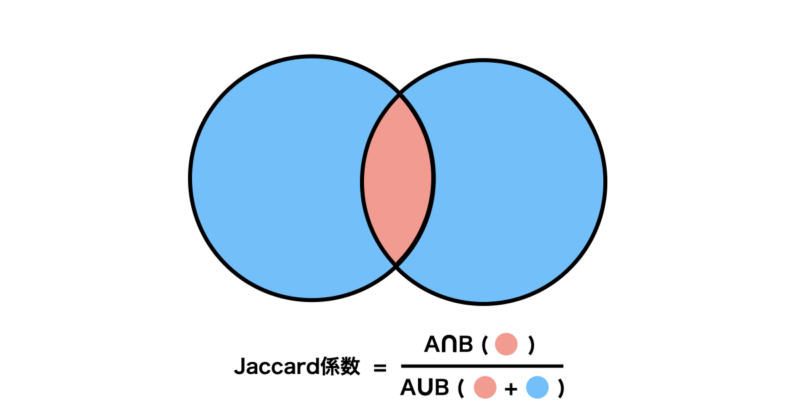
また定義式は以下のようになります。

$$J(A, B) = \frac{|A \cap B|}{|A \cup B|}$$

簡単にですが、PythonにてJaccard係数を算出するコードを作成しましたので、記載します。

def jaccard_similarity(set1, set2):
    """
    2つの集合のJaccard係数を計算します。
    
    :param set1: 集合1
    :param set2: 集合2
    :return: Jaccard係数
    """
    intersection = len(set1.intersection(set2))
    union = len(set1.union(set2))
    return intersection / union if union != 0 else 0

# 例として、2つの集合を定義してJaccard係数を計算する
set1 = {1, 2, 3}
set2 = {2, 3, 4}

jaccard_coefficient = jaccard_similarity(set1, set2)
print("Jaccard係数:", jaccard_coefficient)

コサイン類似度

次にコサイン類似度について説明します。

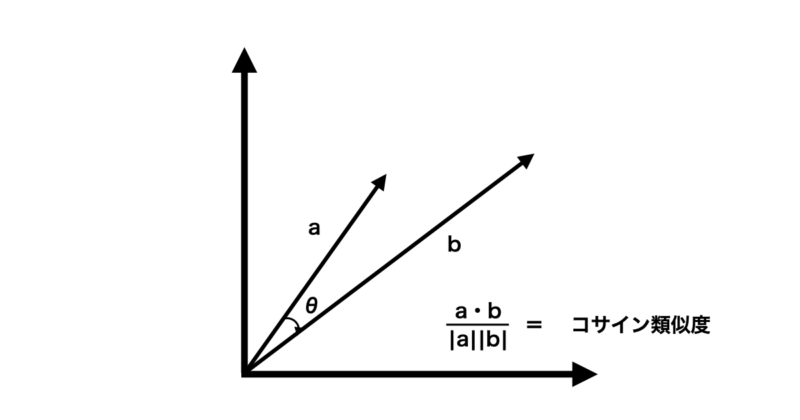
コサイン類似度（Cosine similarity）は、2つのベクトルの「向きの一致度」を測定する指標です。
大きさではなく、角度（方向性）に注目するため、文章や画像の特徴ベクトルの比較によく使われます。

値は $-1$ 〜 $1$ の範囲をとり、1に近いほど方向が一致している（＝類似している）ことを示します。

下にコサイン類似度の定義式とイメージ図を示します。

2つのベクトル a, bのコサイン類似度 sim(a,b) は、ベクトルの内積をベクトルのノルム（長さ）の積で割ることによって計算されます。

$$ \text{sim}(\mathbf{a}, \mathbf{b}) = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|} $$

また、Pythonにてコサイン類似度を算出するコードを作成しました。

import numpy as np

def cosine_similarity(vector1, vector2):
    """
    2つのベクトル間のコサイン類似度を計算します。
    
    :param vector1: ベクトル1
    :param vector2: ベクトル2
    :return: コサイン類似度
    """
    dot_product = np.dot(vector1, vector2)
    norm_vector1 = np.linalg.norm(vector1)
    norm_vector2 = np.linalg.norm(vector2)
    
    if norm_vector1 == 0 or norm_vector2 == 0:
        return 0
    
    return dot_product / (norm_vector1 * norm_vector2)

# 例として、2つのベクトルを定義してコサイン類似度を計算する
vector1 = np.array([1, 2, 3])
vector2 = np.array([4, 5, 6])

cosine_sim = cosine_similarity(vector1, vector2)
print("コサイン類似度:", cosine_sim)

カーネルに基づいた類似度の計算

最後にカーネルに基づいた類似度の計算についてご紹介します。

カーネルについては以前記事にまとめたので、ご参考いただければと思います。
カーネルはデータがどれだけ似ているかの指標と思っていただければ問題ないかと思います。

合わせて読みたい

カーネルを使用した場合、通常、カーネル関数の値に基づいて計算されます。

今回はよく使用されるカーネル関数としてRBFカーネル（ガウシアンカーネル）についてご紹介します。

RBFカーネルはその値が1に近いほど、2つのデータは類似していると見なされます。

定義式は以下のようになっています。

$$\text{RBF}(x, y) = \exp\left(-\gamma \cdot |x – y|^2\right) $$

式としてはユークリッド距離$ |x – y|^2 $にハイパーパラメータ$ \gamma\ $をかけた指数関数になっています。ベースとしてはユークリッド距離と同じで距離が近いほどデータが似ていることになります。

また、PythonにてRBFカーネルを使用して類似度を計算するコードを作成しました。

import numpy as np

def rbf_kernel_similarity(x1, x2, gamma=1.0):
    """
    2つのデータポイント間のRBFカーネルを使用した類似度を計算します。
    
    :param x1: データポイント1
    :param x2: データポイント2
    :param gamma: RBFカーネルのパラメータ（デフォルト値は1.0）
    :return: RBFカーネルを使用した類似度
    """
    distance = np.linalg.norm(x1 - x2)  # ユークリッド距離の計算
    similarity = np.exp(-gamma * distance**2)  # RBFカーネル関数の適用
    return similarity

# 例として、2つのデータポイントを定義し、RBFカーネルを使用した類似度を計算する
data_point1 = np.array([1, 2, 3])
data_point2 = np.array([1, 1, 3])

rbf_similarity = rbf_kernel_similarity(data_point1, data_point2)
print("RBFカーネルを使用した類似度:", rbf_similarity)