こんにちは!ぼりたそです!今回はベイズ最適化における獲得関数についてまとめた記事を作成しました。
この記事は以下のポイントでまとめています。
- なぜ獲得関数が必要なのか?
- 獲得関数とは?
- 各種獲得関数の特徴
- 獲得関数ごとの探索数比較
- オススメの書籍
それでは詳細にご説明していきます。
なぜ獲得関数が必要なのか?
ベイズ最適化では、ガウス過程回帰により「ある点での予測値(平均値)」と「予測の不確かさ(分散)」を推定できます。
しかし、単に平均値が一番高いところだけを試していくと、次第に局所解にハマってしまう可能性があります。
そこで、
- 期待できる(高い値が出そう)
- 未知の場所を探索する(分散が大きい)
という両方をバランスよく考えながら、次の探索点を決める必要があるのです。
この「どこを探すかを数式で賢く決める役割」を担うのが獲得関数です。
獲得関数とは?
獲得関数について具体例を用いて詳細を説明いたします。
先述の通り、獲得関数とはベイズ最適化においてガウス過程回帰で得られた平均と分散から表せる関数であり、次の候補点を決める指標です。
例として $y=sin(x)$ に従う5点を学習データとしてガウス過程回帰を行った結果を下にグラフとして示します。
ガウス過程回帰からグラフのように平均値(黒線)と分散(青帯)が表されています。
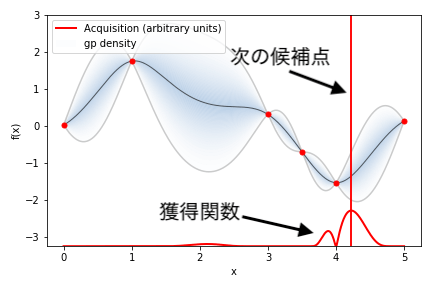
獲得関数はこの平均値と分散から探索領域を評価して、最も期待できる候補点を決める指標となってくれます。
上のグラフではyの最小化を目標として獲得関数が赤線として示されており、最も評価が高い点を次の候補点として決めることができます。
獲得関数の種類と特徴
察しがつく方もいるかと思いますが、獲得関数はいくつか種類があり、目的に応じて使い分けることができます。
代表的な獲得関数は以下の通りです。
- PI(Probability of Improvement)
- PTR(Probability in Target Range)
- EI(Expected Improvement)
- UCB/LCB(Upper/Lower Confidence Bound)
PI(Probability of Improvement)
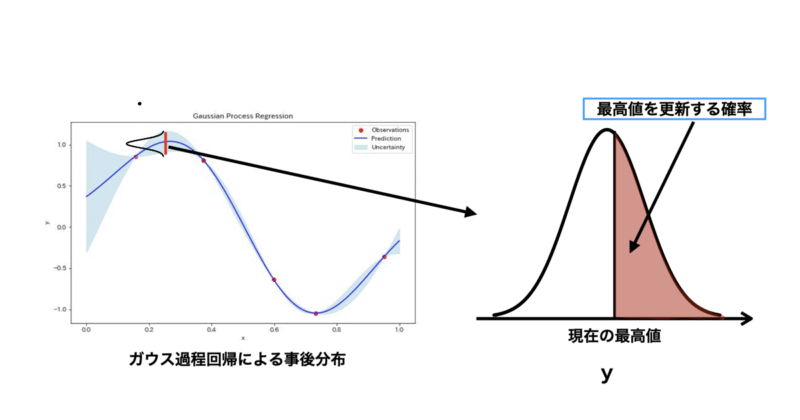
PIは現状の最大値(最小値)を更新する確率を表しています。
図を上に示していますが、ある特徴量Xが与えるYがガウス過程回帰による事後分布で表されるとき、ある点X1において右上のようにY1が正規分布で表せるとすると赤枠の領域がPIになります。
PIの特徴としては先述の通り最大値を更新する確率の高い候補を選択する点が挙げられます。それ故に現状の最大値付近の候補を選択しやすく、局所最適解に陥りやすいとも言えるので注意が必要ですね。
幅広い領域を「探索」するというよりは今あるデータを「活用」する関数と言えるでしょう。
PTR(Probability in Target Range)
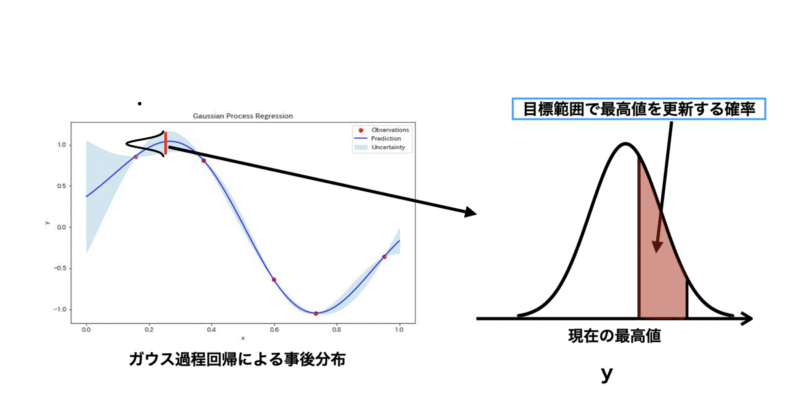
PTRはPIの派生型のような獲得関数になります。PIは現状の最大値を超える確率を表していますが、PTRはある範囲内で最高値を超える確率を表しています。
図にすると上のようになり、赤枠で囲った領域がPTRを表しています。
PTRもPIと同様に幅広い領域を「探索」するというよりは今あるデータを「活用」する関数と言えます。また、局所最適解に陥りやすいというデメリットもあるので注意が必要です。
EI(Expected Improvement)
EIは最大値の改善値の期待値から次の候補点を選択します。つまり、改善の「量」と「確率」を掛け合わせて最大のところを探すということですね。
PIやPTRと似ている気がしますが、PIやPTRは最大値を更新する確率を表すのに対してEIは最大値を更新する期待値を表します。
しかし、学習データの改善を目的とした関数としてはPIやPTRと同様であり、探索の幅が狭くなりがちなため局所最適解に陥る可能性もあります。
UCB/LCB(Upper/Lower Confidence Bound)
UCB/LCBは探索と活用を使い分けできる獲得関数となっています。具体的には以下のようにガウス過程回帰から得られる予測平均値と予測標準偏差を足す/引くことで計算しています。
UCB(x) = μ(x) + κσ(x)
LCB(x) = μ(x) – κσ(x)
μ(x)は平均値、σ(x)は分散、κはハイパーパラメータとなっており任意の値とすることができます。UCBは分散を加算することで最大化を目指し、LCBは分散を引くことで最小化を目指すことができます。
また、κの値が大きければ分散値の重みが大きくなり「探索」の傾向が強くなります。逆にκが小さければ平均値の重みが大きくなり「活用」傾向が強くなります。「探索」も「活用」もできる器用な関数と言えるでしょう。
獲得関数ごとの探索数比較
それでは実際に獲得関数ごとに探索数がどの様に変わるか実証してみます。
今回は以下の関数の最大化を目指していきます。最大点はx=0になります。
$$f(x) = \sin(x) \cdot \cos(x) \cdot x^{-1}$$
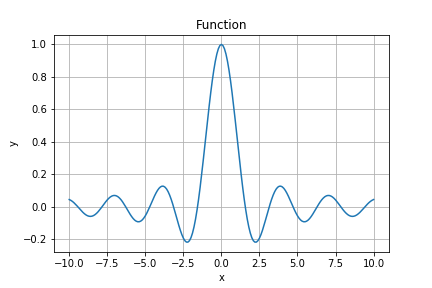
使用する獲得関数はEI、PI、LCBの3つになります。下記コードのacquisition_typeで獲得関数を選択しています。
最適化はGPyOptというPythonライブラリを使用して行いました。
※プログラムの都合上、-f(x)を最小化することで最適化をおこなっています。
import GPy
import GPyOpt
import numpy as np
import matplotlib.pyplot as plt
trial = 1
# -2から2まで0.1刻みの数値を含む配列を作成
pre_x = np.arange(-7, -4, 0.2)
pre_x = pre_x.reshape(-1,1)
# 関数の計算
pre_y = np.cos(pre_x) * pre_x**-1 * np.sin(pre_x) # 例としてsin関数を使用
pre_y = pre_y.reshape(-1,1)
# 目的関数の定義
def objective_function(x):
global pre_y, pre_x, trial
print(f'trial : {trial}')
trial += 1
#候補のxを出力して学習データに追加する
print('x :',x)
pre_x = np.append(pre_x,x)
pre_x = pre_x.reshape(-1,1)
#候補のxからyを計算して学習データに追加する
y = np.cos(x) * x**-1 * np.sin(x)
print('y :',y)
pre_y = np.append(pre_y,y)
pre_y = pre_y.reshape(-1,1)
return y
# 定義域の設定
domain = [{'name': 'x', 'type': 'continuous', 'domain': (-10, 10)}]
# BayesianOptimizationオブジェクトの作成
bo = GPyOpt.methods.BayesianOptimization(f=objective_function,
model_type='GP',
domain=domain,
acquisition_type='MPI',#EI or MPI or LCB
maximize = True,
X=pre_x,
Y=pre_y)
# ベイズ最適化の実行(yが0.99以上になるまで繰り返す)
while np.max(pre_y)<0.99:
# 1つの候補点を出力
bo.run_optimization(max_iter=1)
bo.plot_acquisition(f'graph_{trial}.png')#ガウス過程回帰のプロットと獲得関数のグラフを表示
#plt.savefig(f'graph_{trial}.png')
結果は…
■EI(9回)
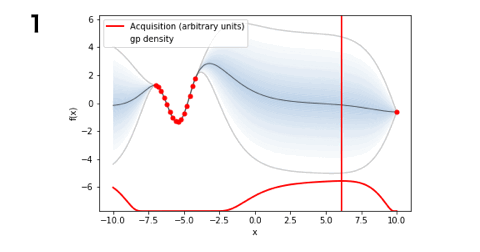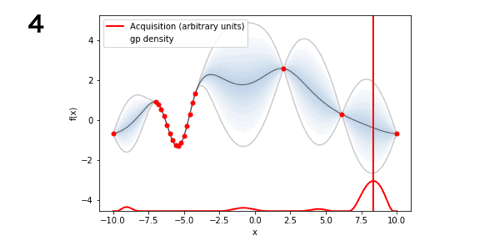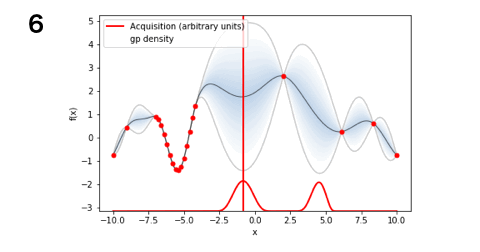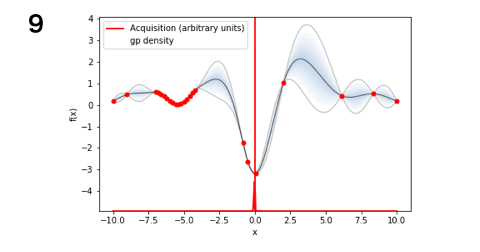
■PI(14回)
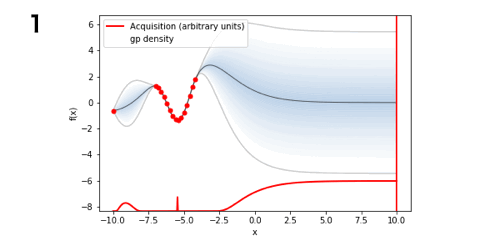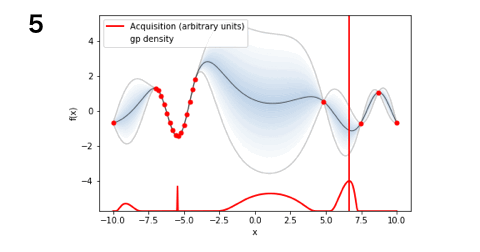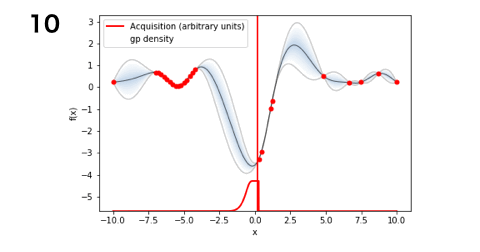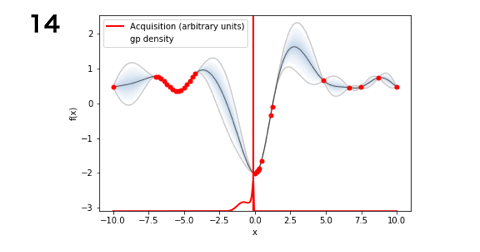
■LCB(5回)
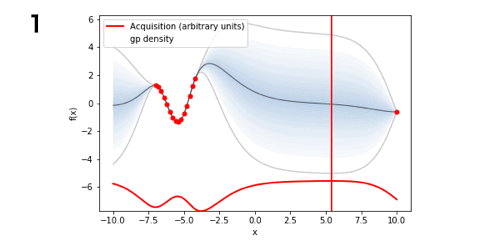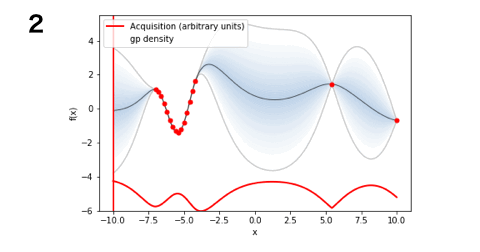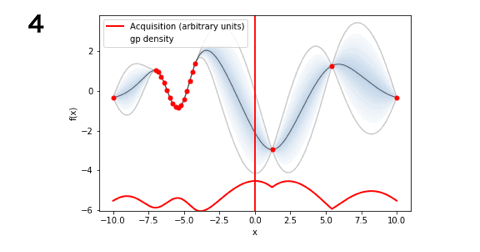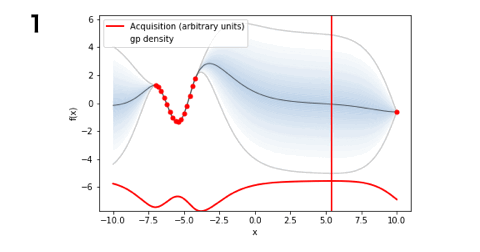
となりました!今回のお題ではLCBが一番探索数が少なく最適解にたどり着くことができましたね。
どの獲得関数が適しているかはその課題によって異なりますので、獲得関数の特徴を踏まえて選択する様にしましょう!
オススメの書籍
最後に、獲得関数やベイズ最適化についてさらに深く学びたい方に向けて、オススメの書籍をご紹介します。
ご紹介する
『Pythonで学ぶ実験計画法入門 ベイズ最適化によるデータ解析』
は、特に材料開発やプロセス開発における実験計画法に焦点を当てた、非常に実践的な内容となっています。
本書の特徴として
- ベイズ最適化の基本概念の解説
- 獲得関数やガウス過程回帰の詳細な解説
- 実際に使えるPythonコードとデータセットをGitHubからダウンロード可能
という点から、実際に手を動かしながらベイズ最適化を学ぶことができ理解がぐっと深まります。
特に、材料やプロセスの最適化を効率的に進めたいと考えている方には、本書のアプローチは非常に実用的で、すぐに現場に活かせる内容だと感じました。
さらに、ベイズ最適化以外にも、機械学習を活用したデータ解析手法について幅広く解説されているため、実験設計からデータ解析まで一貫して学びたい方にもぴったりです。
材料開発の現場で、データを最大限に活用したいと考えている方に、ぜひ手に取っていただきたい一冊です。
ベイズ最適化のオススメ参考書については以下の記事でもまとめていますので、興味のある方は参照いただければと思います。
終わりに
いかがでしたでしょうか。それぞれの獲得関数でも目的や表す数値がかなり違うことがわかると思います。ベイズ最適化は学習データが少ないうちは「探索」して、ある程度目星が付いたら「活用」に切り替えると試行回数が回数が少なくすむとも言われています。場合分けして適切な獲得関数を使えるようにしたいですね。