【コード付】PHYSBOで多目的最適化を実装

こんにちは！ぼりたそです！

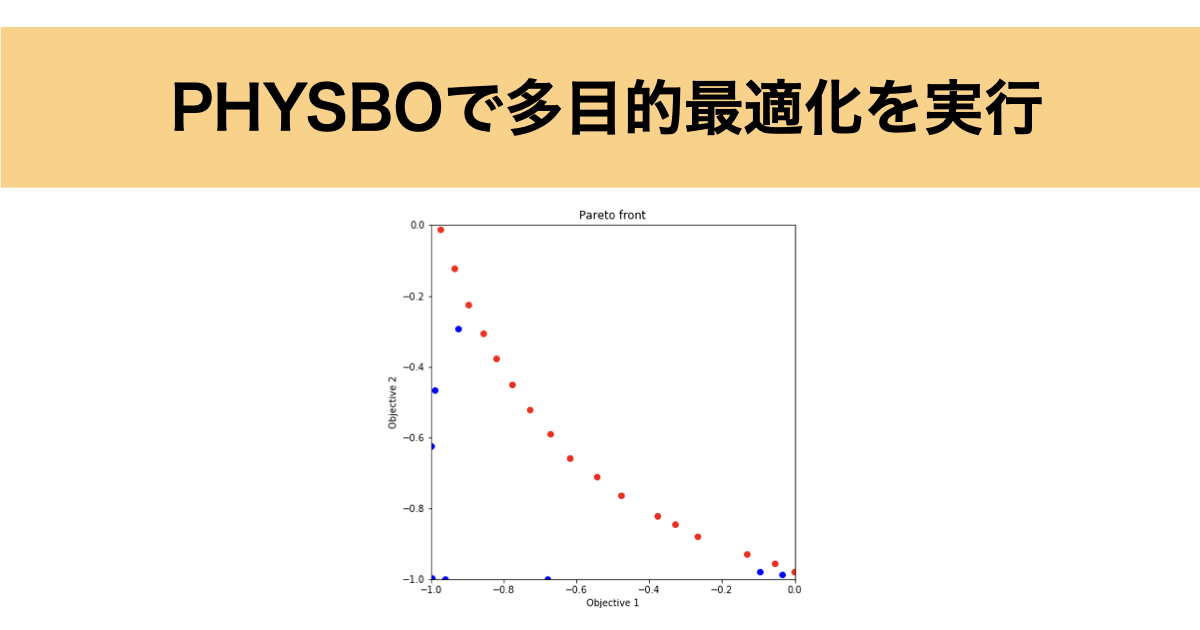
今回はPHYSBOで多目的最適化を実行したので、その実装方法について解説していきます！

この記事は以下のポイントでまとめています。

Point

PHYSBOとは
　
多目的最適化フロー
　
実行コードとその解説

以前、PHYSBOで単目的最適化を実装した記事がありますので、ご興味ある方は以下の記事を参照いただければと思います。

合わせて読みたい

それでは詳細に解説していきます。

PHYSBOについて
多目的最適化の条件
実行コード
コードの解説
終わりに

PHYSBOについて

PHYSBO(optimization tool for PHYSics based on Bayesian Optimization)は、高速でスケーラブルなベイズ最適化のためのPythonライブラリとなっています。

このライブラリは東京大学物性研究所をはじめとしたチームによって開発されています。

詳しくは以下の公式ドキュメントを参照いただければと思います。
https://issp-center-dev.github.io/PHYSBO/manual/master/ja/introduction.html

一般的なベイズ最適化では計算コストが大きく、scikit-learnなどでベイズ最適化を実行する場合は多くのデータを扱うのは困難であるのに対してPHYSBOは以下の特徴により高いスケーラビリティを実現しているそうです。

Thompson Sampling
　
random feature map
　
one-rank Cholesky update
　
automatic hyperparameter tuning

多目的最適化の条件

次に多目的最適化の条件について説明していきます。

今回はPHYSBOチュートリアルに記載されているサンプルコードを使用して多目的最適化を実行していきたいと思います。

具体的な多目的最適化の条件としては以下のテーブルの通りとなります。

目的関数	VLMOP2
探索範囲	0 ≦ x ≦ 1
目標	パレート解の到達
初期データ数	5
学習モデル	ガウス過程回帰
カーネル	RBF
獲得関数	HVPI

まず、最適化する関数についてですが、多目的最適化のベンチマーク関数であるVLMOP2を使用してパレート解を求めていきます。関数としては以下の様になっています。

$$f_1(x) = 1 – \exp \left( -\sum_{i=1}^{i} \left( \frac{{x_i – 1}}{{\sqrt{N}}} \right)^2 \right)$$

$$f_2(x) = 1 – \exp \left( -\sum_{i=1}^{i} \left( \frac{{x_i + 1}}{{\sqrt{N}}} \right)^2 \right)$$

多目的最適化のベンチマーク関数はいくつか知られており、ZDTやDTLZなど色々あるのでそれぞれで試してみてもいいかもしれませんね。

以下にVLMOP2である二つの関数の値をグリッド状にプロットした結果になります。Y軸が$f_2(x)$, X軸が$f_1(x)$を表しています。

赤くプロットされている箇所がパレート解となっており、凹型のパレート解を有していることがわかりますね。

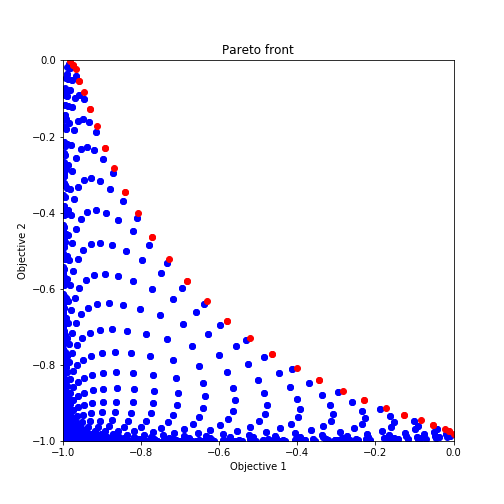
この赤い点まで到達することが今回の目標になります。

また学習モデルとカーネルについては単目的最適化と同様にガウス過程回帰を使用しています。

獲得関数は

実行コード

次に実際に多目的最適化を実行したコードとその結果を見ていきましょう。

多目的最適化を実行したコードは以下の通りです。

import numpy as np
import matplotlib.pyplot as plt
import physbo
import itertools
%matplotlib inline

#関数の定義
def vlmop2_minus(x):
    n = x.shape[1]
    y1 = 1 - np.exp(-1 * np.sum((x - 1/np.sqrt(n)) ** 2, axis = 1))
    y2 = 1 - np.exp(-1 * np.sum((x + 1/np.sqrt(n)) ** 2, axis = 1))

    return np.c_[-y1, -y2]

#探索範囲の定義
a = np.linspace(0,2,101)
test_X = np.array(list(itertools.product(a, a)))

#simulatorの定義
class simulator(object):
    def __init__(self, X):
        self.t = vlmop2_minus(X)

    def __call__( self, action):
        return self.t[action]

simu = simulator(test_X)

#policyの設定
policy = physbo.search.discrete_multi.policy(test_X=test_X, num_objectives=2)
policy.set_seed(0)

#ランダムサーチの実行
res_random = policy.random_search(max_num_probes=5, simulator=simu)

#ベイズ最適化の実行
res_HVPI = policy.bayes_search(max_num_probes=20, simulator=simu, score='HVPI', interval=10)

結果は以下のコードにて出力しています。

def plot_pareto_front(res):
    global i
    front, front_num = res.export_pareto_front()
    dominated = [i for i in range(res.num_runs) if i not in front_num]
    points = res.fx[dominated, :]

    plt.figure(figsize=(7, 7))
    plt.scatter(res.fx[dominated,0], res.fx[dominated,1], c = "blue")
    plt.scatter(front[:, 0], front[:, 1], c = "red")
    plt.title('Pareto front')
    plt.xlabel('Objective 1')
    plt.ylabel('Objective 2')
    plt.xlim([-1.0,0.0])
    plt.ylim([-1.0,0.0])
    plt.savefig(f'pareto_{i}.png')

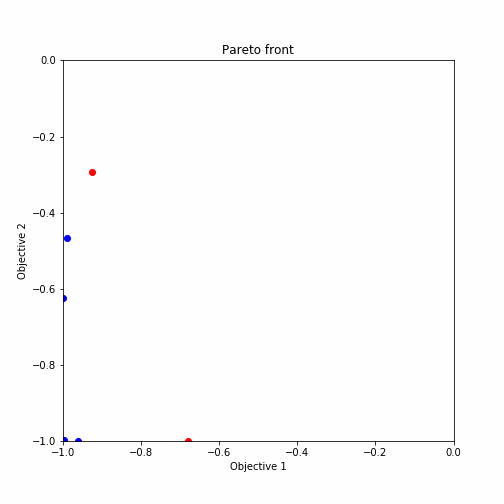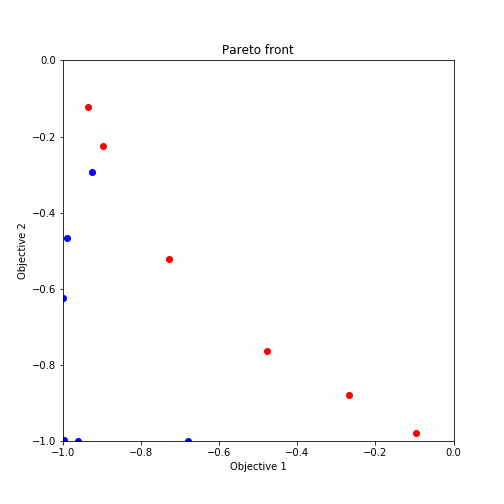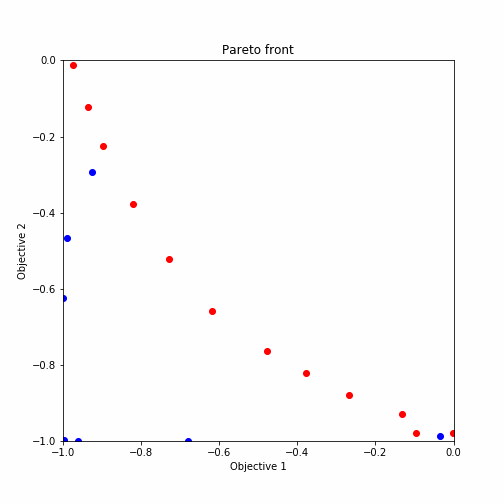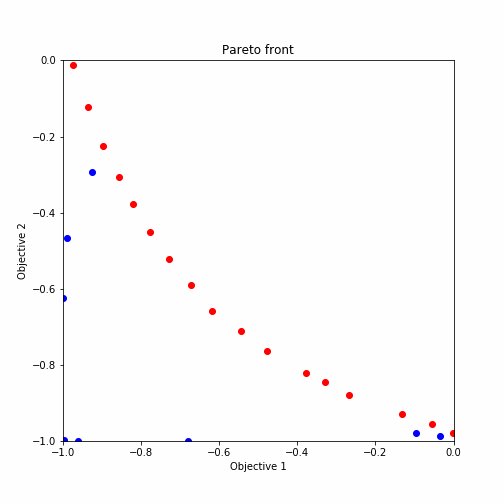
plot_pareto_front(res_HVPI)

出力結果をgifアニメーションにした結果が以下の通りとなります。

ランダムサーチ後の多目的最適化からのプロットを示しており、赤いプロットがパレート解になっています。ほとんどがパレート解を引き当てていますね。

コードの解説

それでは実装したコードの解説をしていきます。

多目的最適化を実行する手順としては以下の通りとなります。

関数の定義
　
探索範囲の定義
　
simulatorの定義
　
policyの設定
　
ランダムサーチ
　
ベイズ最適化
　
結果の出力

それでは順番に解説していきます。

関数の定義

まずは関数の定義についてです。

今回のコードでは以下の部分で目的関数（VLMOP2）の定義を行なっています。

#関数の定義
def vlmop2_minus(x):
    n = x.shape[1]
    y1 = 1 - np.exp(-1 * np.sum((x - 1/np.sqrt(n)) ** 2, axis = 1))
    y2 = 1 - np.exp(-1 * np.sum((x + 1/np.sqrt(n)) ** 2, axis = 1))

    return np.c_[-y1, -y2]

特に難しいことはありませんが、説明変数を引数xとして渡すことでy1, y2を計算して-y1, -y2としてnumpy行列で返す関数になっています。

関数の値に-1が掛けられているのは最小化を目的としているからです。

ちなみにnp.c_は配列を結合するメソッドになります。今回ではy1, y2を結合しているわけですね。

探索範囲の定義

次に探索範囲の定義について説明します。

今回のコードでは以下の部分で実行しています。

#探索範囲の定義
a = np.linspace(-2,2,101)
test_X = np.array(list(itertools.product(a, a)))

今回は探索範囲を0≦x≦1で設定しており、np.linspaceで0から1を101分割にしています。

その後、itertools.productにより101×101のnumpy配列を作成してx1,x2の全ての組み合わせを網羅できる様にしています。

simulatorの定義

次にsimulatorの定義について説明していきます。

今回のコードでは以下の部分で実行しています。

#simulatorの定義
class simulator(object):
    def __init__(self, X):
        self.t = vlmop2_minus(X)

    def __call__( self, action):
        return self.t[action]

simu = simulator(test_X)

まずは__init__関数によりxから算出したVLMOP2関数の結果を返します。

その後、__call__関数により次の候補となる値を取得します。actionは次の候補となるxの組み合わせのインデックス番号になっています。

policyの設定

次にpolicyの設定について説明します。

今回のコードでは以下の部分で実行しています。

#policyの設定
policy = physbo.search.discrete_multi.policy(test_X=test_X, num_objectives=2)
policy.set_seed(0)

このコードでは最適化の設定を行なっており、引数test_Xには探索範囲のndarrayを設定します。

今回は二つの関数の最適化になるのでnum_objectivesは2で設定しています。

ランダムサーチの実行

次にランダムサーチの実行について説明します。

今回のコードでは以下の部分で実行しています。

#ランダムサーチの実行
res_random = policy.random_search(max_num_probes=5, simulator=simu)

max_num_probesには一度に探索を行う回数を設定し、simulatorには定義したsimulatorを設定します。

このランダムサーチで取得したデータがベイズ最適化の初期データになります。

ベイズ最適化の実行

次にベイズ最適化の実行について説明していきます。

今回のコードでは以下の部分で実行しています。

#ベイズ最適化の実行
res_HVPI = policy.bayes_search(max_num_probes=20, simulator=simu, score='HVPI', interval=10)

設定したpolicyからベイズ最適化を実行するメソッドを呼び出します。

設定する引数については以下の通りとなります。

引数	設定値
max_num_probes	一度に行う探索数
simulator	定義したsimulatorクラス
score	獲得関数（TS, HVPI, EHVIから選択）
interval	ハイパーパラメータの学習を行う間隔。 0にした場合は最初の一回のみ学習する。

結果の出力

最後に結果の出力について説明します。

今回のコードでは以下の部分で実行しています。

def plot_pareto_front(res):
    global i
    front, front_num = res.export_pareto_front()
    dominated = [i for i in range(res.num_runs) if i not in front_num]
    points = res.fx[dominated, :]

    plt.figure(figsize=(7, 7))
    plt.scatter(res.fx[dominated,0], res.fx[dominated,1], c = "blue")
    plt.scatter(front[:, 0], front[:, 1], c = "red")
    plt.title('Pareto front')
    plt.xlabel('Objective 1')
    plt.ylabel('Objective 2')
    plt.xlim([-1.0,0.0])
    plt.ylim([-1.0,0.0])
    plt.savefig(f'pareto_{i}.png')

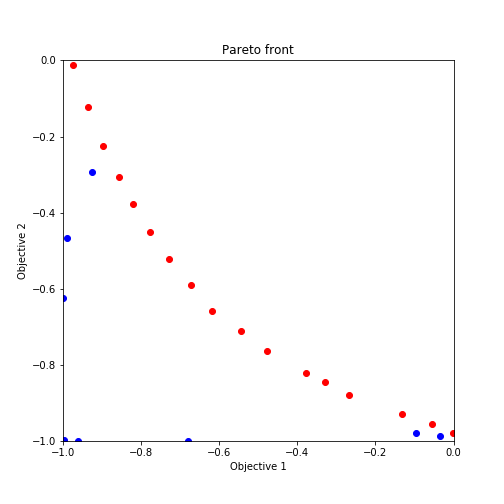
plot_pareto_front(res_HVPI)

探索した候補点について二つの関数を軸としたグラフにプロットされるように設定されています。また、パレート解については赤くプロットされる様になっています。

出力されたグラフは以下のような形式になります。