こんにちは、ぼりたそです!
この記事では、分類問題(classification)で用いられる主要な評価指標について、それぞれの意味・数式・使いどころを丁寧に解説します。
この記事は以下のポイントでまとめています。
- 二値分類の評価指標
- 正答率(accuracy)と誤答率(Error Rate)
- 適合率(precision)と再現率(recall)
- F1 scoreとF$\beta$ score
- Logloss
- 多クラス分類問題
- multi-class accuracy
- multi-class Logloss
- mean F1, micro F1, macro F1
- Quadratic Weighted Kappa
それでは順に説明していきます。
二値分類(Binary Classification)
まずは、出力が「Positive / Negative」の2値(例:スパム or 非スパム、病気あり or なし)の場合に使用される評価指標について説明します。
二値分類モデルの予測結果は、混同行列(Confusion Matrix)として以下のように表現されます。
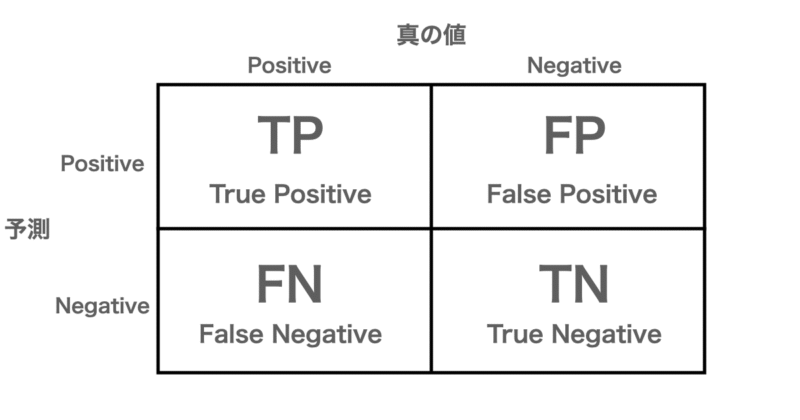
この4つの数値から、多様な指標を導けます。
正答率(Accuracy)と誤答率(Error Rate)
- 正答率(Accuracy):
最も基本的な評価指標で、「全体の中でどれくらい正しく分類できたか」を示します。
$$\text{Accuracy} = \frac{TP + TN}{TP + FP + FN + TN}$$
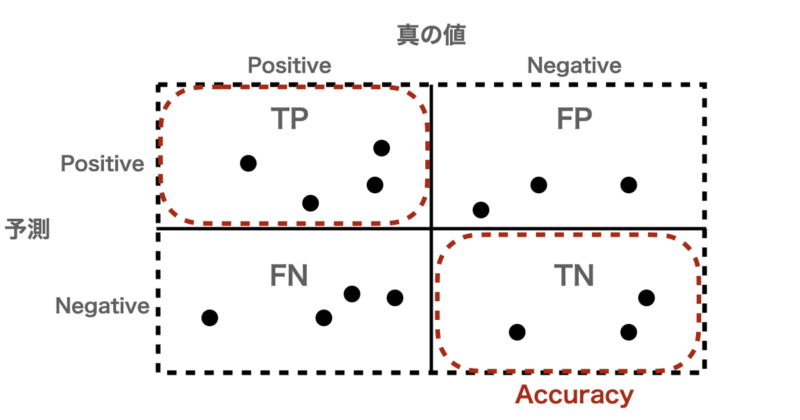
例として、下の図からAccuracyは
$$\text{Accuracy} = \frac{4 + 3}{4 + 3 + 4 + 3} = 0.5$$
- 誤答率(Error Rate):
誤答率(Error Rate)はAccuracyの逆で、「全体でどれくらい誤って分類してしまったか」を示します。
$$\text{Error Rate} = 1 – \text{Accuracy}$$
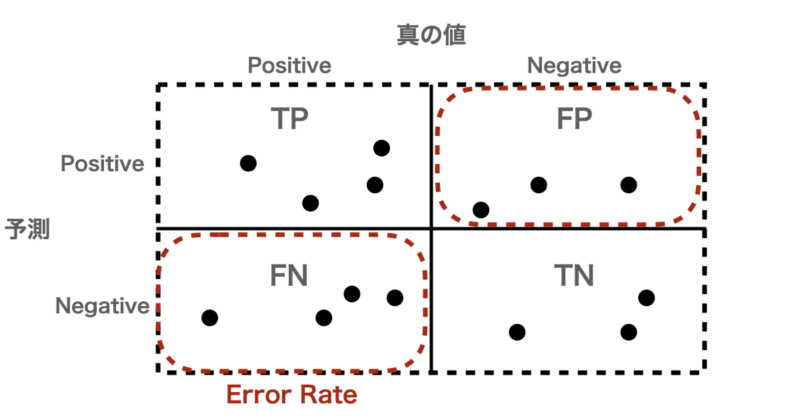
例として、下の図からError Rateは
$$\text{Error Rate} = 1 – 0.5 = 0.5$$
◼️ 特徴・使いどころ
データのクラス比がおおむね均等なときに有効な指標になります。一方で不均衡データでは偏りが出やすくなります。例えば、データの内訳として陽性1%、陰性99%の場合、常に「陰性」と予測しても Accuracy = 0.99 になってしまいます。
◼️ 注意点
先述のとおり、Accuracy が高くてもデータの偏りによっては「本当に検出したいクラス(陽性)」をうまく当てているとは限りません。そのため、後述の Precision や Recall が重要になります。
適合率(Precision)と再現率(Recall)
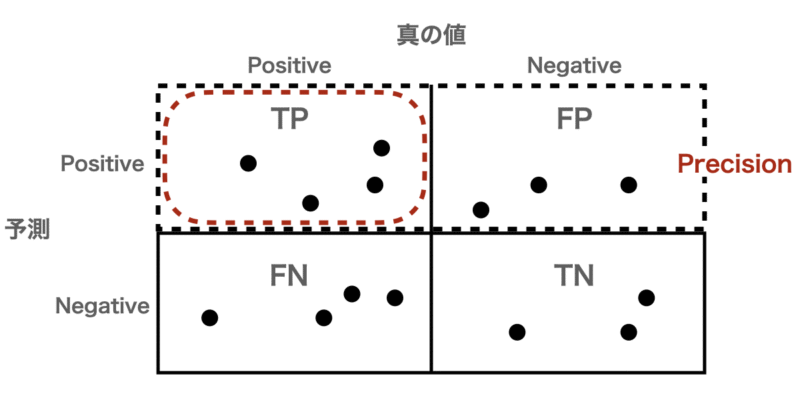
- 適合率(Precision):
予測で「陽性」と言ったもののうち、真の値も陽性だった割合
$$\text{Precision} = \frac{TP}{TP + FP}$$
例として、下の図からPrecisionは
$$\text{Precision} = \frac{4}{4 + 3} = 0.57$$
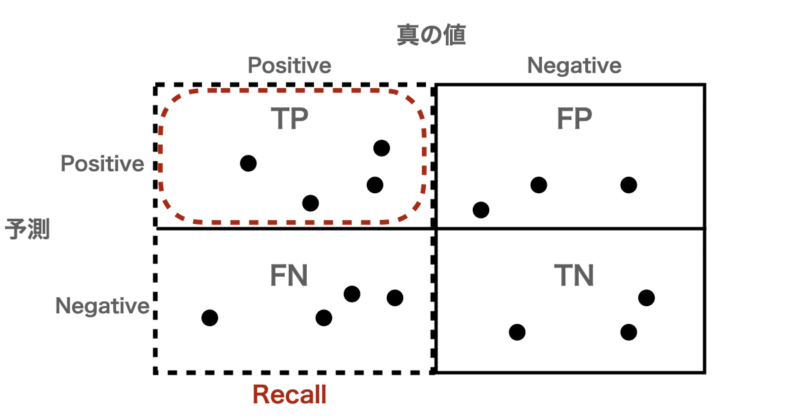
- 再現率(Recall):
真の値が陽性だったもののうち、正しく陽性と予測できた割合
$$\text{Recall} = \frac{TP}{TP + FN}$$
例として、下の図からRecallは
$$\text{Recall} = \frac{4}{4 + 4} = 0.5$$
◼️ 特徴・使いどころ
Precision(精度)は誤検出(FP)をどれだけ防げているかを評価するため、スパム判定やセキュリティアラートの誤報など誤検出を避けたい場合に使用します。
Recall(再現率)は 陽性(TP)をどれだけ取りこぼさなかったかを評価するため、病気の診断や異常検知など要請を見逃したくない場合に使用します。
◼️ 注意点
Precision を上げようとすると Recall が下がりやすく、その逆も同様です(トレードオフの関係)。
両者のバランスを取るために、次の F1 Score がよく用いられます。
F1 Scoreと F$\beta$ Score
- F1 Score:
Precision と Recall の調和平均で、バランスを重視した評価指標です。
$$F_1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$$
- Fβ Score
Recall を重視する度合いを $\beta$ で調整できます。
$$F_\beta = (1 + \beta^2) \times \frac{\text{Precision} \times \text{Recall}}{(\beta^2 \times \text{Precision}) + \text{Recall}}$$
◼️ 特徴・使いどころ
$F_1$ ScoreはRcallとPrecisionの全体バランスを見たいときに使用します。一方でRecall を重視したい場合は$F_\beta$ Scoreで$\beta$ > 1、Precisionを重視したい場合は$\beta$ > 1にて設定して計算します。
◼️ 注意点
分子にTPのみしか含まれないため、正例と負例を対象に扱っていません。そのため、予測値と真の値について正例と負例を入れ替えるとスコアが変化することがあります。
対数損失(Log Loss)
- 対数損失(Logloss):
モデルの「確率的な予測の信頼性」を評価します。
予測確率 $p_i$ が正解ラベル $y_i \in \{0,1\}$ にどれだけ近いかを評価します。
$$\text{LogLoss} = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log(p_i) + (1 – y_i)\log(1 – p_i)]$$
| No | 正解ラベル ($y_i$) | 予測確率 ($p_i$) | $y_i \log(p_i) + (1 – y_i)\log(1 – p_i)$ |
|---|---|---|---|
| 1 | 1 | 0.95 | 0.0513 |
| 2 | 1 | 0.60 | 0.5108 |
| 3 | 0 | 0.10 | 0.1053 |
| 4 | 1 | 0.05 | 2.9957 |
| 5 | 0 | 0.90 | 2.3026 |
| 合計 | — | — | 5.9657 |
| LogLoss(平均) | — | — | 1.1931 |
◼️ 特徴・使いどころ
予測確率が正解に近いほどスコアは小さく(良く)なり、自信を持って間違えた場合(例:p=0.99で外した)は大きく減点されます。確率出力を持つモデル(ロジスティック回帰、LightGBM、XGBoostなど)に使用することができます。
多クラス分類(Multi-class Classification)
次に、3クラス以上の分類問題(例:画像分類)における評価指標について説明します。
Multi-class Accuracy
- Multi-class Accuracy:
二値分類問題におけるAccuracyを多クラス問題へと拡張した指標。予測した内の正答率を表します。
$$\text{Accuracy} = \frac{\text{Number of correct predictions}}{\text{Total predictions}}$$
◼️ 特徴・使いどころ
クラス間に偏りがなければ単純でわかりやすい指標であり、分類の正答率を重視したい場合に使用します。また、分類問題であればどの学習モデルでも適用可能です。
◼️ 注意点
二値分類問題と同様にクラスごとのサンプル数に偏りがあると正しく評価できない場合があります。例えば、あるクラスが学習データの90%を占める場合、常にそのクラスを予測するだけでAccuracy=0.9となってしまうからです。そのため、後述のF1スコア(Macro/Micro/Mean)を使うと、より公平に評価可能です。
Multi-class LogLoss
- Multi-class LogLoss:
二値分類問題のLogLossを多クラス分類に拡張した指標であり、各分類の予測確率に対して対数をとって符号を反転させて計算しています。
$$\text{LogLoss} = -\frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{C} y_{i,c} \log(p_{i,c})$$
$N$:サンプル数
$C$:クラス数
$y_{i,c}$:1(正解クラス)または0(それ以外)
$p_{i,c}$:クラス $c$ に属する確率
| No. | 正解クラス $y_i$ | 予測確率 $p_{i,0}$ | $p_{i,1}$ | $p_{i,2}$ | 計算式 |
|---|---|---|---|---|---|
| 1 | 0 | 0.80 | 0.15 | 0.05 | $-\log(0.80) = 0.2231 $ |
| 2 | 1 | 0.10 | 0.70 | 0.20 | $-\log(0.70) = 0.3567$ |
| 3 | 2 | 0.05 | 0.15 | 0.80 | $-\log(0.80) = 0.2231$ |
| 4 | 1 | 0.20 | 0.60 | 0.20 | $-\log(0.60) = 0.5108$ |
| 5 | 2 | 0.90 | 0.05 | 0.05 | $-\log(0.05) = 2.9957$ |
| 合計 | — | — | — | — | 4.3089 |
| LogLoss(平均) | — | — | — | — | 0.8618 |
◼️ 特徴・使いどころ
二値分類問題とほとんど同様ですが、予測確率が正解に近いほどスコアは小さく(良く)なり、自信を持って間違えた場合(例:p=0.99で外した)は大きく減点されます。確率出力を持つモデル(ロジスティック回帰、LightGBM、XGBoostなど)に使用することができます。
Macro F1/ Micro F1 / Mean F1
以下のテーブルに示すような実際の分類 {0,1,2} に対して予測を行った場合のMacro F1/ Micro F1 / Mean F1を解説していきます。
| No | 実際のラベル $y_i$ | 予測ラベル $\hat{y}_i$ | 備考 |
|---|---|---|---|
| 1 | 0 | 0 | 正解 |
| 2 | 1 | 2 | 不正解 |
| 3 | 2 | 2 | 正解 |
| 4 | 1 | 1, 2 | 部分的に正解 |
| 5 | 0, 2 | 0, 1 | 部分的に正解 |
- Macro F1:
クラスごとにF1を計算して平均を取った指標。クラス数に偏りがあっても、全クラスを平等に評価します。
$$\text{Macro F1} = \frac{1}{C} \sum_{c=1}^{C} F1_c$$
最初の例に対して上記式で計算すると以下の表のとおりになります。
| クラス | TP | FP | FN | Precision | Recall | F1 |
|---|---|---|---|---|---|---|
| 0 | 2 | 0 | 0 | $\frac{2}{2+0} = 1.00$ | $\frac{2}{2+0} = 1.00$ | 1.00 |
| 1 | 1 | 1 | 1 | $\frac{1}{1+1} = 0.50$ | $\frac{1}{1+1} = 0.50$ | 0.50 |
| 2 | 1 | 2 | 1 | $\frac{1}{1+2} = 0.33$ | $\frac{1}{1+1} = 0.50$ | 0.40 |
| Macro F1(平均) | — | — | — | — | — | 0.63 |
- Micro F1:
全クラスでTP, FP, FNを合算して1つのF1を求めており、サンプル数が多いクラスを重視する指標になります。
$$\text{Micro F1} = \frac{2 \times \sum_{c=1}^{C} TP_c}{2 \times \sum_{c=1}^{C} TP_c + \sum_{c=1}^{C} FP_c + \sum_{c=1}^{C} FN_c}$$
最初の例に対して上記式で計算すると以下表のとおりになります。
| 集計項目 | 値 |
|---|---|
| $TP_{total}$ | 4 |
| $FP_{total}$ | 3 |
| $FN_{total}$ | 2 |
| $F1_{micro}$ | $ \frac{2 \times 4}{2 \times 4 + 3 + 4} = 0.615 $ |
- Mean F1:
各レコードごとに F1スコアを計算し平均した指標になります。レコード単位で平均性能を確認したい場合に有用な指標です。
$$\text{Mean F1} = \frac{1}{N} \sum_{i=1}^{N} F1_i$$
最初の例に対して上記式で計算すると以下表のとおりになります。
| No | 実際のラベル $y_i$ | 予測ラベル $\hat{y}_i$ | TP | FP | FN | Precision | Recall | F1 |
|---|---|---|---|---|---|---|---|---|
| 1 | {0} | {0} | 1 | 0 | 0 | 1.00 | 1.00 | 1.00 |
| 2 | {1} | {2} | 0 | 1 | 1 | 0.00 | 0.00 | 0.00 |
| 3 | {2} | {2} | 1 | 0 | 0 | 1.00 | 1.00 | 1.00 |
| 4 | {1} | {1,2} | 1 | 1 | 0 | 0.50 | 1.00 | 0.67 |
| 5 | {0,2} | {0,1} | 1 | 1 | 1 | 0.50 | 0.50 | 0.50 |
| Mean F1 | — | — | — | — | — | — | — | 0.63 |
◼️ 特徴・使いどころ
Macro F1は全てのクラスを平等に評価できるためクラスが不均衡なデータに向いています。また、Micro F1はサンプル数に比例して重み付を行うため全体精度を確認したい場合に使用します。Mean F1はレコード単位で平均性能を確認したい場合に有用な指標です。
Quadratic Weighted Kappa(QWK)
- Quadratic Weighted Kappa (QWK):
順序付き分類(ordinal classification)」に特化した指標。人間の採点やレーティングの一致度を評価する際に使われます。
$$\kappa = 1 – \frac{\sum_{i,j} w_{i,j} O_{i,j}}{\sum_{i,j} w_{i,j} E_{i,j}}$$
ここで:
$O_{i,j}$:実際の混同行列(観測分布)
$E_{i,j}$:期待される混同行列の要素
$w_{i,j} = \frac{(i-j)^2}{(C-1)^2}$:誤差の重み
例として、以下の5つのレコードに対してQWKを計算してみます。
| No | 実際のラベル | 予測ラベル |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 2 |
| 3 | 2 | 2 |
| 4 | 1 | 1 |
| 5 | 2 | 0 |
まず、観測行列 $O_{i,j}$ は以下表のとおりに計算されます。
| 実際\予測 | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 |
次に重み行列を計算していきます。計算式は次のとおりです。
$$w_{i,j} = \frac{(i – j)^2}{(C – 1)^2}$$
$C$:クラスの総数(例:クラスが0,1,2の3段階なら $C=3$)
上記式に従って計算すると以下表のようになります。
| 実際\予測 | 0 | 1 | 2 |
|---|---|---|---|
| 0 | $\frac{(0-0)^2}{4} = 0.00$ | $\frac{(0-1)^2}{4} = 0.25$ | $\frac{(0-2)^2}{4} = 1.00$ |
| 1 | $\frac{(1-0)^2}{4} = 0.25$ | $\frac{(1-1)^2}{4} = 0.00$ | $\frac{(1-2)^2}{4} = 0.25$ |
| 2 | $\frac{(2-0)^2}{4} = 1.00$ | $\frac{(2-1)^2}{4} = 0.25$ | $\frac{(2-2)^2}{4} = 0.00$ |
次に期待行列 $E_{i,j}$ を計算します。計算式は以下のとおりです。
$$E_{i,j} = \frac{n_i \times m_j}{N}$$
$n_i$:実際クラス $i$ のサンプル数
$m_j$:予測クラス $j$ のサンプル数
$N$:全サンプル数
上記式に従って期待行列を計算した結果が以下のとおりです。
| 実際\予測 | 0 | 1 | 2 |
|---|---|---|---|
| 0 | $\frac{(1×2)}{5} = 0.4$ | $\frac{(1×1)}{5} = 0.2$ | $\frac{(1×2)}{5} = 0.4$ |
| 1 | $\frac{(2×2)}{5} = 0.8$ | $\frac{(2×1)}{5} = 0.4$ | $\frac{(2×2)}{5} = 0.8$ |
| 2 | $\frac{(2×2)}{5} = 0.8$ | $\frac{(2×1)}{5} = 0.4$ | $\frac{(2×2)}{5} = 0.8$ |
以上の計算から観測値に基づく重み付き誤差を計算した結果が以下のとおりです。
| 実際\予測 | $w_{i,j}$ | $O_{i,j}$ | $w_{i,j}O_{i,j}$ |
|---|---|---|---|
| 0,0 | 0.00 | 1 | 0.00 |
| 0,1 | 0.25 | 0 | 0.00 |
| 0,2 | 1.00 | 0 | 0.00 |
| 1,0 | 0.25 | 0 | 0.00 |
| 1,1 | 0.00 | 1 | 0.00 |
| 1,2 | 0.25 | 1 | 0.25 |
| 2,0 | 1.00 | 1 | 1.00 |
| 2,1 | 0.25 | 0 | 0.00 |
| 2,2 | 0.00 | 1 | 0.00 |
| 合計 | — | — | 1.25 |
また、期待値に基づく重み付き誤差は以下表のとおりです。
| 実際\予測 | $w_{i,j}$ | $E_{i,j}$ | $w_{i,j}E_{i,j}$ |
|---|---|---|---|
| 0,0 | 0.00 | 0.4 | 0.00 |
| 0,1 | 0.25 | 0.2 | 0.05 |
| 0,2 | 1.00 | 0.4 | 0.40 |
| 1,0 | 0.25 | 0.8 | 0.20 |
| 1,1 | 0.00 | 0.4 | 0.00 |
| 1,2 | 0.25 | 0.8 | 0.20 |
| 2,0 | 1.00 | 0.8 | 0.80 |
| 2,1 | 0.25 | 0.4 | 0.10 |
| 2,2 | 0.00 | 0.8 | 0.00 |
| 合計 | — | — | 1.75 |
以上の計算から、
$$\kappa = 1 – \frac{\sum_{i,j} w_{i,j} O_{i,j}}{\sum_{i,j} w_{i,j} E_{i,j}} = 1 – \frac{1.25}{1.75} = 1 – 0.7143 = 0.286$$
◼️ 特徴・使いどころ
$\kappa = 1$は完全一致であることを表し、反対に$\kappa = 0$はランダム予測と同等であることを表します。また、順序が遠いほど重いペナルティが課され、例えばスコア1を5と間違えるなどあった場合は$\kappa$が小さくなってしまいます。使いどころとしては医療診断のステージ分類(0〜4段階など)や評価スコア(例:A〜E, 1〜5点)の一致度評価が挙げられます。
まとめ:どの指標を使うべきか?
以上が分類問題における評価指標の解説になります。まとめとして各評価指標の特徴と適したケースをしたの表にまとめています。本記事が少しでも皆様の助けになれば幸いです。
| 指標 | 対応タスク | 特徴 | 向いている場面・使い分け |
|---|---|---|---|
| Accuracy | 二値 | 全体の正解率を表す。シンプルで直感的。 | クラス分布が均等な場合の基本評価。例:画像分類、明確なクラス境界がある問題。 |
| Precision | 二値 | Positive と予測した中で、実際に正しい割合。誤検出を抑えたい。 | 誤検出を避けたいタスク(例:スパム検知、詐欺検出)。 |
| Recall | 二値 | 実際の Positive のうち、どれだけ検出できたか。見逃しを抑えたい。 | 見逃しを避けたいタスク(例:疾病検出、異常検知)。 |
| F1スコア | 二値 | Precision と Recall の調和平均。両者のバランスを評価。 | Precision・Recall の両方を重視したいとき(例:分類モデル全体性能の比較)。 |
| Fβスコア | 二値 | F1の一般形。β>1でRecall重視、β<1でPrecision重視。 | Recall重視=医療分野、Precision重視=監視・警告システム。 |
| LogLoss | 二値 | 予測確率の信頼度を評価。確信を持って間違えると大きなペナルティを与える。 | 確率出力モデル(ロジスティック回帰・GBoostなど)。予測確率も評価したいとき。 |
| Multi-class Accuracy | 多クラス | クラス数が3以上で「正解率」を算出。 | 各クラスが均等に分布している場合。例:画像識別タスク。 |
| Multi-class LogLoss | 多クラス | 各クラスの確率分布を考慮。自信を持って誤ると重い罰。 | 確率出力モデル(LightGBM, XGBoostなど)での評価。 |
| Macro F1 | 多クラス | 各クラスのF1を単純平均。クラス間を平等に扱う。 | クラス不均衡があるデータで、全クラスを平等に評価したい場合。 |
| Micro F1 | 多クラス | 全サンプルでまとめて評価。頻出クラスが支配的。 | 全体的な分類精度を重視する場合。 |
| Mean F1 | 多クラス | レコード単位で $F_1$ を計算 | レコード単位で平均性能を確認したい場合に有用 |
| QWK | 多クラス | 順序を考慮した一致度。誤差の大きい分類を強く罰する。 | 等級・スコア分類(例:医療グレード、教師評価など)。 |