こんにちは!ぼりたそです!
「機械学習モデルの性能評価ってどうやればいいの?」
そんな疑問を持っている方に向けて、この記事ではクロスバリデーション(交差検証)という評価手法についてわかりやすく解説します!
この記事は以下のポイントでまとめています。
- クロスバリデーションとは?
- クロスバリデーションの種類
- クロスバリデーションの実行
それでは詳細に解説していきいます。
クロスバリデーションとは?
クロスバリデーションとは、機械学習モデルの性能(特に汎化性能)を客観的に評価する手法あり、適切なハイパーパラメータの選択やモデルの改善に役立ちます。
以下にクロスバリデーションの基本的な考え方についてわかりやすく説明します。
一般的な手法では、データを「トレーニング用」と「テスト用」に一度だけ分割してモデルを評価します。
しかしこの方法では、分割の仕方によって結果が大きく変わる可能性があります。
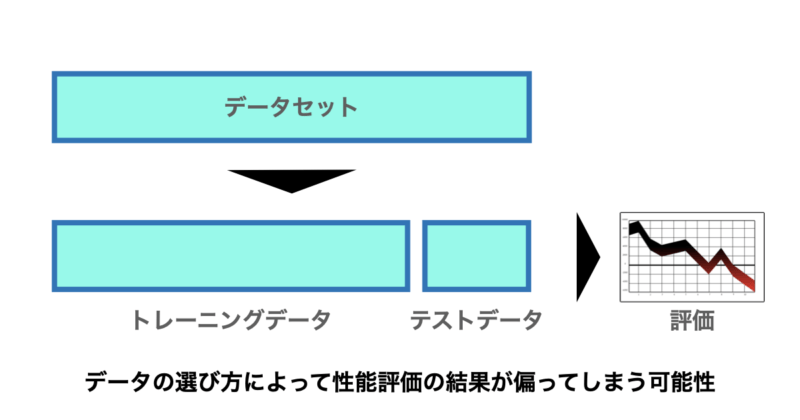
そこで活躍するのがクロスバリデーションです。データを複数のパターンに分割し直して評価を繰り返すことで、より安定した性能評価が可能となります。
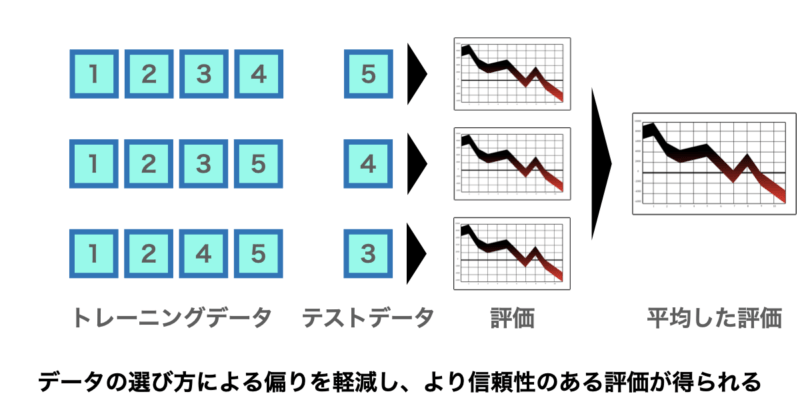
クロスバリデーションを用いることで以下のようなメリットが得られます。
■メリット
このようにクロスバリデーションはメリットも大きいですが、もちろんデメリットもあるのです。
以下が主なデメリットになります。
■デメリット
メリット、デメリットを理解して上で正しく使用したいですね。
クロスバリデーションの種類
クロスバリデーションについて何となく理解いただけたでしょうか?
次にクロスバリデーションの種類について説明していきたいと思います。
クロスバリデーションの種類としては主に以下の3つとなります。
以下の3つはデータセットの分割の方法が異なります。
- k分割交差検証 (k-Fold Cross-Validation)
- Leave-One-Out Cross-Validation (LOOCV)
- 層化k分割交差検証 (Stratified k-Fold Cross-Validation)
それでは順に説明していきます。
k分割交差検証 (k-Fold Cross-Validation)
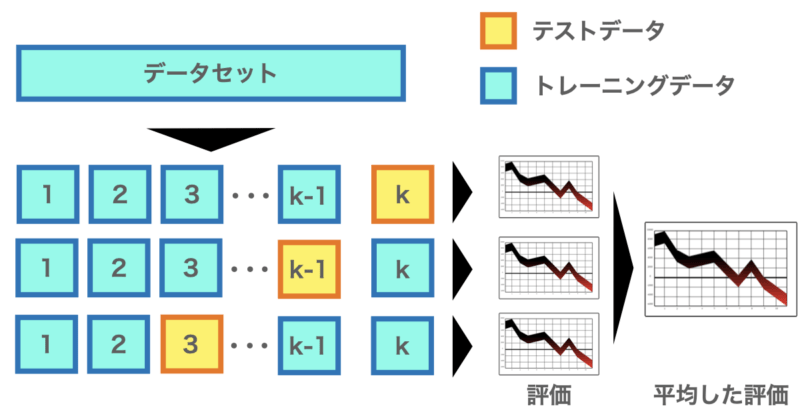
k-Fold Cross-Validationとは上の図のようにデータをk個のブロック(Fold)に均等に分け、それぞれを1回ずつテスト用として使い、残りでモデルを学習します。
これをk回繰り返し、平均スコアで性能を評価します。
この手法はクロスバリデーションの中でもよく使用される手法であり、過学習を避けつつデータを効率的に利用できるメリットがあります。
それでは実際にk-Fold Cross-Validationを実行してモデルの評価をしてみます。
まず以下の関数に従うデータを作成し、重回帰分析のモデルを構築します。その後、5 fold Cross-ValidationでMSE(平均二乗誤差)とR²(決定係数)を使用して予測性能を評価していきたいと思います。
$$y = 2x + 3x + 4x$$
import numpy as np
from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# サンプルデータ生成
np.random.seed(42)
X = np.random.rand(100, 3)
y = 2 * X[:, 0] + 3 * X[:, 1] + 4 * X[:, 2] + np.random.randn(100)
# 5分割クロスバリデーション設定
kf = KFold(n_splits=5, shuffle=True, random_state=42)
model = LinearRegression()
# 各Foldごとのスコアを保存するリスト
mse_list = []
r2_list = []
coeffs_per_fold = []
# クロスバリデーション実行
for fold, (train_idx, test_idx) in enumerate(kf.split(X), start=1):
X_train, X_test = X[train_idx], X[test_idx]
y_train, y_test = y[train_idx], y[test_idx]
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mse_list.append(mse)
r2_list.append(r2)
coeffs_per_fold.append(model.coef_)
print(f"Fold {fold}: MSE = {mse:.3f}, R^2 = {r2:.3f}, Coefficients = {model.coef_}")
# 平均スコア出力
average_mse = np.mean(mse_list)
average_r2 = np.mean(r2_list)
average_coeffs = np.mean(coeffs_per_fold, axis=0)
print("\n==== 平均評価指標 ====")
print(f"Average MSE = {average_mse:.3f}")
print(f"Average R^2 = {average_r2:.3f}")
print(f"Average Coefficients = {average_coeffs}")
出力結果は以下の通りです。
| Fold | MSE | R² | Coefficients |
|---|---|---|---|
| 1 | 2.017 | 0.573 | [2.11, 2.92, 4.69] |
| 2 | 0.622 | 0.838 | [2.20, 2.82, 4.54] |
| 3 | 0.681 | 0.819 | [2.39, 2.91, 4.44] |
| 4 | 0.444 | 0.810 | [2.30, 2.93, 4.61] |
| 5 | 1.477 | 0.504 | [2.46, 2.66, 4.62] |
| 平均 | 1.049 | 0.709 | [2.29, 2.85, 4.58] |
結果を見ると5 Fold Cross-Validationの平均としてMSE=1.05、R²= 0.709と良好なモデルになっています。
それぞれのFoldに注目するとMSEやR²がブレていることがわかります。クロスバリデーションせずに評価してしまうと予測性能を正しく評価できない可能性があるということですね。
また、今回変数を3つ設定しており、それぞれの係数がそれぞれ [2, 3, 4] となるように設定していました。最終的に出力された計数を見ると、[2.29 2.85 4.58] となっており、そこそこあっています。
以上がpythonを使用したk Fold Cross-Validationの実行となります。
Leave-One-Out Cross-Validation (LOOCV)
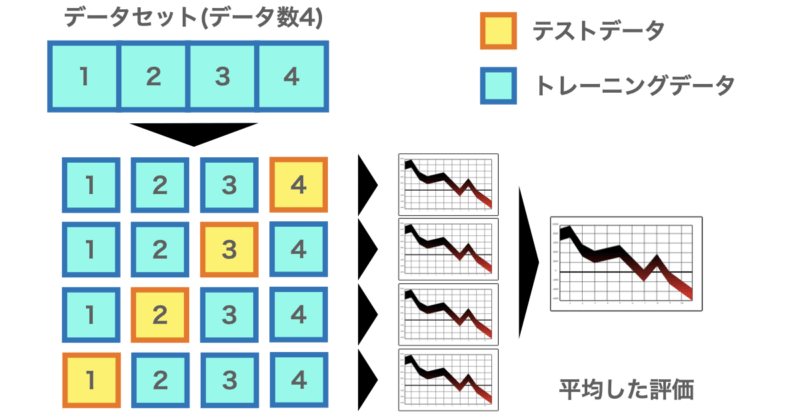
LOOCVはデータを1件だけテスト用にし、残りすべてを学習データとします。
これを全データに対して繰り返し、平均スコアで性能を評価します。
この手法のメリットとしてはデータ数が少ない場合でもモデルを評価できる点が挙げられます。逆にデータ数が多い場合(データが30以上)の場合は計算コストが大きくなってしまう可能性があります。
LOOCVについても実際にPythonを使用して擬似的な関数を作成し、評価していきましょう。
先ほどと同様に以下の関数に従うデータを作成し、重回帰分析のモデルを構築します。その後、LOOCVでMSE(平均二乗誤差)、 R²(決定係数)を使用して予測性能を評価していきたいと思います。
$$y = 2x + 3x + 4x$$
import numpy as np
from sklearn.model_selection import LeaveOneOut
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# データ生成
np.random.seed(42)
X = np.random.rand(100, 3)
y = 2 * X[:, 0] + 3 * X[:, 1] + 4 * X[:, 2] + np.random.randn(100)
# モデルとLOOCVの設定
model = LinearRegression()
loo = LeaveOneOut()
# 予測結果と係数の格納用
y_pred = np.zeros_like(y)
coefs = np.zeros((len(y), X.shape[1])) # 100 × 3
# LOOCVの実行
for i, (train_idx, test_idx) in enumerate(loo.split(X)):
X_train, X_test = X[train_idx], X[test_idx]
y_train = y[train_idx]
model.fit(X_train, y_train)
y_pred[test_idx] = model.predict(X_test)
coefs[i] = model.coef_
# MSEとR²の計算
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
# 係数の平均計算
mean_coefs = np.mean(coefs, axis=0)
# 結果の出力
print(f"LOOCV - MSE: {mse:.3f}")
print(f"LOOCV - R²: {r2:.3f}")
print(f"LOOCV - 平均係数: {mean_coefs}")データが100個あるため各Foldの結果は出力していませんが、最終的な平均値を見ると、MSEは0.996、R²は0.731と良好なモデルとなっています。
変数の係数についても[2.278, 2.842, 4.570]と実際の[2, 3, 4]と比較すると大体あっていますね。
以上がLOOCVについての説明とPythonによる評価結果になります。
層化k分割交差検証 (Stratified k-Fold Cross-Validation)
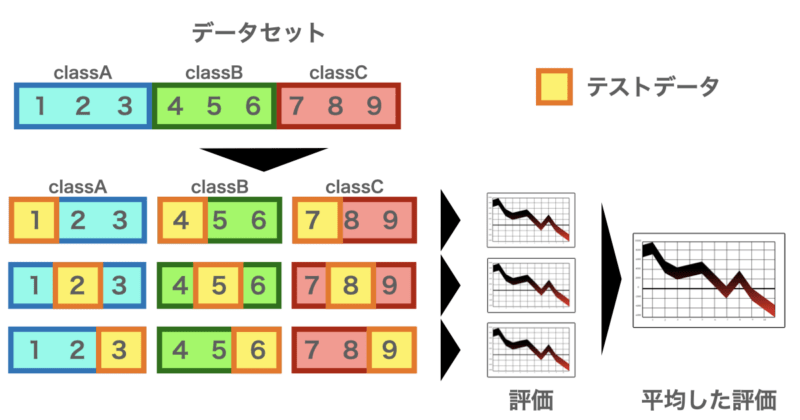
Stratified k-Fold Cross-Validation(層化k分割交差検証)は、クラス分類問題において特に効果的な交差検証手法です。
通常のk-Fold Cross-Validationでは、データをランダムにk個のFoldに分割しますが、分類問題でクラスの数に偏り(クラス不均衡)がある場合、Foldごとにクラスの分布が大きく異なってしまう可能性があります。
たとえば、全体で「陽性:陰性 = 9:1」のような偏ったデータの場合、あるFoldではほとんどが陽性、別のFoldでは陰性が全く含まれない、といった状況が起こることがあります。これではモデルの性能を正確に評価することができません。
Stratified k-Foldでは、各Fold内でもクラスの比率が元のデータセットとできるだけ近くなるように分割されます。これにより、各Foldでの学習・評価がバランスよく行われ、より安定したモデル評価が可能になります。
Stratified k-Fold Cross-Validationについても実際に使用していきましょう。
ここでは、Pythonで作成した2クラス分類問題(説明変数20個)を使って、Stratified 5-Fold Cross-Validationを実行し、ロジスティック回帰モデルの性能を正答率(Accuracy)で評価してみます。
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import StratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 仮想のデータ生成
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
# 層化k分割交差検証を設定
num_folds = 5
skf = StratifiedKFold(n_splits=num_folds, shuffle=True, random_state=42)
# ロジスティック回帰モデルを設定
model = LogisticRegression()
# 各フォールドでの性能評価を実行
fold_accuracy_scores = []
for fold, (train_index, test_index) in enumerate(skf.split(X, y), start=1):
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
fold_accuracy_scores.append(accuracy)
print(f"Fold {fold}: Accuracy = {accuracy}")
# 平均精度を計算して表示
average_accuracy = np.mean(fold_accuracy_scores)
print(f"Average Accuracy across {num_folds} folds = {average_accuracy}")
'''
Fold 1: Accuracy = 0.87
Fold 2: Accuracy = 0.885
Fold 3: Accuracy = 0.87
Fold 4: Accuracy = 0.86
Fold 5: Accuracy = 0.86
Average Accuracy across 5 folds = 0.869
'''
出力結果は以下の通りです。
| Fold | Accuracy |
|---|---|
| 1 | 0.870 |
| 2 | 0.885 |
| 3 | 0.870 |
| 4 | 0.860 |
| 5 | 0.860 |
| 平均 | 0.869 |
出力結果を見ると平均正答率は0.869と良好なモデルが構築できているのが分かります。
それぞれのFlodにおける正答率に注目すると、基本的には0.86-0.88程度であり、ブレの少なく安定したモデルといえます。
以上がStratified k-Fold Cross-Validationの説明と実際の評価結果になります。
終わりに
以上がクロスバリデーションについての解説になります。構築したモデルの性能評価をする際にはよく使用する方法ですので、使いこなしたいですね。また、クロスバリデーションと言っても様々な手法があるので、場合によって使い分けられるようにしていきたいですね。


コメント
[…] ぼりたそブログ「クロスバリデーション(交差検証)についてわかりやすく解説」 […]