特徴量エンジニアリング～モデル性能を引き出す特徴量の工夫～

こんにちは、ぼりたそです！

前回の記事では「データ前処理の基礎」として、欠損値処理やスケーリングについて紹介しました。前処理をすることでデータは「学習可能な状態」に整いますが、それだけでは十分ではありません。

合わせて読みたい

機械学習の性能をさらに引き出すためには、モデルがより学びやすい形にデータを工夫することが重要です。この工夫こそが 特徴量エンジニアリング（Feature Engineering） です。

この記事では以下のポイントで特徴量エンジニアリングの各手法やそのメリット&デメリットを解説していきます。

Point

特徴量エンジニアリングとは？
　
特徴量変換
　
特徴量選択
　
特徴量生成
　
次元削減

特徴量エンジニアリングとは？
特徴量変換 ― データの形を整える
特徴量選択 ― ノイズを取り除く
新しい特徴量の生成 ― モデルの表現力を広げる
次元削減 ― 特徴量をまとめて効率化
まとめ

特徴量エンジニアリングとは？

特徴量エンジニアリングとは、既存のデータを加工したり、新しい特徴を生成して、モデルの性能を高める作業のことです。
前処理が「データを学習可能に整える」段階なら、特徴量エンジニアリングは「より良く学習できる形に改善する」段階です。

例えば、収入に対して対数変換を行えば外れ値の影響を抑えられますし、身長と体重からBMIを作れば健康状態を示す新しい指標を追加できます。こうした工夫がモデルの予測精度を大きく左右します。

特徴量変換 ― データの形を整える

特徴量変換とは、既存の数値データに数学的な変換を加えて分布を扱いやすくする方法です。代表的な手法は次の通りです。

対数変換（log変換）：数値のスケールが極端に大きな値の影響を抑える
平方根変換：外れ値が中程度のとき有効
Box-Cox変換／Yeo-Johnson変換：データを正規分布に近づける
標準化・正規化：分布や範囲を揃える（前処理編で詳述）

これらを使うことで、線形モデルでも非線形関係をうまく学習できることがあります。

また、上記の特徴量変換を行うことによるメリット&デメリットは以下のとおりです。

メリット
- 外れ値の影響を抑えられる
- 線形モデルでも非線形関係を捉えやすくなる
デメリット
- 不適切な変換は情報を失う可能性がある
- 元の意味が直感的に分かりにくくなる

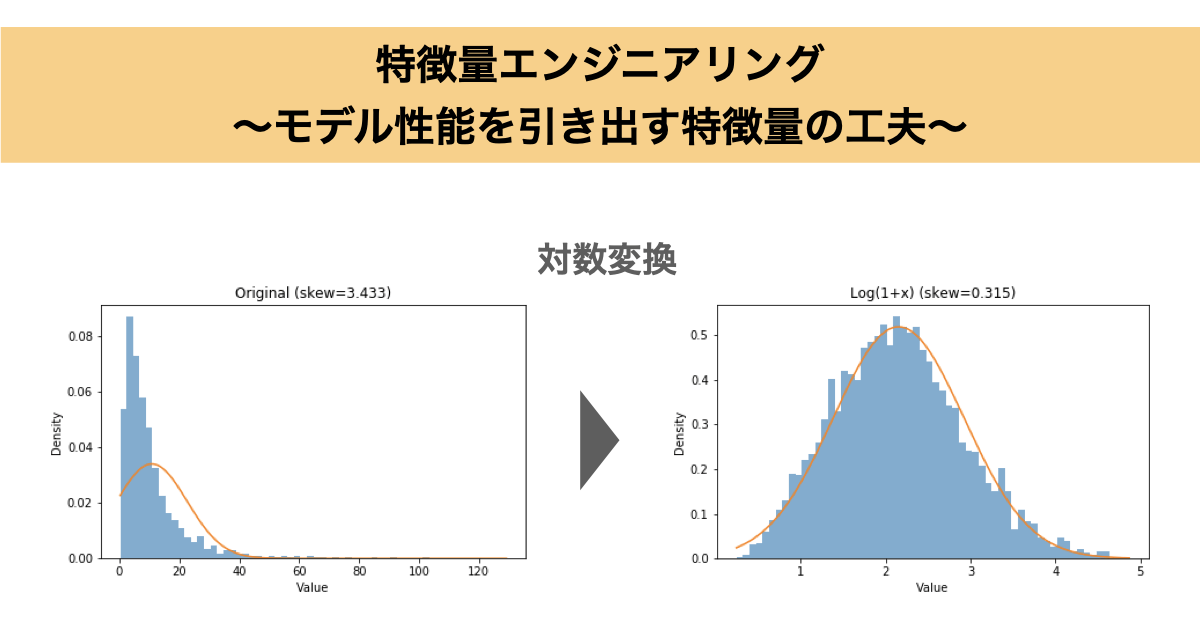
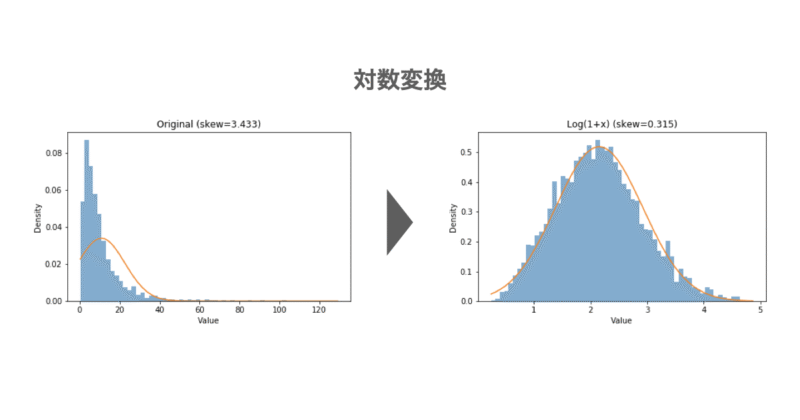
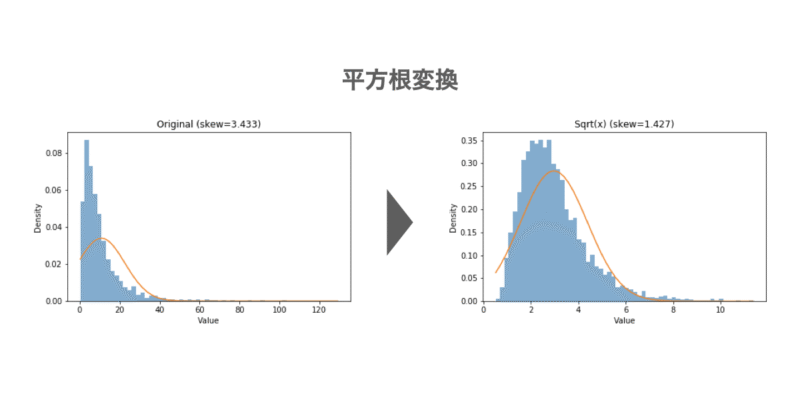
以下に歪んだ分布に対する対数変換および平方根変換を実行したPythonコードを示します。図の通り、変換後は分布が正規分布に近づいており、特に対数変換は効果が大きいことがわかります。

例：歪んだ分布のlog変換、平方根変換

# ヒストグラムで「元の分布 → 対数変換 → 平方根変換」の変化を可視化
# - seabornは不使用（matplotlibのみ）
# - 各図は独立プロット

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 1) 右に裾が長い分布を用意（例：対数正規分布）
rng = np.random.default_rng(42)
data = rng.lognormal(mean=2.0, sigma=0.9, size=3000)  # 強めの右裾
# ★自分のデータを使うなら： data = your_numpy_array_or_series

# 2) 変換
data_log = np.log1p(data)   # 0にも安全 log(1+x)
data_sqrt = np.sqrt(data)   # 穏やかに圧縮

# 3) 指標（平均・標準偏差・歪度）を比較表示
stats = pd.DataFrame({
    "mean": [np.mean(data), np.mean(data_log), np.mean(data_sqrt)],
    "std":  [np.std(data, ddof=0), np.std(data_log, ddof=0), np.std(data_sqrt, ddof=0)],
    "skew": [pd.Series(data).skew(), pd.Series(data_log).skew(), pd.Series(data_sqrt).skew()],
}, index=["Original", "Log(1+x)", "Sqrt(x)"])

print("=== 分布の指標（平均・標準偏差・歪度） ===")
print(stats.round(4))

# 4) 正規分布（平均・標準偏差に合わせたガウス分布）を重ねて表示する関数
def plot_hist_with_gaussian(x, title, bins=60):
    mu = np.mean(x)
    sigma = np.std(x, ddof=0)
    xs = np.linspace(np.min(x), np.max(x), 400)
    pdf = (1.0/(sigma*np.sqrt(2.0*np.pi))) * np.exp(-0.5*((xs-mu)/sigma)**2)

    plt.figure()
    plt.hist(x, bins=bins, density=True, alpha=0.6)  # density=True でPDFと比較しやすい
    plt.plot(xs, pdf)  # カラー指定なし（デフォルト）
    plt.title(title)
    plt.xlabel("Value")
    plt.ylabel("Density")
    plt.tight_layout()
    plt.show()

# 5) 可視化（ヒストグラム3枚）
plot_hist_with_gaussian(
    data,
    f"Original (skew={stats.loc['Original','skew']:.3f})",
    bins=60
)
plot_hist_with_gaussian(
    data_log,
    f"Log(1+x) (skew={stats.loc['Log(1+x)','skew']:.3f})",
    bins=60
)
plot_hist_with_gaussian(
    data_sqrt,
    f"Sqrt(x) (skew={stats.loc['Sqrt(x)','skew']:.3f})",
    bins=60
)

特徴量選択 ― ノイズを取り除く

特徴量選択は「どの特徴量を残すか」を決める作業です。すべての特徴量が予測に有効とは限りません。相関の高い特徴量が複数ある場合や、ほとんど変動しない特徴量がある場合、それらを削除することでモデルをシンプルにできます。

代表的な手法は以下のとおりです。

特徴量同士の相関：高い相関を持つ特徴量を削除
特徴量の分散：ほとんど変動しない特徴量を削除
モデルによる重要度：ランダムフォレストや勾配ブースティングで重みを確認
逐次選択：モデル性能を見ながら特徴を追加・削除

また、上記の特徴量選択を行うことによるメリット&デメリットは次のとおりです。

メリット
- 過学習の防止
- 学習速度の向上
- モデルの解釈性が増す
デメリット
- 有用な特徴を削除してしまうリスク
- 単純な基準では重要な特徴を見逃すことがある

以下に相関の高い特徴量を確認するためのPythonコードを記載します。これにより機械学習モデルのノイズになりそうな特徴量をあらかじめ削除します。

例：相関の高い特徴量を確認

df = pd.DataFrame({
    "age":[20, 30, 40, 50],
    "income":[200, 400, 800, 1600],
    "spending":[220, 390, 810, 1550]
})

corr = df.corr()
print("=== 相関行列 ===")
print(corr)

新しい特徴量の生成 ― モデルの表現力を広げる

新しい特徴量を作ることで、モデルが学習できるパターンを増やせます。単純な列同士の比率や積み合わせだけでも、意味のある指標になることがあります。ドメイン知識を活かせる場面でも大きな力を発揮します。

代表的な手法：

比率や差分の作成：例：売上／顧客数、変化率など
統計量の追加：平均・中央値・最大値など
多項式特徴量（PolynomialFeatures）：2次や3次の組み合わせを自動生成
ドメイン知識による特徴量：化学なら分子記述子、健康ならBMIなど

また、上記のような特徴量生成を用いることによるメリット&デメリットについては次のとおりです。

メリット
- モデルの表現力を補える
- ドメイン知識を活かせる
デメリット
- 作業に時間がかかる
- 無意味な特徴を作るとノイズや過学習につながる

以下に身長、体重の特徴量から新しい特徴量としてBMIを生成するPythonコードを示します。これによりモデルの表現力を広げられる可能性があります。

例：身長、体重からBMIの生成

df = pd.DataFrame({
    "weight":[60, 70, 80],
    "height":[1.65, 1.70, 1.75]
})

df["BMI"] = df["weight"] / (df["height"]**2)
print(df)

次元削減 ― 特徴量をまとめて効率化

特徴量が多すぎると計算コストが増えたり、過学習のリスクが高まります。そのようなときに使えるのが 次元削減 です。

代表的な手法：

主成分分析（PCA）：分散が大きい方向を抽出して圧縮
線形判別分析（LDA）：クラスをよく分ける方向を抽出
t-SNE・UMAP：可視化に特化した次元削減

また、上記の次元削減を使用することによるメリット&デメリットは次のとおりです。

メリット
- 特徴量を圧縮して計算効率を改善
- ノイズを削減できる
- 可視化に便利
デメリット
- 特徴量の解釈が難しくなる
- 有益な情報も一緒に削ってしまうリスク

次元削減については以下の記事にまとめてありますので、興味のある方は参照いただけますと幸いです。

合わせて読みたい

以下に簡単な例として3次元の特徴量をPCAにより2次元に圧縮するPythonコードを示します。

例：PCAで3列を2次元に圧縮

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

df = pd.DataFrame({
    "weight":[60, 70, 80, 90],
    "height":[1.65, 1.70, 1.75, 1.80],
    "age":[25, 35, 45, 55]
})

X_std = StandardScaler().fit_transform(df)

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)
print(X_pca)