こんにちは!ぼりたそです!
今回はガウス過程回帰で登場する「カーネル関数」について初心者の方にもわかりやすく説明していきたいと思います。
ざっくりとした説明ですので、あまり身構えずにご覧になっていただければと思います。
この記事は以下のポイントでまとめています。
- カーネル関数とは
- カーネル関数の種類と特徴
- Pythonによる計算の実行
- オススメの書籍
それでは詳しく説明していきます。
カーネル関数とは
それでは早速カーネル関数とは何なのか?について説明していきます。
ガウス過程回帰(GPR)やサポートベクターマシン(SVM)などで登場するカーネル関数とはデータ間がどれだけ似ているかを評価する指標です。
もう少しわかりやすく例を使って説明していきます。

例えば上のように丸、三角、四角の図形が並んでいたとします。
この図形の中で似たもの同士をまとめていくつかのグループに分けてくださいと言われたら、あなたはどのようにグルーピングするでしょうか?
恐らく、多くの方は下の2パターンの分け方をするのではないでしょうか?
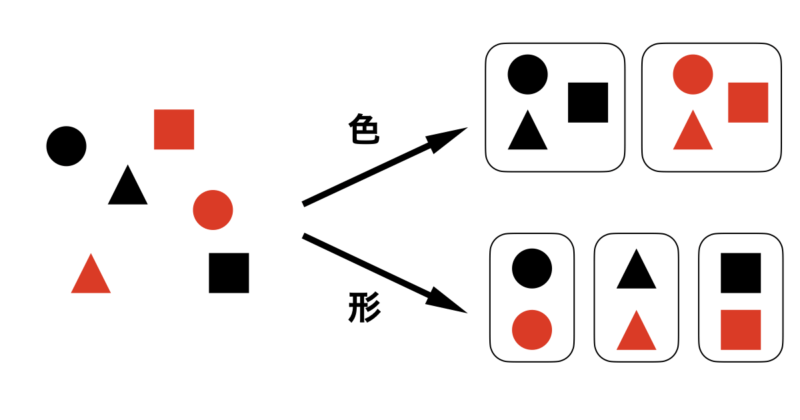
一つは色が同じであるグループとして黒と赤の図形で分けるパターン
二つ目は形が同じであるグループとして丸、三角、四角で分けるパターン
どちらも妥当なグルーピングですよね。違うのは「色」か「形」どちらの指標を使ったかと言うことだけです。
この色や形が“似ているかどうか”を数値で表すのが“カーネル関数”です。カーネル関数は、どのような基準で『似ている』と判断するかを数式で定義します。
ガウス過程回帰を実行する際にもデータ間の類似度を評価するためにカーネル関数を使用しますが、どの指標で似ていると判断するかはカーネル関数によって異なります。
例えば、データ間のユークリッド距離の近さで判断するカーネル関数もあれば、周期性や内積の大きさで判断するカーネル関数もあります。
カーネル関数の種類と特徴
カーネル関数についてはなんとなく理解いただけたのではないでしょうか?
ここからはカーネル関数の種類とその特徴について説明していきます。
今回は広く知られているカーネルとして以下の6つを紹介します。
- ガウスカーネル(RBF kernel)
- Matern カーネル(Matern kernel)
- 周期カーネル(Periodic kernel)
- 線形カーネル(Linear kernel)
- 多項式カーネル(Polynomial kernel)
- 指数カーネル(Exponential kernel)
ガウシアンカーネル(RBF kernel)
$$k(x, x’) = \exp\left(-\frac{|x – x’|^2}{2\sigma^2}\right) $$
ガウスカーネル(RBFカーネル)は、上記の数式で定義されるカーネル関数で、データ同士の距離が近いほど「類似している」と評価する仕組みです。
この関数は、非線形なデータの関係も捉えることができ、なめらかな関数の形状を予測するのに適しています。
幅広いデータに使用することができる汎用型のカーネル関数で最も使用されるカーネル関数の一つと言えます。
ハイパーパラメータは $\sigma$ であり、データ間の類似性を評価する際に、どれだけ遠いデータを類似とみなすかを調整します。
- $\sigma$ が大きい → 広い範囲のデータを類似とみなす
- $\sigma$ が小さい → 近いデータのみを類似とみなす
ガウシアンカーネルを使用するメリット、デメリットは以下の通りです。
メリット
デメリット
実際にPythonにより二次元座標間についてガウシアンカーネルで計算してみましょう。
今回、(0, 0), (1, 1), (2, 2), (3, 3)の四つの座標についてガウシアンカーネルを計算しました。ハイパーパラメータ $\sigma$ は1.0で設定しています。
計算結果は以下のように4×4のマトリクスでカーネルの共分散行列が出力されます。
$$K = \begin{bmatrix}
k((0,0), (0,0)) & k((0,0), (1,1)) & k((0,0), (2,2)) & k((0,0), (3,3)) \\
k((1,1), (0,0)) & k((1,1), (1,1)) & k((1,1), (2,2)) & k((1,1), (3,3)) \\
k((2,2), (0,0)) & k((2,2), (1,1)) & k((2,2), (2,2)) & k((2,2), (3,3)) \\
k((3,3), (0,0)) & k((3,3), (1,1)) & k((3,3), (2,2)) & k((3,3), (3,3))
\end{bmatrix}
$$
使用するコードは以下の通りです。
import numpy as np
from sklearn.metrics.pairwise import rbf_kernel
# 二次元座標の例
coords = np.array([[0, 0], [1, 1], [2, 2], [3, 3]])
# ガウシアンカーネルのパラメータ(例)
gamma = 1.0
# ガウシアンカーネルを計算する関数
def gaussian_kernel(coord1, coord2):
return np.exp(-gamma * np.linalg.norm(coord1 - coord2) ** 2)
# ガウシアンカーネルを計算
gaussian_kernel_matrix = rbf_kernel(coords, gamma=gamma)
# 計算結果を出力
print("\nGaussian Kernel Matrix:")
print(gaussian_kernel_matrix)計算結果は以下の通りです。
$$K = \begin{bmatrix}
1.00 & 0.14 & 0.00 & 0.00 \\
0.14 & 1.00 & 0.14 & 0.00 \\
0.00 & 0.14 & 1.00 & 0.14 \\
0.00 & 0.00 & 0.14 & 1.00
\end{bmatrix}
$$
この行列から、座標が近いと値が大きく、遠いと急激に小さくなることが分かります。RBFカーネルは非常に滑らかな関数を仮定するため、非類似なデータ(距離が遠い)にはほとんど影響を与えないことが特徴です。
Matern カーネル(Matern kernel)
$$k(x, x’) = \frac{2^{1-\nu}}{\Gamma(\nu)} \left(\frac{\sqrt{2\nu}|x – x’|}{\rho}\right)^\nu K_\nu\left(\frac{\sqrt{2\nu}|x – x’|}{\rho}\right)$$
Maternカーネルは、ガウシアンカーネル(RBFカーネル)に似ていますが、「どの程度なめらかな関数を作るか」を細かく調整できるのが特徴です。
特に、滑らかさを制御するパラメータ $\nu$ を持っており、この値を変えることで以下のような振る舞いになります:
- $\nu$ が小さい → ギザギザした関数(非連続な見た目)
- $\nu$ が大きい → 滑らかな関数(RBFに近づく)
また、$\rho$ は距離のスケール(どれくらい離れた点を「似ている」とみなすか)を調整するパラメータで、RBFカーネルの $\sigma$ と似た役割を持ちます。
$\nu=\infty$ の極限では、Maternカーネルはガウシアンカーネルと同じ形になります。このため、「ガウシアンカーネルの一般化」と呼ばれることがあります。
Maternカーネルを使用するメリットとデメリットは以下の通りです。
メリット
デメリット
MaternカーネルについてもPythonにて二次元座標間の計算を実行してみました。
同様に(0, 0), (1, 1), (2, 2), (3, 3)の四つの座標についてMaternカーネルを計算しました。ハイパーパラメータである $\nu$ と $\rho$ はそれぞれ1.5, 1.0にて設定しています。
計算結果は以下のように4×4のマトリクスでカーネルの共分散行列が出力されます。
$$K = \begin{bmatrix}
k((0,0), (0,0)) & k((0,0), (1,1)) & k((0,0), (2,2)) & k((0,0), (3,3)) \\
k((1,1), (0,0)) & k((1,1), (1,1)) & k((1,1), (2,2)) & k((1,1), (3,3)) \\
k((2,2), (0,0)) & k((2,2), (1,1)) & k((2,2), (2,2)) & k((2,2), (3,3)) \\
k((3,3), (0,0)) & k((3,3), (1,1)) & k((3,3), (2,2)) & k((3,3), (3,3))
\end{bmatrix}
$$
実行したコードは以下の通りです。
import numpy as np
from sklearn.metrics.pairwise import pairwise_kernels
# 二次元座標の例
coords = np.array([[0, 0], [1, 1], [2, 2], [3, 3]])
# Matérnカーネルのパラメータ(νは平滑化パラメータ)
nu = 1.5
length_scale = 1.0
# Matérnカーネルを計算する関数
def matern_kernel(coord1, coord2):
distance = np.linalg.norm(coord1 - coord2)
sqrt_3_nu_distance = np.sqrt(3 * nu) * distance / length_scale
return (1. + sqrt_3_nu_distance) * np.exp(-sqrt_3_nu_distance)
# Matérnカーネルを計算
matern_kernel_matrix = pairwise_kernels(coords, metric=matern_kernel)
# 計算結果を出力
print("\nMatérn Kernel Matrix:")
print(matern_kernel_matrix)出力結果は以下の通りです。
$$
K = \begin{bmatrix}
1.00 & 0.20 & 0.02 & 0.00 \\
0.20 & 1.00 & 0.20 & 0.02 \\
0.02 & 0.20 & 1.00 & 0.20 \\
0.00 & 0.02 & 0.20 & 1.00
\end{bmatrix}
$$
このカーネル行列は、RBFに比べて中距離の点に対しても比較的高い類似度を与えていることが見て取れます。滑らかさの調整ができるため、より柔軟な関数のモデリングが可能です。
周期カーネル(Periodic kernel)
$$ k(x, x’) = \exp\left(-\frac{2\sin^2(\pi|x – x’|/p)}{\lambda^2}\right) $$
このカーネル関数は、周期的に繰り返すようなパターンを持つデータに対して非常に有効です。距離の代わりに $\sin^2$ 関数を用いることで、周期ごとに類似度が高くなるように設計されています。
ハイパーパラメータは $p$ , $\lambda$ です。
- $p$ :周期性の周期を表し、どのくらいの間隔でデータが繰り返されるかを調整します。
- $\lambda$ :周期性のスケールを調整し、周期的な変動の広がりを調整します。
周期カーネルを使用するメリット、デメリットは以下の通りです。
メリット
デメリット
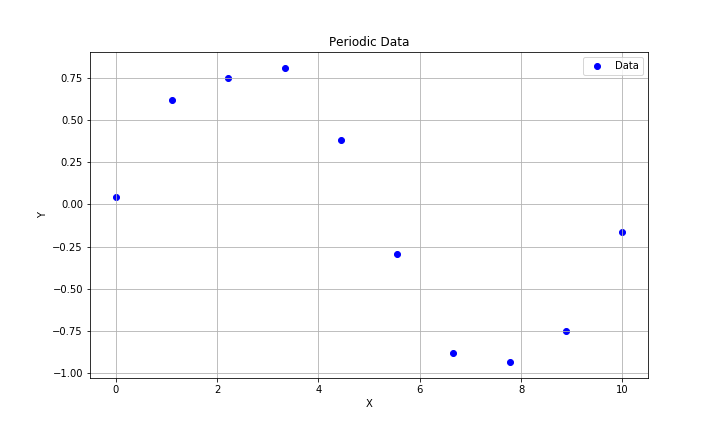
周期カーネルについてもPtyhonにて計算を実行してみました。
計算に使用したのは以下のように周期性のある座標データ10点を使用しています。
実際に使用したコードは以下の通りです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics.pairwise import pairwise_kernels
# 周期性を持つデータを生成する関数
def generate_periodic_data(num_points, period=10, amplitude=1, noise=0.1):
x = np.linspace(0, period, num_points)
y = amplitude * np.sin(2 * np.pi * x / period) + np.random.normal(0, noise, num_points)
return x, y
# 周期性を持つデータの生成
num_points = 10
period = 10
amplitude = 1
noise = 0.1
x, y = generate_periodic_data(num_points, period, amplitude, noise)
# データをプロット
plt.figure(figsize=(10, 6))
plt.scatter(x, y, color='blue', label='Data')
plt.title('Periodic Data')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()
# 周期カーネルの計算
def periodic_kernel(x, y, period=10, gamma=1.0):
return np.exp(-2 * (np.sin(np.pi * np.abs(x - y) / period) ** 2) / gamma ** 2)
# 周期カーネルを計算
periodic_kernel_matrix = pairwise_kernels(x.reshape(-1, 1), metric=periodic_kernel)
# 計算結果を出力
print("Periodic Kernel Matrix:")
print(periodic_kernel_matrix)周期カーネルの結果は以下のように10×10のカーネル共分散行列として出力されます。
$$
K = \begin{bmatrix}
1.00 & 0.79 & 0.44 & 0.22 & 0.14 & 0.14 & 0.22 & 0.44 & 0.79 & 1.00 \\
0.79 & 1.00 & 0.79 & 0.44 & 0.22 & 0.14 & 0.14 & 0.22 & 0.44 & 0.79 \\
0.44 & 0.79 & 1.00 & 0.79 & 0.44 & 0.22 & 0.14 & 0.14 & 0.22 & 0.44 \\
0.22 & 0.44 & 0.79 & 1.00 & 0.79 & 0.44 & 0.22 & 0.14 & 0.14 & 0.22 \\
0.14 & 0.22 & 0.44 & 0.79 & 1.00 & 0.79 & 0.44 & 0.22 & 0.14 & 0.14 \\
0.14 & 0.14 & 0.22 & 0.44 & 0.79 & 1.00 & 0.79 & 0.44 & 0.22 & 0.14 \\
0.22 & 0.14 & 0.14 & 0.22 & 0.44 & 0.79 & 1.00 & 0.79 & 0.44 & 0.22 \\
0.44 & 0.22 & 0.14 & 0.14 & 0.22 & 0.44 & 0.79 & 1.00 & 0.79 & 0.44 \\
0.79 & 0.44 & 0.22 & 0.14 & 0.14 & 0.22 & 0.44 & 0.79 & 1.00 & 0.79 \\
1.00 & 0.79 & 0.44 & 0.22 & 0.14 & 0.14 & 0.22 & 0.44 & 0.79 & 1.00
\end{bmatrix}
$$
この行列は周期的にカーネル値が高くなる位置が現れることを示しており、周期性のあるパターンに対して非常に効果的であることが視覚的に確認できます。
線形カーネル(Linear kernel)
$$ k(x, x’) = x \cdot x’ $$
線形カーネルは、入力ベクトル同士の内積によって類似度を測定するシンプルなカーネル関数です。線形的な関係性を捉えるのに適しています。
内積に基づく単純なカーネルであり、ハイパーパラメータは必要ありません。
線形カーネルを使用するメリット、デメリットは以下の通りです。
メリット
デメリット
実際に線形カーネルについてPythonにより二次元座標間の計算を実行してみました。
同様に(0, 0), (1, 1), (2, 2), (3, 3)の四つの座標について線形カーネルを計算しました。
計算結果は以下のように4×4のマトリクスでカーネルの共分散行列が出力されます。
$$K = \begin{bmatrix}
k((0,0), (0,0)) & k((0,0), (1,1)) & k((0,0), (2,2)) & k((0,0), (3,3)) \\
k((1,1), (0,0)) & k((1,1), (1,1)) & k((1,1), (2,2)) & k((1,1), (3,3)) \\
k((2,2), (0,0)) & k((2,2), (1,1)) & k((2,2), (2,2)) & k((2,2), (3,3)) \\
k((3,3), (0,0)) & k((3,3), (1,1)) & k((3,3), (2,2)) & k((3,3), (3,3))
\end{bmatrix}
$$
使用したコードは以下の通りです。
import numpy as np
from sklearn.metrics.pairwise import linear_kernel
# 二次元座標の例
coords = np.array([[0, 0], [1, 1], [2, 2], [3, 3]])
# 線形カーネルを計算する関数
def linear_kernel_custom(coord1, coord2):
return np.dot(coord1, coord2)
# 線形カーネルを計算
linear_kernel_matrix = linear_kernel(coords)
# 計算結果を出力
print("\nLinear Kernel Matrix:")
print(linear_kernel_matrix)出力結果は以下の通りです。
$$
K = \begin{bmatrix}
2.00 & 4.00 & 6.00 & 8.00 \\
4.00 & 8.00 & 12.00 & 16.00 \\
6.00 & 12.00 & 18.00 & 24.00 \\
8.00 & 16.00 & 24.00 & 32.00
\end{bmatrix}
$$
この行列は、単純にベクトルの内積を表しており、ベクトルの方向や大きさが類似しているほど値が大きくなることを示しています。距離には依存せず、線形関係の評価に特化しています。
多項式カーネル(Polynomial kernel)
$$ k(x, x’) = (x \cdot x’ + c)^d $$
多項式カーネルは内積の多項式によって類似性を評価し、高次元の非線形関係をモデル化します。
また、特定の次数の多項式関数を表現します。
ハイパーパラメータは $d$ , $c$ です。
- $d$ :多項式の次数を制御し、どれだけ複雑な多項式を使用するかを調整します。
- $c$ :調整値であり、単なる内積に一定の値を足してから多項式に変換する役割を持ちます。
多項式カーネルを使用するメリット、デメリットは以下の通りです。
メリット
デメリット
多項式カーネルについてもPythonにより二次元座標間の計算を実行しました。
同様に(0, 0), (1, 1), (2, 2), (3, 3)の四つの座標について多項式カーネルを計算しました。ハイパーパラメータである$d$ と $c$はそれぞれ2, 1.0となっています。
計算結果は以下のように4×4のマトリクスでカーネルの共分散行列が出力されます。
$$K = \begin{bmatrix}
k((0,0), (0,0)) & k((0,0), (1,1)) & k((0,0), (2,2)) & k((0,0), (3,3)) \\
k((1,1), (0,0)) & k((1,1), (1,1)) & k((1,1), (2,2)) & k((1,1), (3,3)) \\
k((2,2), (0,0)) & k((2,2), (1,1)) & k((2,2), (2,2)) & k((2,2), (3,3)) \\
k((3,3), (0,0)) & k((3,3), (1,1)) & k((3,3), (2,2)) & k((3,3), (3,3))
\end{bmatrix}
$$
使用したコードは以下の通りです。
import numpy as np
from sklearn.metrics.pairwise import polynomial_kernel
# 二次元座標の例
coords = np.array([[0, 0], [1, 1], [2, 2], [3, 3]])
# 多項式カーネルのパラメータ(degreeは次数、coef0は定数項)
degree = 2
coef0 = 1.0
# 多項式カーネルを計算する関数
def polynomial_kernel_custom(coord1, coord2):
return (np.dot(coord1, coord2) + coef0) ** degree
# 多項式カーネルを計算
polynomial_kernel_matrix = polynomial_kernel(coords, degree=degree, coef0=coef0)
# 計算結果を出力
print("\nPolynomial Kernel Matrix:")
print(polynomial_kernel_matrix)結果はPolynomial Kernel Matrixとして4×4のマトリクスとして出力されています。
$$
K = \begin{bmatrix}
4.00 & 9.00 & 16.00 & 25.00 \\
9.00 & 25.00 & 49.00 & 81.00 \\
16.00 & 49.00 & 100.00 & 169.00 \\
25.00 & 81.00 & 169.00 & 289.00
\end{bmatrix}
$$
多項式カーネルは、内積に定数を加えてから累乗することで、データの非線形な関係を表現できるカーネルです。
次数 $d$ を大きくすると、より複雑なパターンや特徴の組み合わせも捉えられるようになります。
指数カーネル(Exponential kernel)
$$ k(x, x’) = \exp\left(-\frac{|x – x’|}{2\sigma^2}\right) $$
指数カーネルはデータ間のユークリッド距離を単純な指数関数に適用して評価します。
ガウシアンカーネルと似ていますがユークリッド距離の項が二乗されていません。
ハイパーパラメータは$\sigma$ です。
- $\sigma$ が大きい → 広い範囲のデータを類似とみなす
- $\sigma$ が小さい → 近いデータのみを類似とみなす
指数カーネルを使用するメリット、デメリットは以下の通りです。
メリット
デメリット
指数カーネルについても実際にPythonにより二次元座標間の計算を実行しました。
同様に(0, 0), (1, 1), (2, 2), (3, 3)の四つの座標について指数カーネルを計算しました。ハイパーパラメータである$\sigma$ は0.1で設定しています。
計算結果は以下のように4×4のマトリクスでカーネルの共分散行列が出力されます。
$$K = \begin{bmatrix}
k((0,0), (0,0)) & k((0,0), (1,1)) & k((0,0), (2,2)) & k((0,0), (3,3)) \\
k((1,1), (0,0)) & k((1,1), (1,1)) & k((1,1), (2,2)) & k((1,1), (3,3)) \\
k((2,2), (0,0)) & k((2,2), (1,1)) & k((2,2), (2,2)) & k((2,2), (3,3)) \\
k((3,3), (0,0)) & k((3,3), (1,1)) & k((3,3), (2,2)) & k((3,3), (3,3))
\end{bmatrix}
$$
使用したコードは以下の通りです。
import numpy as np
from sklearn.metrics.pairwise import pairwise_kernels
# 二次元座標の例
coords = np.array([[0, 0], [1, 1], [2, 2], [3, 3]])
# 指数カーネルのパラメータ(gammaはバンド幅)
gamma = 0.1
# 指数カーネルを計算する関数
def exponential_kernel(coord1, coord2):
return np.exp(-gamma * np.linalg.norm(coord1 - coord2))
# 指数カーネルを計算
exponential_kernel_matrix = pairwise_kernels(coords, metric=exponential_kernel)
# 計算結果を出力
print("Exponential Kernel Matrix:")
print(exponential_kernel_matrix)結果はExponential Kernel Matrixとして4×4のマトリクスとして出力されます。
$$
K = \begin{bmatrix}
1.00 & 0.87 & 0.75 & 0.65 \\
0.87 & 1.00 & 0.87 & 0.75 \\
0.75 & 0.87 & 1.00 & 0.87 \\
0.65 & 0.75 & 0.87 & 1.00
\end{bmatrix}
$$
この行列では、距離が離れるほど値が滑らかに減衰する様子が見られます。ガウシアンカーネルよりも穏やかな減衰を示し、近傍以外の点も一定の影響を受けます。
オススメの書籍
最後にガウス過程回帰やカーネル関数ついてもっと知りたい方に向けてオススメの書籍をご紹介します。
ご紹介する
『Pythonで学ぶ実験計画法入門 ベイズ最適化によるデータ解析』
は、特に材料開発やプロセス開発における実験計画法に焦点を当てた、非常に実践的な内容となっています。
本書の特徴として
- ベイズ最適化の基本概念の解説
- 獲得関数やガウス過程回帰の詳細な解説
- 実際に使えるPythonコードとデータセットをGitHubからダウンロード可能
という点から、実際に手を動かしながらベイズ最適化を学ぶことができ理解がぐっと深まります。
特に、材料やプロセスの最適化を効率的に進めたいと考えている方には、本書のアプローチは非常に実用的で、すぐに現場に活かせる内容だと感じました。
さらに、ベイズ最適化以外にも、機械学習を活用したデータ解析手法について幅広く解説されているため、実験設計からデータ解析まで一貫して学びたい方にもぴったりです。
材料開発の現場で、データを最大限に活用したいと考えている方に、ぜひ手に取っていただきたい一冊です。
ベイズ最適化のオススメ参考書については以下の記事でもまとめていますので、興味のある方はご参照いただければと思います。
終わりに
以上がカーネルについてとそれぞれのカーネルの特徴に関する説明になります。色々なカーネルの種類があるので、交差検証などでそのモデルに適したカーネルを選択する必要がありそうですね。
カーネルの数式まで詳細に理解するかはさておき、カーネルがどの指標で類似度を評価しているかはしっかりと把握する必要がありますね。