こんにちは!ぼりたそです!
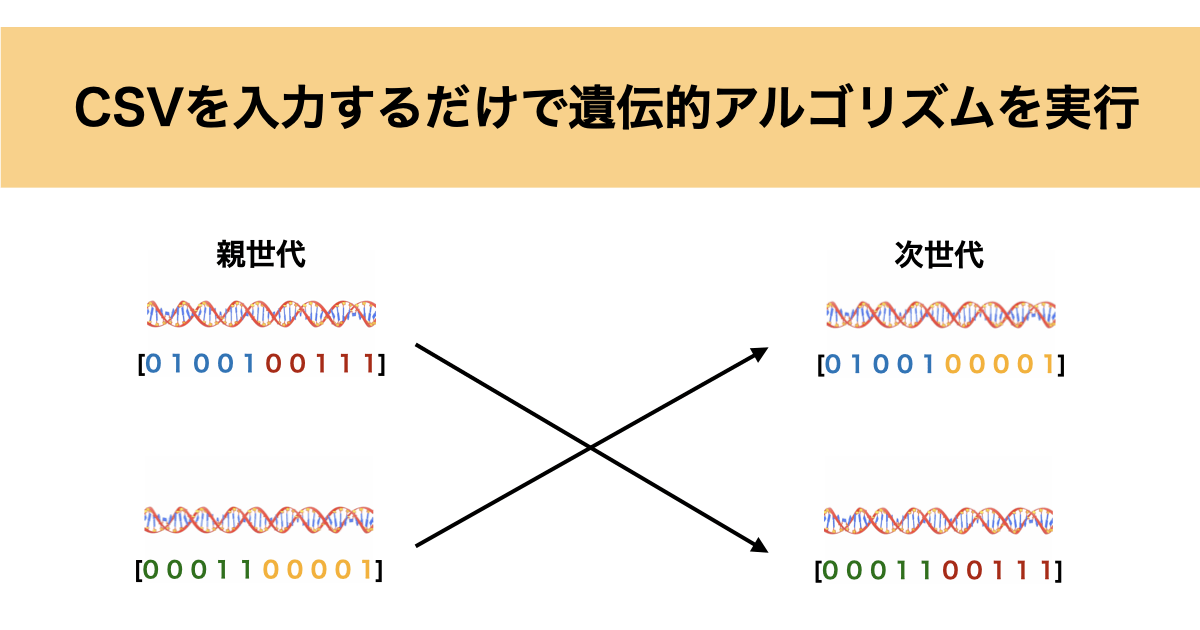
今回は初期データのCSVファイルを入力するだけで遺伝的アリゴリズムを実行するコードを実装しましたのでご紹介したいと思います。
この記事は以下のポイントでまとめています。
- 遺伝的アルゴリズムとは?
- 実装コードの流れ
- 実装コードと解説
以下、詳細に解説していきます。
遺伝的アルゴリズムとは?
まずは遺伝的アルゴリズムについて簡単に説明していきます。
遺伝的アルゴリズム(Genetic Algorithm, GA)は、生物の進化に着想を得た最適化手法で、人工知能や機械学習、組み合わせ最適化問題などで広く利用されています。
GAは主に「自然選択」「遺伝子操作」を模倣して解を進化させることで、最適解やそれに近い解を探索することが可能です。
例えば、以下のような問題を解決する場合にGAが役立ちます。
- ナップサック問題:
複数のアイテムを限られた容量のナップサックに詰める問題で、最大の価値を得る組み合わせを探します。
- スケジューリング問題:
例えば、ジョブをマシンに効率よく割り当てる問題。GAを使用することで複数の制約条件を満たしつつ、最適なスケジュールを見つけることができます。
- 迷路解決:
GAを使って、迷路を効率的に解くための最適なパスを見つけることができます。
- フィーチャー選択:
大量のデータから重要な特徴量を選び出す問題にGAが使われることがあります。
上記の問題で遺伝的アルゴリズムが使用される理由は、GAが広範な探索空間を効率的に探索し、複数の局所最適解に対してグローバル最適解を見つけるのに適しているためです。
さらに、GAは並列計算に向いており、複数の解を同時に探索することで、高度に複雑な問題にも対応できる強力なツールとなります。
遺伝的アルゴリズムの基礎については以下の記事にまとめてありますので、参照いただければと思います。
実装コードの流れ
次に今回実装したコードの大まかな流れについて説明していきます。
コードとしては既存データをインプットデータとすることで次世代の推奨データがアウトプットデータとして出力されるようになっています。
入力データと出力データについての詳細は以下の通りです。
- 入力データ
一列目に目的変数(適応度)、二列目以降に説明変数を記載したCSVファイルとして下さい。なお、一行目(ヘッダー)は目的変数および説明変数名を記載するようにして下さい。
- 出力データ
一列目に目的変数(適応度)の空列、二列目以降に次世代の説明変数が記載されたCSVファイルとなっています。一列目に目的変数の値を入力することで再度入力データとして使用することができ、遺伝的アルゴリズムの最適化サイクルを回すことができます。
また、コードにはいくつかのハイパーパラメータがあり、問題に合わせて適宜変更するようにして下さい。ハイパーパラメータの詳細は後ほど説明します。
実装コードと解説
次に実装コードとその解説をしていきます。
今回実装したコードは以下の通りとなります。
import csv
import random
import numpy as np
import pandas as pd
# パラメータ設定
population_size = 50 # 集団のサイズ(初期集団はCSVのデータを使用するので無視)
genome_length = None # 後でデータの次元から自動設定
crossover_rate = 0.8 # 交叉の確率
mutation_rate = 0.01 # 突然変異の確率
max_generations = 1 # 最大世代数は1
selection_method = "tournament" # 選択手法: "roulette"、"tournament"、"elite"
crossover_method = "two_point" # 交叉手法: "one_point"、"two_point"
mutation_method = "gaussian" # 突然変異手法: "single_bit"、"random_reset"、"gaussian"
# CSVファイルのパスを指定
input_csv = "input_data.csv" # 入力データCSV(1列目は目的変数(適応度)、2列目以降は説明変数)
output_csv = "next_generation.csv" # 次世代の出力先
# 選択: ルーレット選択
def roulette_selection(population, fitness_values):
max_fitness = sum(fitness_values)
pick = random.uniform(0, max_fitness)
current = 0
for ind, fitness_value in zip(population, fitness_values):
current += fitness_value
if current > pick:
return ind
# 選択: トーナメント選択
def tournament_selection(population, fitness_values, k=3):
selected = random.sample(list(zip(population, fitness_values)), k)
return max(selected, key=lambda x: x[1])[0]
# 選択: エリート選択
def elite_selection(population, fitness_values, elite_ratio=0.1):
elite_size = int(len(population) * elite_ratio)
sorted_population = [x for _, x in sorted(zip(fitness_values, population), reverse=True)]
return sorted_population[:elite_size]
# 交叉: 1点交叉
def one_point_crossover(parent1, parent2):
if random.random() < crossover_rate:
point = random.randint(1, len(parent1) - 1)
return np.concatenate((parent1[:point], parent2[point:])), np.concatenate((parent2[:point], parent1[point:]))
return parent1, parent2
# 交叉: 2点交叉
def two_point_crossover(parent1, parent2):
if random.random() < crossover_rate:
point1 = random.randint(1, len(parent1) - 2)
point2 = random.randint(point1 + 1, len(parent1) - 1)
return (np.concatenate((parent1[:point1], parent2[point1:point2], parent1[point2:])),
np.concatenate((parent2[:point1], parent1[point1:point2], parent2[point2:])))
return parent1, parent2
# 突然変異: 単一ビット変異 (バイナリ値)
def single_bit_mutation(individual):
for i in range(len(individual)):
if random.random() < mutation_rate:
individual[i] = 1 - individual[i] # ビットを反転させる
return individual
# 突然変異: ランダムリセット (連続値用)
def random_reset_mutation(individual, min_max_pairs):
for i in range(len(individual)):
if random.random() < mutation_rate:
min_val, max_val = min_max_pairs[i]
# リセットの際に最小値と最大値の範囲で新しい値を生成
individual[i] = random.uniform(min_val, max_val) # int も float も扱える
return individual
# 突然変異: ガウス突然変異 (連続値)
def gaussian_mutation(individual, mean_std_pairs):
for i in range(len(individual)):
if random.random() < mutation_rate:
mean, stddev = mean_std_pairs[i]
individual[i] += np.random.normal(mean, stddev)
return individual
# 遺伝的アルゴリズム
def genetic_algorithm(population, fitness_values, min_max_pairs, mean_std_pairs, selection_method, crossover_method, mutation_method):
next_generation = []
# エリート選択
if selection_method == "elite":
elites = elite_selection(population, fitness_values)
next_generation.extend(elites)
# 交叉と突然変異
while len(next_generation) < len(population):
# 選択メソッド選択
if selection_method == "roulette":
parent1 = roulette_selection(population, fitness_values)
parent2 = roulette_selection(population, fitness_values)
elif selection_method == "tournament":
parent1 = tournament_selection(population, fitness_values)
parent2 = tournament_selection(population, fitness_values)
elif selection_method == "elite":
parent1 = random.choice(elites)
parent2 = random.choice(elites)
# 交叉メソッド選択
if crossover_method == "one_point":
offspring1, offspring2 = one_point_crossover(parent1, parent2)
elif crossover_method == "two_point":
offspring1, offspring2 = two_point_crossover(parent1, parent2)
# 突然変異メソッド選択
if mutation_method == "single_bit":
offspring1 = single_bit_mutation(offspring1)
offspring2 = single_bit_mutation(offspring2)
elif mutation_method == "random_reset":
offspring1 = random_reset_mutation(offspring1, min_max_pairs)
offspring2 = random_reset_mutation(offspring2, min_max_pairs)
elif mutation_method == "gaussian":
offspring1 = gaussian_mutation(offspring1, mean_std_pairs)
offspring2 = gaussian_mutation(offspring2, mean_std_pairs)
next_generation.append(offspring1)
next_generation.append(offspring2)
return next_generation[:len(population)]
# CSVファイルを読み込んでGAを実行
def run_ga_from_csv(input_csv, output_csv, selection_method, crossover_method, mutation_method):
data = pd.read_csv(input_csv)
# ヘッダーを取得
header = data.columns.tolist()
# 説明変数(2列目以降を初期集団として使用)
x = data.iloc[:, 1:].values # 説明変数(1列目は適応度で無視)
fitness_values = data.iloc[:, 0].values # 1列目を適応度として使用
global genome_length
genome_length = x.shape[1]
# 各列の最小値と最大値を計算(ランダムリセットに使用)
min_max_pairs = []
for col in data.iloc[:, 1:].columns:
min_val = data[col].min()
max_val = data[col].max()
min_max_pairs.append((min_val, max_val))
# 各列の平均と標準偏差を計算(連続値のガウス変異に使用)
mean_std_pairs = []
for col in data.iloc[:, 1:].columns:
mean = data[col].mean()
stddev = data[col].std()
mean_std_pairs.append((mean, stddev))
# 遺伝的アルゴリズムを実行
next_population = genetic_algorithm(x, fitness_values, min_max_pairs, mean_std_pairs, selection_method, crossover_method, mutation_method)
# 結果をCSVに書き出す(目的変数列は空白)
result = pd.DataFrame(next_population)
result.insert(0, '', '') # 1列目を空白にする
result.to_csv(output_csv, index=False, header=header) # input_data.csvのヘッダーを使用
if __name__ == "__main__":
run_ga_from_csv(input_csv, output_csv, selection_method=selection_method, crossover_method=crossover_method, mutation_method=mutation_method)
実装コードは大きく以下の構成で作成しています。
- ハイパーパラメータ設定
- 関数の定義_選択
- 関数の定義_交叉
- 関数の定義_突然変異
- 関数の定義_遺伝的アルゴリズム
- 関数の定義_CSVを読み込み遺伝的アルゴリズム実行
それでは、順に解説していきます。
ハイパーパラメータの設定
まずはハイパーパラメータの設定についてです。
実装コードの中では以下の部分で処理しています。
# パラメータ設定
population_size = 50 # 集団のサイズ(初期集団はCSVのデータを使用するので無視)
genome_length = None # 後でデータの次元から自動設定
crossover_rate = 0.8 # 交叉の確率
mutation_rate = 0.01 # 突然変異の確率
max_generations = 1 # 最大世代数は1
selection_method = "tournament" # 選択手法: "roulette"、"tournament"、"elite"
crossover_method = "two_point" # 交叉手法: "one_point"、"two_point"
mutation_method = "single_bit" # 突然変異手法: "single_bit"、"random_reset"、"gaussian"
# CSVファイルのパスを指定
input_csv = "input_data.csv" # 入力データCSV(1列目は目的変数(適応度)、2列目以降は説明変数)
output_csv = "next_generation.csv" # 次世代の出力先この部分では基本的に次世代生成時に必要なハイパーパラメータを設定するコードとなっています。
ハイパーパラメータについて詳細は以下の通りになっています。
| 変数名(ハイパーパラメータ) | 変数の説明 |
|---|---|
| population_size | 次世代の集団サイズ。いくつの次世代を生成したいかを数値で入力。 |
| genome_length | 遺伝子の長さであり、説明変数の個数に該当。インプットデータから自動で設定されるため、デフォルトのNoneで変更不要。 |
| crossover_rate | 交叉が起こる確率。0.0~1.0の任意の割合で設定 |
| mutation_rate | 突然変異が起こる確率。0.0~1.0の任意の割合で設定 |
| max_generations | 最大世代数の変数。基本的に1世代ずつ生成することを想定しているため、デフォルトの1から変更不要 |
| selection_method | 次世代生成法である「選択」の手法。ルーレット選択 :”roulette”、トーナメント選択: “tournament”、エリート選択:”elite”の3つから選ぶ |
| crossover_method | 次世代生成法である「交叉」の手法。一点交叉:”one_point”、二点交叉:”two_point”から選択可能。 |
| mutation_method | 次世代生成法である「突然変異」の手法。ビット変換突然変異:”single_bit”、ランダムリセット突然変異:”random_reset”、ガウス突然変異:”gaussian”の3つから選択可能。 |
また、input_csv, output_csvにはそれぞれ入力ファイルと出力ファイルのパスを設定するようにして下さい。
関数の定義_選択
次に次世代生成手法である選択の関数についてです。
実装コードの中では以下の部分で処理しています。
# 選択: ルーレット選択
def roulette_selection(population, fitness_values):
max_fitness = sum(fitness_values)
pick = random.uniform(0, max_fitness)
current = 0
for ind, fitness_value in zip(population, fitness_values):
current += fitness_value
if current > pick:
return ind
# 選択: トーナメント選択
def tournament_selection(population, fitness_values, k=3):
selected = random.sample(list(zip(population, fitness_values)), k)
return max(selected, key=lambda x: x[1])[0]
# 選択: エリート選択
def elite_selection(population, fitness_values, elite_ratio=0.05):
elite_size = int(len(population) * elite_ratio)
sorted_population = [x for _, x in sorted(zip(fitness_values, population), reverse=True)]
return sorted_population[:elite_size]まず、関数の引数について登場するものを以下に示します。
| 引数名 | 説明 |
|---|---|
| population | インプットした説明変数。デフォルトのままでOK。 |
| fitness_value | インプットした目的変数(適応度)。デフォルトのままでOK |
| k | トーナメントに参加する個体の数。デフォルトは3です。ランダムに選ばれたk個の個体の中で、最も適応度が高いものを選択します。変更したければ引数を設定して下さい。 |
| elite_ratio | エリートとして残す個体の割合。0.05は、全個体の5%をエリートとして次世代に残すことになります。変更したければ引数を設定して下さい。 |
ルーレット選択はpopulation, fitness_valueを引数として実行します。目的変数の合計値をmax_fitnessとして0からmax_fitnessの間の数値をランダムで選択し、pickの変数に格納しています。あとは目的変数を順に足し合わせていき、pickの値を超えたら終了とし、超えた時の個体を次世代の個体として選択します。
トーナメント選択はpopulation, fitness_value, kを引数として実行します。ランダムに選択されたk個のトーナメントで最も大きい目的変数の個体を次世代として選択します。
エリート選択はpopulation, fitness_values, elite_ratioを変数として実行します。こちらは単純にelito_ratioで設定したの割合、例えば0.05であれば上位5%の個体をそのまま次世代へ選択します。
関数の定義_交叉
次は交叉の関数定義について説明していきます。
実装コードの中では以下の部分で処理しています。
# 交叉: 1点交叉
def one_point_crossover(parent1, parent2):
if random.random() < crossover_rate:
point = random.randint(1, len(parent1) - 1)
return np.concatenate((parent1[:point], parent2[point:])), np.concatenate((parent2[:point], parent1[point:]))
return parent1, parent2
# 交叉: 2点交叉
def two_point_crossover(parent1, parent2):
if random.random() < crossover_rate:
point1 = random.randint(1, len(parent1) - 2)
point2 = random.randint(point1 + 1, len(parent1) - 1)
return (np.concatenate((parent1[:point1], parent2[point1:point2], parent1[point2:])),
np.concatenate((parent2[:point1], parent1[point1:point2], parent2[point2:])))
return parent1, parent2まず、引数について詳細を以下のテーブルに記載します。
| 引数名 | 説明 |
|---|---|
| parent1 | 交叉に使用される親の個体その1。親世代からルーレット選択により設定されるので、デフォルトのままでOK。 |
| parent2 | 交叉に使用される親の個体その2。親世代からルーレット選択により設定されるのでデフォルトのままでOK。 |
一点交叉、二点交叉共にランダム関数にて交叉点を決定し、parent1, parent2の配列を交叉する関数になっています。
関数の定義_突然変異
次は突然変異の関数定義について説明していきます。
実装コードの中では以下の部分で処理しています。
# 突然変異: 単一ビット変異 (バイナリ値)
def single_bit_mutation(individual):
for i in range(len(individual)):
if random.random() < mutation_rate:
individual[i] = 1 - individual[i] # ビットを反転させる
return individual
# 突然変異: ランダムリセット (連続値用)
def random_reset_mutation(individual, min_max_pairs):
for i in range(len(individual)):
if random.random() < mutation_rate:
min_val, max_val = min_max_pairs[i]
# リセットの際に最小値と最大値の範囲で新しい値を生成
individual[i] = random.uniform(min_val, max_val) # int も float も扱える
return individual
# 突然変異: ガウス突然変異 (連続値)
def gaussian_mutation(individual, mean_std_pairs):
for i in range(len(individual)):
if random.random() < mutation_rate:
mean, stddev = mean_std_pairs[i]
individual[i] += np.random.normal(mean, stddev)
return individualまず、引数について以下のテーブルに記載します。
| 引数名 | |
|---|---|
| individual | 突然変異を起こす個体の説明変数。自動で設定されるのでデフォルトのままでOK。 |
| min_max_pairs | ランダムリセットで使用する引数。各変数の最小値、最大値のタプルであり、ランダムリセットする数値の範囲として使用する。自動で設定されるのでデフォルトのままでOK。 |
| mean_std_pairs | ガウス突然変異で使用する引数。各変数の平均と分散のタプルであり、ガウス突然変異を起こす数値の範囲として使用する。自動で設定されるのでデフォルトのままでOK。 |
単一ビット突然変異についてはバイナリビットデータ専用の関数となっています。individualとして設定された個体に対して各ビットが一定の確率で反転するようになっています。
ランダムリセット突然変異については連続値データ専用の関数となっています。individualとして設定された個体に対して各ビットが一定の確率でmin_valとmax_valの範囲で変化するようになっています。
ガウス突然変異については連続値データ専用の関数となっています。individualとして設定された個体に対して各ビットが一定の確率でmean, stddevに従う正規分布の値の範囲でへんかするようになっています。
関数の定義_遺伝的アルゴリズム
次に遺伝的アルゴリズムの関数定義について説明します。
実装コードの中では以下の部分で処理しています。
# 遺伝的アルゴリズム
def genetic_algorithm(population, fitness_values, min_max_pairs, mean_std_pairs, selection_method, crossover_method, mutation_method):
next_generation = []
# エリート選択
if selection_method == "elite":
elites = elite_selection(population, fitness_values)
next_generation.extend(elites)
# 交叉と突然変異
while len(next_generation) < len(population):
# 選択メソッド選択
if selection_method == "roulette":
parent1 = roulette_selection(population, fitness_values)
parent2 = roulette_selection(population, fitness_values)
elif selection_method == "tournament":
parent1 = tournament_selection(population, fitness_values)
parent2 = tournament_selection(population, fitness_values)
elif selection_method == "elite":
parent1 = random.choice(elites)
parent2 = random.choice(elites)
# 交叉メソッド選択
if crossover_method == "one_point":
offspring1, offspring2 = one_point_crossover(parent1, parent2)
elif crossover_method == "two_point":
offspring1, offspring2 = two_point_crossover(parent1, parent2)
# 突然変異メソッド選択
if mutation_method == "single_bit":
offspring1 = single_bit_mutation(offspring1)
offspring2 = single_bit_mutation(offspring2)
elif mutation_method == "random_reset":
offspring1 = random_reset_mutation(offspring1, min_max_pairs)
offspring2 = random_reset_mutation(offspring2, min_max_pairs)
elif mutation_method == "gaussian":
offspring1 = gaussian_mutation(offspring1, mean_std_pairs)
offspring2 = gaussian_mutation(offspring2, mean_std_pairs)
next_generation.append(offspring1)
next_generation.append(offspring2)
return next_generation[:len(population)]まず、引数の説明を以下のテーブルに記載します。
| 引数名 | 説明 |
|---|---|
| population | インプットした親世代の説明変数。デフォルトのままでOK。 |
| fitness | インプットした親世代の目的変数(適応度)。デフォルトのままでOK |
| min_max_pairs | ランダムリセットで使用する引数。各変数の最小値、最大値のタプルであり、ランダムリセットする数値の範囲として使用する。自動で設定されるのでデフォルトのままでOK。 |
| mean_std_pairs | ガウス突然変異で使用する引数。各変数の平均と分散のタプルであり、ガウス突然変異を起こす数値の範囲として使用する。自動で設定されるのでデフォルトのままでOK。 |
| selection_method | 次世代生成法である「選択」の手法。ルーレット選択 :”roulette”、トーナメント選択 : “tournament”、エリート選択:”elite”の3つから選ぶ |
| crossover_method | 次世代生成法である「交叉」の手法。一点交叉:”one_point”、二点交叉:”two_point”から選択可能。 |
| mutation_method | 次世代生成法である「突然変異」の手法。ビット変換突然変異:”single_bit”、ランダムリセット突然変異:”random_reset”、ガウス突然変異:”gaussian”の3つから選択可能。 |
この関数は遺伝的アルゴリズムを実行する関数であり、次世代生成を行います。
まずは選択でエリート選択を設定している場合はelite_selectionによりエリート選択が実行されます。
それ以降は、選択により親世代を選択し、任意の確率で交叉や突然変異が起こるようになっており、これを設定した次世代個体数に達するまで繰り返します。
関数の定義_CSVを読み込み遺伝的アルゴリズムを実行
最後にCSVを入力して遺伝的アルゴリズムを実行する関数定義について説明します。
実装コードの中では以下の部分で処理しています。
# CSVファイルを読み込んでGAを実行
def run_ga_from_csv(input_csv, output_csv, selection_method, crossover_method, mutation_method):
data = pd.read_csv(input_csv)
# ヘッダーを取得
header = data.columns.tolist()
# 説明変数(2列目以降を初期集団として使用)
x = data.iloc[:, 1:].values # 説明変数(1列目は適応度で無視)
fitness_values = data.iloc[:, 0].values # 1列目を適応度として使用
global genome_length
genome_length = x.shape[1]
# 各列の最小値と最大値を計算(ランダムリセットに使用)
min_max_pairs = []
for col in data.iloc[:, 1:].columns:
min_val = data[col].min()
max_val = data[col].max()
min_max_pairs.append((min_val, max_val))
# 各列の平均と標準偏差を計算(連続値のガウス変異に使用)
mean_std_pairs = []
for col in data.iloc[:, 1:].columns:
mean = data[col].mean()
stddev = data[col].std()
mean_std_pairs.append((mean, stddev))
# 遺伝的アルゴリズムを実行
next_population = genetic_algorithm(x, fitness_values, min_max_pairs, mean_std_pairs, selection_method, crossover_method, mutation_method)
# 結果をCSVに書き出す(目的変数列は空白)
result = pd.DataFrame(next_population)
result.insert(0, '', '') # 1列目を空白にする
result.to_csv(output_csv, index=False, header=header) # input_data.csvのヘッダーを使用まずは引数について以下のテーブルに記載します。
| 引数名 | 説明 |
|---|---|
| input_csv | 入力するCSVファイルのパス。 |
| output_csv | 出力するCSVファイルのパス。 |
| seloction_method | 次世代生成法である「選択」の手法。ルーレット選択 :”roulette”、トーナメント選択 : “tournament”、エリート選択:”elite”の3つから選ぶ |
| crossover_method | 次世代生成法である「交叉」の手法。一点交叉:”one_point”、二点交叉:”two_point”から選択可能。 |
| mutation_method | 次世代生成法である「突然変異」の手法。ビット変換突然変異:”single_bit”、ランダムリセット突然変異:”random_reset”、ガウス突然変異:”gaussian”の3つから選択可能。 |
今まで定義してきた関数について、この関数を使用して実行することになります。
基本的にはinput_csvから説明変数名や説明変数の数を読み取ります。さらに各変数の最大値と最小値、平均と分散などを抽出します。
最終的に抽出したデータからgenetic_algorithmの関数を使用して遺伝的アルゴリズムを実行し、次世代集団を生成しています。
生成した次世代集団をCSVファイルに保存したら完了になります。
終わりに
以上がCSVファイルを入力するだけで遺伝的アルゴリズムを実行するPythonコードの解説になります。まだまだ改造の余地はありますが、ひとまず遺伝的アルゴリズムがどうやって動くのか理解できるコードになっているのではないでしょうか。Pythonで遺伝的アルゴリズムを実行したい方はぜひ参考にしていいただければと思います。