こんにちは!ぼりたそです!
今回はPythonのGpyOptというライブラリを使用してベイズ最適化を実行する手法について解説していきます。
この記事は以下のポイントでまとめています。
- GPyOptとは?
- ベイズ最適化のフロー
- 実装コードと解説
それでは詳細に解説していきます。
GpyOptとは?
まずはGPyOptについてご紹介していきます。
GPyOptは、ベイズ最適化(Bayesian Optimization)のためのPythonライブラリで、ベイズ最適化を容易に実装できるように設計されています。
ベイズ最適化とは機械学習の手法の一つであり、現状のデータから効率的に目標値を達成できる最適化手法となっています。
詳しくは以下の記事にまとめてありますので、ご参考いただければと思います。
GPyOptの主な特徴は以下の通りです。
■GPyOptの特徴
ベイズ最適化のフロー
次に今回実装するベイズ最適化のフローについてご説明します。
本記事では以下の関数について最大点を見つけるために最適化を実行していきます。
$$f(x) = \sin(x) \cdot \cos(x) \cdot x^{-1}$$
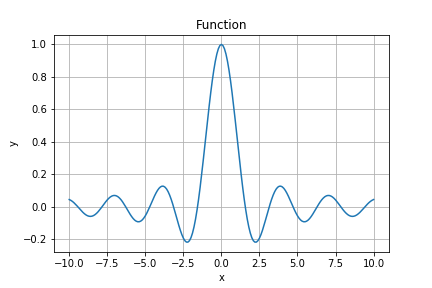

最大値となるのがx=0の時ですが、果たして最適化で導き出せるのでしょうか?というのが今回のお題ですね。
具体的な条件については以下の通りとなります。
| 目標値 | $f(x) = \sin(x) \cdot \cos(x) \cdot x^{-1}$の最大化 |
| 学習データ(初期データ) | x=(-7, -6.5, -6, -5.5, -5, -4.5, -4) |
| 学習モデル | ガウス過程回帰(GP) |
| カーネル | RBF |
| 獲得関数 | EI |
実装コード
それでは実際にベイズ最適化の実装コードとその解説をしていきます。
まず、GPyOptをインストールしていなければ以下のコードを実行してください。
pip install GPyOpt
pip install GPy次に最適化を実行するコードですが、以下のコードで実装しています。
import GPy
import GPyOpt
import numpy as np
trial = 1
# -2から2まで0.1刻みの数値を含む配列を作成
pre_x = np.arange(-7, -4, 0.2)
pre_x = pre_x.reshape(-1,1)
# 関数の計算
pre_y = np.cos(pre_x) * pre_x**-1 * np.sin(pre_x) # 例としてsin関数を使用
pre_y = pre_y.reshape(-1,1)
# 目的関数の定義
def objective_function(x):
global pre_y, pre_x, trial
print(f'trial : {trial}')
trial += 1
#候補のxを出力して学習データに追加する
print('x :',x)
pre_x = np.append(pre_x,x)
pre_x = pre_x.reshape(-1,1)
#候補のxからyを計算して学習データに追加する
y = np.cos(x) * x**-1 * np.sin(x)
print('y :',y)
pre_y = np.append(pre_y,y)
pre_y = pre_y.reshape(-1,1)
return y
# 探索領域の設定
domain = [{'name': 'x', 'type': 'continuous', 'domain': (-10, 10)}]
# BayesianOptimizationオブジェクトの作成
bo = GPyOpt.methods.BayesianOptimization(f=objective_function,
model_type='GP',
domain=domain,
acquisition='EI',
maximize = True,
X=pre_x,
Y=pre_y)
# ベイズ最適化の実行(yが0.99以上になるまで繰り返す)
while np.max(pre_y)<0.99:
# 1つの候補点を出力
bo.run_optimization(max_iter=1)
bo.plot_acquisition() #ガウス過程回帰のプロットと獲得関数のグラフを表示
#出力結果
#trial : 1
#x : [[10.]]
#y : [[0.04564726]]
#trial : 2
#x : [[6.12281422]]
#y : [[-0.02574559]]
#trial : 3
#x : [[-10.]]
#y : [[0.04564726]]
#trial : 4
#x : [[2.01567796]]
#y : [[-0.19271995]]
#trial : 5
#x : [[8.35341097]]
#y : [[-0.05032997]]
#trial : 6
#x : [[-9.04815013]]
#y : [[-0.03779874]]
#trial : 7
#x : [[-0.83117423]]
#y : [[0.59903928]]
#trial : 8
#x : [[-0.49667406]]
#y : [[0.84346902]]
#trial : 9
#x : [[0.06836471]]
#y : [[0.99688709]]結果としては9回のベイズ最適化で最高値までたどり着いています。
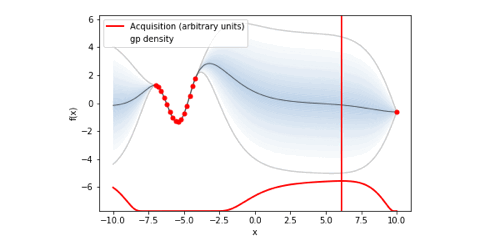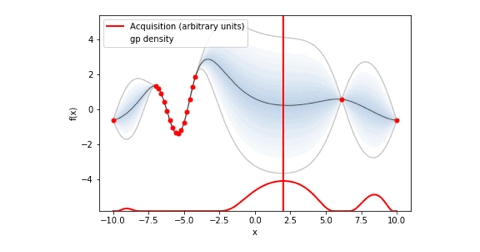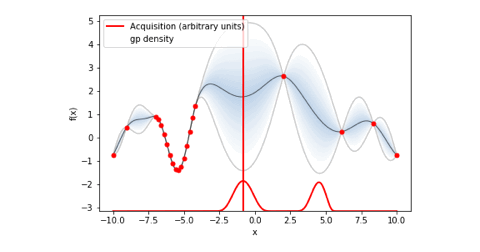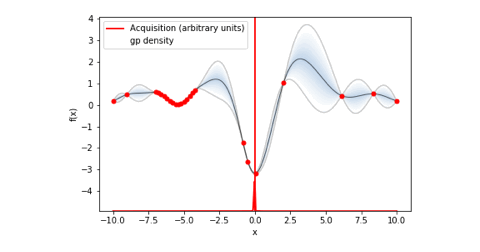
bo.plot_acquisition()で出力されたガウス過程回帰と獲得関数のグラフを下にgif画像として載せておきました。
ちなみにmaximize = True(目的変数の最大化)としていることで関数に-1がかけられているので、関数の正負が逆転しています。

コードの解説
それでは実装したコードについて解説していきます。
GPyOptでベイズ最適化を実行するには大きく以下のステップでコードを作成します。
- 目的関数の定義
- 探索領域の定義
- ベイズ最適化のオブジェクト生成
- ベイズ最適化の実行
- 学習モデルの可視化
目的関数の定義
まずは目的関数の定義について説明します。
GPyOptでベイズ最適化を実行する場合、目的関数を定義する必要があります。
今回は以下の関数を設定していました。
# 目的関数の定義
def objective_function(x):
global pre_y, pre_x, trial
print(f'trial : {trial}')
trial += 1
#候補のxを出力して学習データに追加する
print('x :',x)
pre_x = np.append(pre_x,x)
pre_x = pre_x.reshape(-1,1)
#候補のxからyを計算して学習データに追加する
y = np.cos(x) * x**-1 * np.sin(x)
print('y :',y)
pre_y = np.append(pre_y,y)
pre_y = pre_y.reshape(-1,1)
return y基本的には説明変数xを引数とした関数を定義する必要があり、今回は候補とするxを学習データに追加→xから関数yを算出→yも学習データに追加する→yを返り値とする関数を設定しています。
実際に実験して測定値を入力したい場合は以下のように関数を設定するといいと思います。
実問題の最適化については最適化したい関数の形なんて分かりませんので、提案されたxに対して目的変数であるyを入力する様な関数にするとGPyOptでも対応できるかと思います。
とりあえず、何かしらの関数を設定しないと最適化が実行できないので注意しましょう。
#実際に実験して測定値を入力したい場合
def objective_function(x):
print(x)
y = float(input('実験値は?'))
return y探索領域の定義
次に探索領域の定義について説明します。
探索領域とは学習モデルから次の候補点を探す変数空間のことを指します。
今回の実装コードでは以下の様に記述されています。
# 探索領域の設定
domain = [{'name': 'x', 'type': 'continuous', 'domain': (-10, 10)}]リストの中に辞書形式としてKeyとValueを設定していきます。KeyとValueの設定方法は以下の通りです。
| Key | Value |
|---|---|
| name | 変数名を設定 |
| type | 探索空間が連続値の場合はcontinuous、離散値の場合はdiscreteと設定する |
| domain | 探索領域の範囲を設定。 ex) (-10,10)→-10から10まで(連続値) [-10, -10,]→-10, -10のみ(離散値) |
また、今回は変数が1つでしたが、複数ある場合はリスト内の辞書を増やしていけば大丈夫です。
# 探索領域の設定(変数が複数ある場合)
domain = [{'name': 'x1', 'type': 'continuous', 'domain': (-10, 10)},
{'name': 'x2', 'type': 'continuous', 'domain': (5, 100)},
{'name': 'x3', 'type': 'discrete', 'domain': (-10, -5, 0)}]ベイズ最適化オブジェクトの生成
次にベイズ最適化オブジェクト生成について説明していきます。
これはベイズ最適化を実行するにあたり細かい設定をしていく作業になります。
今回は以下の様なコードで実行しています。
# BayesianOptimizationオブジェクトの作成
bo = GPyOpt.methods.BayesianOptimization(f=objective_function,
model_type='GP',
domain=domain,
acquisition='EI',
maximize = True,
X=pre_x,
Y=pre_y)BayesianOptimizationのメソッドは上記コードで設定されている引数以外にも多くあります。今回は頻繁に使用する引数とその設定値については以下にまとめています。
| 引数 | 設定値 |
|---|---|
| f | 設定した目的関数 |
| domain | 変数ごとに設定した探索領域 |
| constraction | 変数ごとに設定した変数の制約条件 |
| model_type | ガウス過程回帰の種類を設定する。通常は’GP’だが、’GP_MCMC’, ‘sparseGP’, ‘warperdGP’も選択可能(デフォルトはGP) |
| X | 初期データ(学習データ)の説明変数 |
| Y | 初期データ(学習データ)の目的変数 |
| initial_design_numdata | 初期データ(学習データ)のデータ数 |
| acquisition_type | 獲得関数の設定。’EI’, ‘MPI’, ‘LCB’から選択可能(デフォルトはEI) |
| maximizer | Trueと設定すれば獲得関数を最大化する。(デフォルトはFalse) |
ベイズ最適化の実行
次にベイズ最適化の実行について解説します。
ここまで来ればそこまで難しいことはありません。
今回のコードでは以下の部分で実行しています。
# 1つの候補点を出力
bo.run_optimization(max_iter=1)引数のmax_iterには一度に出力する候補点の数を設定します。
今回は候補点を一つずつ確認したかったのでmax_iterは1で設定しています。
学習モデルの可視化
最後に学習モデルの可視化について解説します。
今回のコードでは以下の部分でガウス過程回帰及び獲得関数を可視化するように実行しています。
bo.plot_acquisition()#ガウス過程回帰のプロットと獲得関数のグラフを表示これにより以下の様にガウス過程回帰と獲得関数を可視化することができます。
可視化した画像を保存したい場合はplot_acquisition()の引数にXXXX.jpegのようにファイル名+拡張子を設定します。
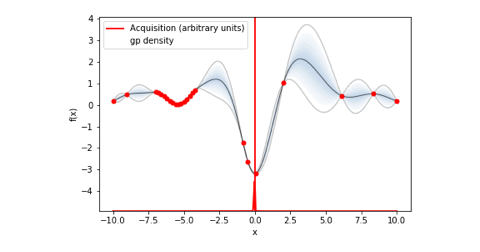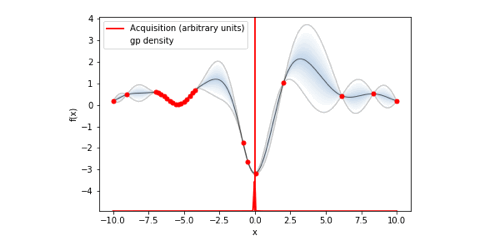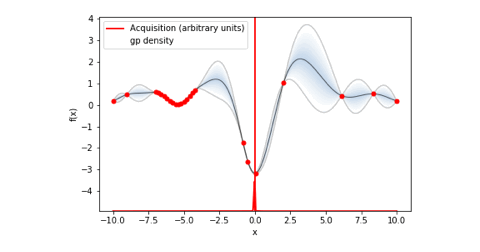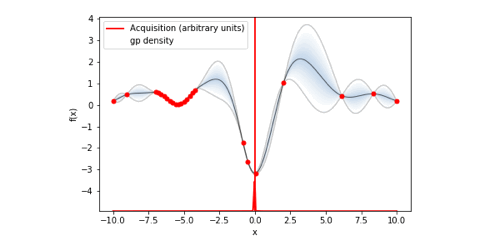

ちなみに今回は特に可視化はしませんでしたが、以下のコードを実行すると目的変数の収束状況のプロットを可視化することもできます。
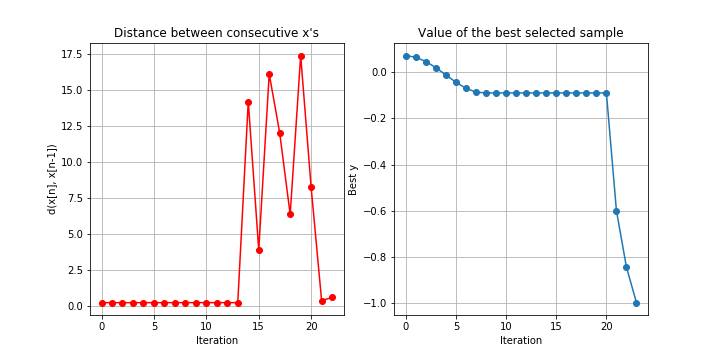
bo.plot_convergence()実際は以下の様なグラフが出力されます。
こちらも引数にファイル名+拡張子を設定することで画像を保存することができます。

終わりに
以上が簡単ですが、GPyOptでベイズ最適化を実行する方法についての解説になります。GPyOptには今回解説したしたメソッド以外にもたくさんのメソッドがありますので、今後紹介できればと思います。