こんにちは!ぼりたそです!
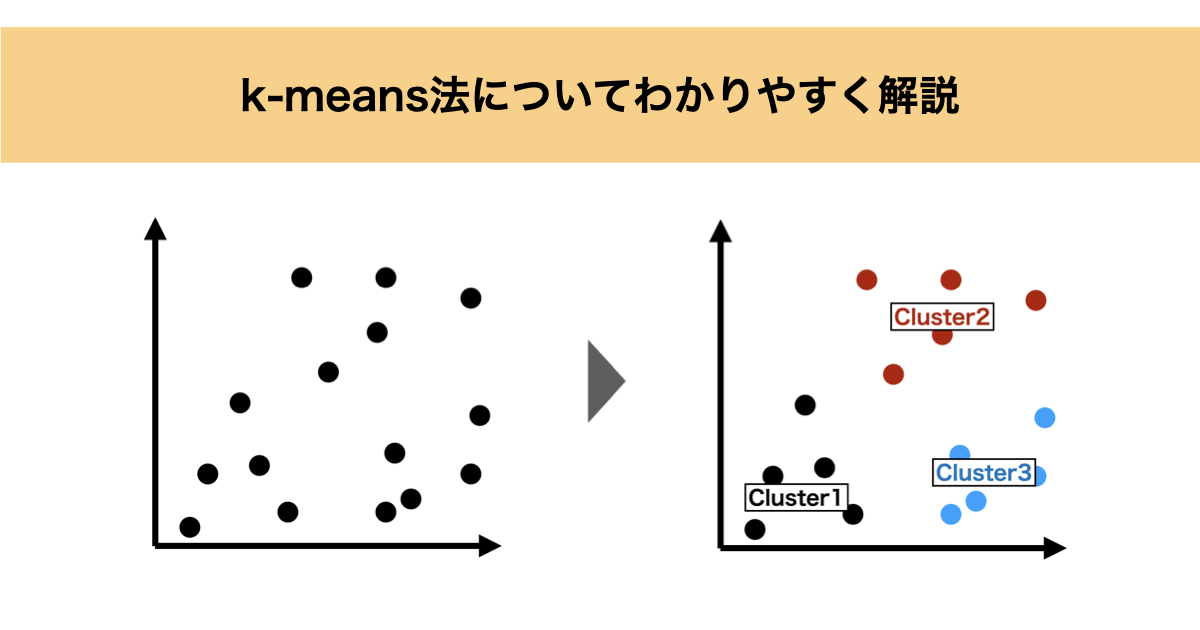
今回はクラスタリング手法であるk-means法についてわかりやすく解説していきます。
k-means法は、教師なし学習の代表的なアルゴリズムであり、「データを似たもの同士で自動的にグループ分けする」ために使われます。
本記事では、
- k-means法とは何か
- どんな特徴があるのか
- アルゴリズムについて
- Pythonにおける実装
を 初学者でもイメージできるように 解説します。
k-means法とは?
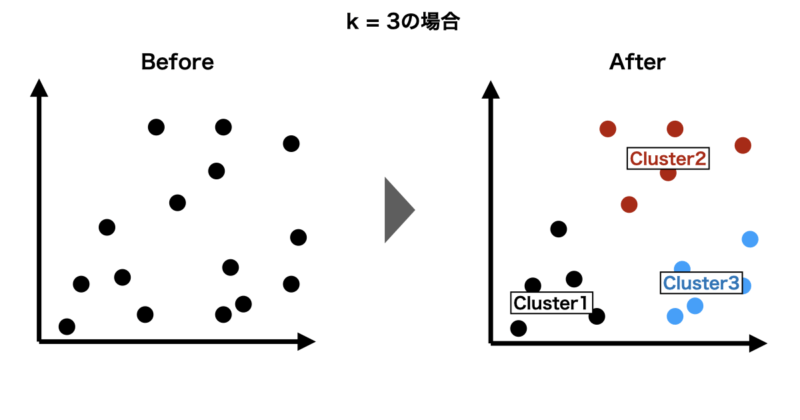
k-means法とは、データをあらかじめ指定した k 個のグループ(クラスタ)に分割する手法です。
最大の特徴は、
- 正解ラベルを必要としない(教師なし学習)
- データ同士の「距離」をもとに分類する
という点です。
例えば、
- 顧客データを購買傾向ごとに分けたい
- 材料データを性質の近いグループに分けたい
- 大量のデータの全体構造を把握したい
といった場面でよく使われます。
k-means法の特徴とメリット・デメリット
次k-means法のメリット、デメリットについて説明していきます。
k-means法のメリット
① アルゴリズムがシンプルで理解しやすい
k-means法は「割り当て」と「平均」の繰り返しという非常に単純な構造です。
② 計算が高速
計算量が比較的少ないため、大規模データにも適用しやすい特徴があります。
③ 結果の解釈がしやすい
各クラスタには「中心(重心)」が存在するため、「このグループはどんな特徴か?」を説明しやすいです。
k-means法のデメリット
① クラスタ数 k を事前に決める必要がある
kの正解は分からないため、試行錯誤が必要です。
② 球状のクラスタが前提
細長い分布や複雑な形状のクラスタはうまく分けられません。
③ 初期値に依存する
初期のクラスタ中心の置き方によって、結果が変わることがあります。
k-means法のアルゴリズム
k-means法は、
「似ているデータを自然に集めたい」
という直感的な目的を、とても簡単な方法で実現しています。
ここでは、
- 実際に何を繰り返しているのか
- なぜその操作でクラスタができるのか
を説明します。
k-means法がやろうとしていること
k-means法の目的は、とてもシンプルです。
同じグループに入ったデータ同士は、なるべく近くに集めたい
これを言い換えると、
- 各グループに「代表点(中心)」を置き
- 各データは、その代表点にできるだけ近づける
という考え方になります。
ステップ1:クラスタ中心をとりあえず置く
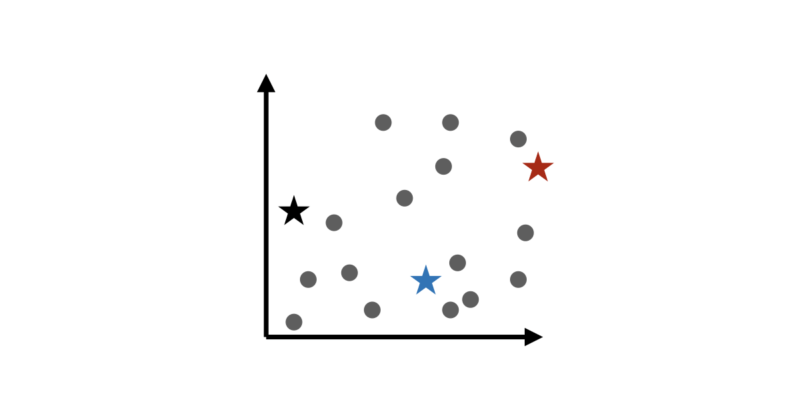
最初に、k個のクラスタ中心を 適当に配置します。
このクラスタ中心については、
- まだ意味のある中心ではない
- 「スタート地点を決める」だけ
であり、このステップできちんとクラスタ中心を求める必要はありません。
k-means法は あとから何度も修正する前提のアルゴリズムです。
ステップ2:近い中心にデータをラベリングする
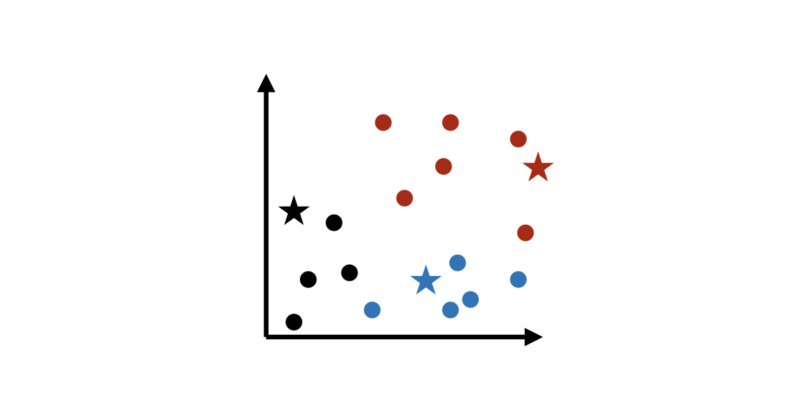
次に、各データ点について考えます。
「このデータは、どの中心に一番近いか?」
このルールに従ってデータをラベリングすると、自然といくつかのグループに分かれます。
ここで使われているのは、
距離が近い=似ている
という直感的なルールです。
ステップ3:クラスタ中心を“平均”の位置に動かす
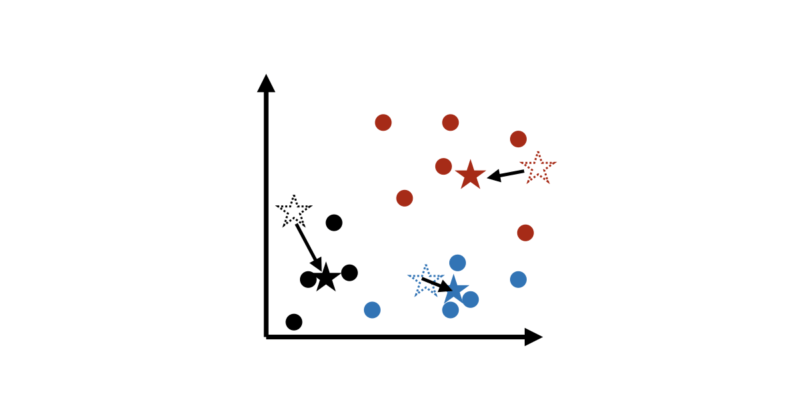
データが集まったら、次にやることは簡単であり、そのグループに属するデータの重心(平均)の位置にクラスタ中心を移動させます。
この「平均を取る」という操作が
k-means の “means” の由来です。
ステップ2、3を繰り返す
k-means法は、実は次の2つしかやっていません。
- 近い中心にデータを集める
- データの平均位置に中心を動かす
これを何度も繰り返すと、中心の移動はだんだん小さくなり最終的にほとんど動かなくなります
その時点で、「これ以上きれいには分けられない」という状態に到達します。
アルゴリズムとしては非常にシンプルでかつ確実にクラスタリングできる手法となりますが、万能ではありません。
例えば、
- 最初の中心の置き方で結果が変わる
- 丸い形のグループが前提
- 複雑な分布は苦手
という特徴もあります。そのため、kの決め方やデータの標準化が重要になります。
Pythonでの実装
ここでは、k-means法の動作を直感的に理解することを目的として、
次のようなシンプルなクラスタリング問題を考えます。
- 特徴量は 2変数(2次元)
- データ数は 約100個
- データは 3つの塊(クラスタ) を持つように人工的に生成
- クラスタ数は k = 3
教師なし学習である k-means法では、
「正解ラベル」は一切与えられません。
そのため本問題では、
データの分布だけを手がかりに、
k-means法がどのようにクラスタを形成していくのか
を見ていきたいと思います。
実際に使用するコードは以下に示すとおりです。
import numpy as np
import matplotlib.pyplot as plt
# =========================
# 1) 2変数・3クラスタのデータ作成(約100点)
# =========================
def make_2d_3cluster_data(n_total=100, seed=42):
rng = np.random.default_rng(seed)
# だいたい均等に(100点前後)
n1 = n_total // 3
n2 = n_total // 3
n3 = n_total - n1 - n2
# 3つのクラスターをガウス分布で作る(位置は適度に離す)
c1 = rng.normal(loc=[0.0, 0.0], scale=[0.6, 0.6], size=(n1, 2))
c2 = rng.normal(loc=[4.0, 0.5], scale=[0.7, 0.5], size=(n2, 2))
c3 = rng.normal(loc=[2.0, 4.0], scale=[0.5, 0.7], size=(n3, 2))
X = np.vstack([c1, c2, c3])
rng.shuffle(X)
return X
# =========================
# 2) k-meansの実装(イテレーションごとに中心を保存)
# =========================
def kmeans_manual_with_history(X, k=3, max_iter=10, seed=0):
rng = np.random.default_rng(seed)
# 初期重心:データ点からランダムにk個選ぶ
init_idx = rng.choice(len(X), size=k, replace=False)
centroids = X[init_idx].copy()
history = [] # 各反復の (centroids, labels, inertia) を保存
for it in range(max_iter):
# --- Assignment(割り当て) ---
# 距離の二乗(N x k)
d2 = np.sum((X[:, None, :] - centroids[None, :, :]) ** 2, axis=2)
labels = np.argmin(d2, axis=1)
# inertia(クラスタ内距離二乗和:SSE)
inertia = 0.0
for j in range(k):
pts = X[labels == j]
if len(pts) > 0:
inertia += np.sum((pts - centroids[j]) ** 2)
# 履歴に保存(更新前のcentroidsとlabelsでもOKだが、ここでは更新後を見たいので一旦保存用にコピー)
history.append((centroids.copy(), labels.copy(), float(inertia)))
# --- Update(重心更新) ---
new_centroids = centroids.copy()
for j in range(k):
pts = X[labels == j]
if len(pts) == 0:
# 空クラスタ対策:ランダムな点で再初期化
new_centroids[j] = X[rng.integers(0, len(X))]
else:
new_centroids[j] = pts.mean(axis=0)
# 収束判定(中心の移動がほぼゼロなら終了)
if np.allclose(new_centroids, centroids, atol=1e-6):
centroids = new_centroids
# 収束後の状態も追加で入れておく
d2 = np.sum((X[:, None, :] - centroids[None, :, :]) ** 2, axis=2)
labels = np.argmin(d2, axis=1)
inertia = 0.0
for j in range(k):
pts = X[labels == j]
if len(pts) > 0:
inertia += np.sum((pts - centroids[j]) ** 2)
history.append((centroids.copy(), labels.copy(), float(inertia)))
break
centroids = new_centroids
return history
# =========================
# 3) イテレーションごとの可視化
# =========================
def plot_kmeans_history(X, history, k=3):
# 軸範囲を固定(イテレーションでグラフがブレないように)
x_min, x_max = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
y_min, y_max = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0
for it, (centroids, labels, inertia) in enumerate(history):
plt.figure(figsize=(6, 5))
# クラスタごとに散布(色はmatplotlibのデフォルトサイクルに任せる)
for j in range(k):
pts = X[labels == j]
plt.scatter(pts[:, 0], pts[:, 1], alpha=0.8, label=f"Cluster {j}")
# 重心(markerだけ変える。色は指定しない)
plt.scatter(centroids[:, 0], centroids[:, 1], marker="X", s=250, label="Centroids")
# 重心にラベルを付ける
for j in range(k):
plt.text(centroids[j, 0], centroids[j, 1], f" C{j}", fontsize=10)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title(f"k-means iteration {it} (SSE={inertia:.2f})")
plt.legend()
plt.tight_layout()
plt.show()
# =========================
# 実行
# =========================
X = make_2d_3cluster_data(n_total=100, seed=42)
history = kmeans_manual_with_history(X, k=3, max_iter=10, seed=0)
plot_kmeans_history(X, history, k=3)
それでは出力された結果について解説していきます。
◼️ Iteration0(初期状態)
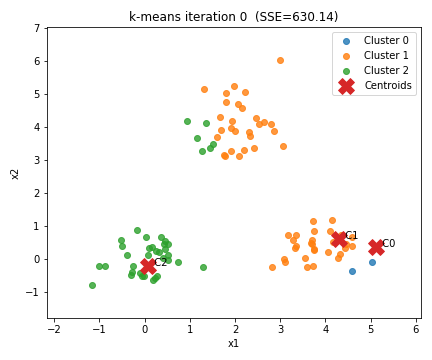
最初のイテレーションでは、
クラスタ中心(重心)は ランダムな位置 に配置されています。
この時点では、
- 重心はデータの中心とはズレている
- クラスタの割り当てもまだ不安定
という状態です。
そのため、
一見するときれいに分かれていないように見えます。
◼️ Iteration1-3
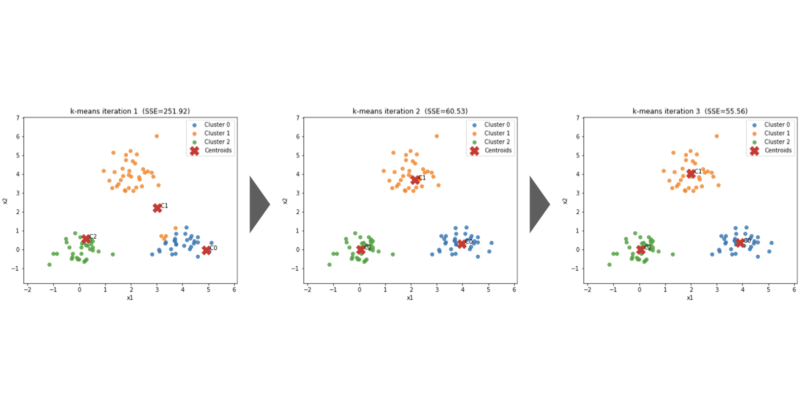
イテレーションを1回進めるごとに、
以下の2つの操作が繰り返されます。
- 各データ点を、最も近い重心に割り当てる
- 各クラスタに属するデータの平均位置に重心を移動する
これにより、重心はデータの密集している方向へ移動しクラスタ内のばらつきが徐々に小さくなっていきます。
グラフを見ると、重心(×印)が少しずつデータの中心に近づいていく様子やクラスタの境界が安定していく様子が確認できるはずです。
◼️ Iteration3 (収束状態)
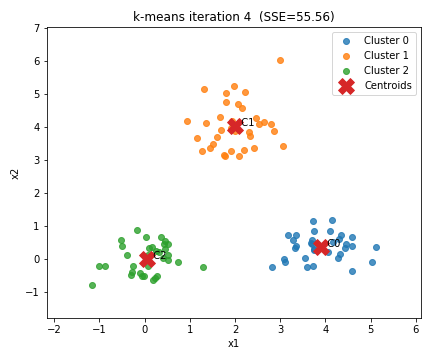
最終的には、重心の位置がほとんど変わらなくなりクラスタの割り当ても固定されます。
この状態が、k-means法における 収束 です。
タイトルに表示している SSE(クラスタ内距離の二乗和)もイテレーションが進むにつれて減少し、最終的にほぼ変化しなくなります。
これは、クラスタ内のデータが、できるだけ重心の近くに集まったことを意味します。
まとめ
- k-means法は 教師なし学習の代表的クラスタリング手法
- 「距離」と「平均」を使ってデータを分割する
- シンプル・高速・分かりやすいが万能ではない
- kの決め方や前処理(標準化)が重要
k-means法は、クラスタリングの 最初の一歩として最適なアルゴリズム です。
この手法を理解しておくことで、他の高度なクラスタリング手法への理解もスムーズになります。