こんにちは!ぼりたそです!
機械学習を学び始めると、まず登場するアルゴリズムのひとつが k近傍法(k-Nearest Neighbors, kNN) です。
本記事では、
- k近傍法の考え方
- アルゴリズムの流れ
- メリット・デメリット
- Pythonによる実装と可視化
までを、わかりやすく解説します。
k近傍法の考え方
k近傍法は、次のようなとてもシンプルな考え方に基づいています。
「近くにあるデータ同士は、似た性質を持つはず」
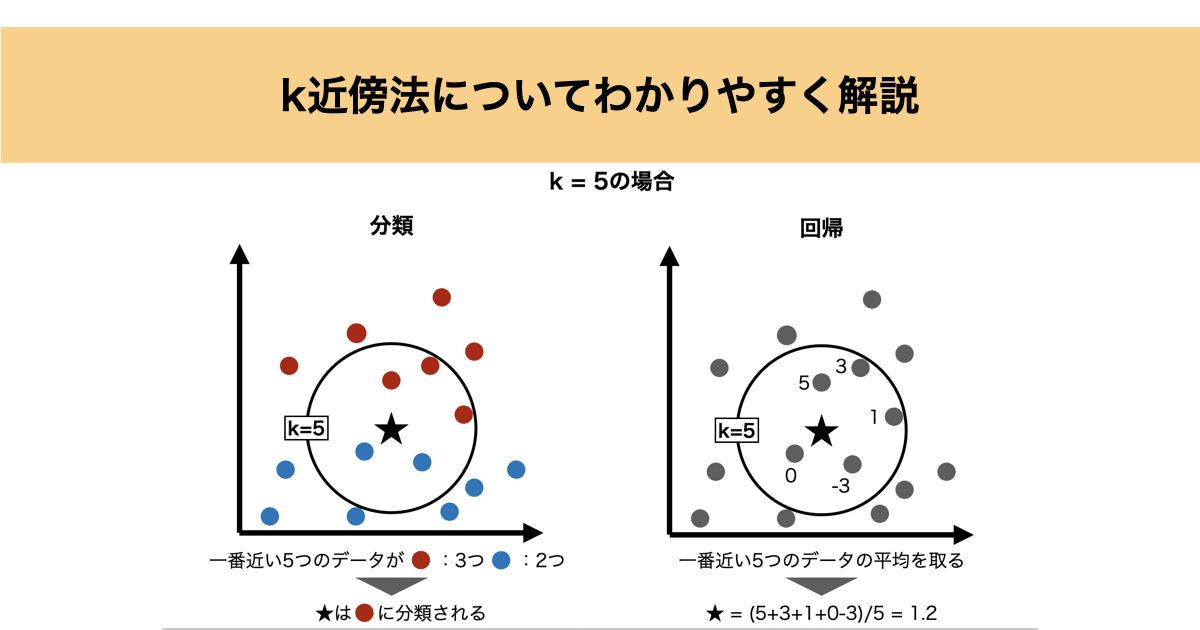
この考え方から、予測したいデータの周囲にある k個の近いデータ(近傍) を調べ、その情報を使って予測を行います。
k近傍法のアルゴリズム
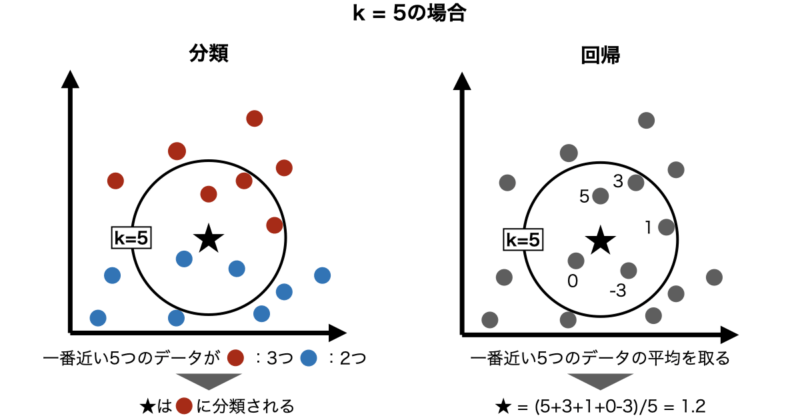
k近傍法の手順は次の3ステップだけです。
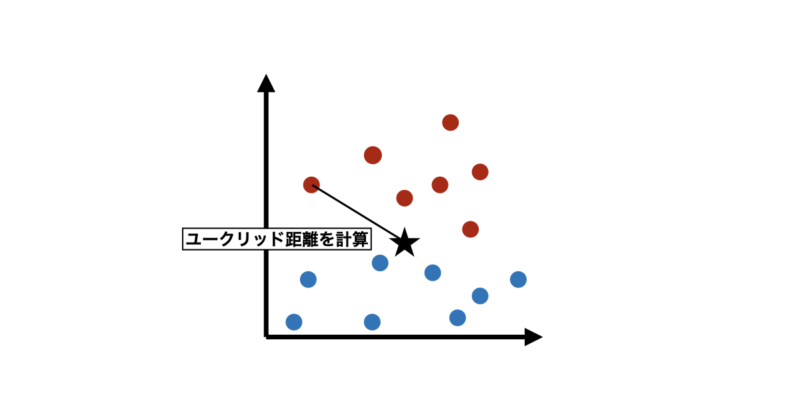
ステップ① 距離を計算する
予測したい点と、すべての学習データとの距離を計算します。
最もよく使われるのは ユークリッド距離 です。
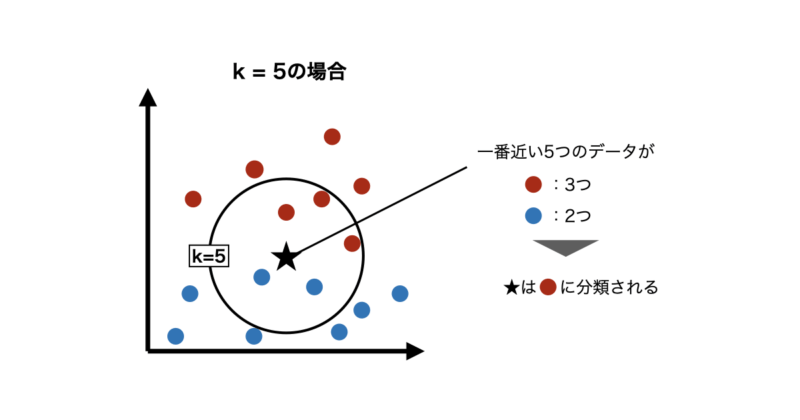
ステップ② 近い順にk個選ぶ
距離が小さい順に並べ、上位 k個 を取り出します。
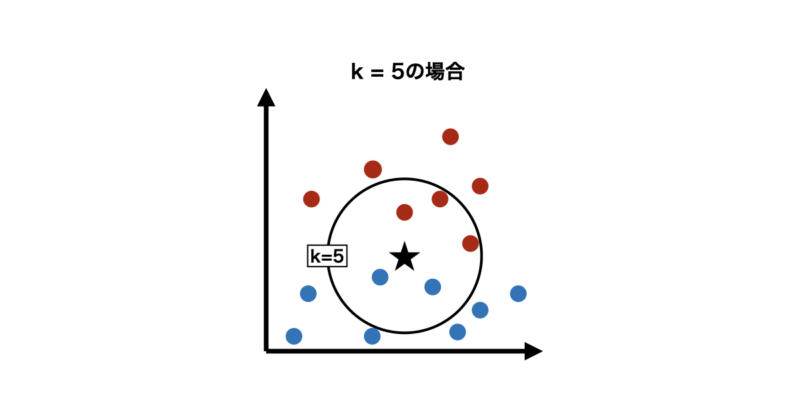
ステップ③ 予測を決定する
- 分類:多数決
- 回帰:平均値
にて予測値を算出します。
k近傍法のメリット・デメリット
次にk近傍法のメリット・デメリットについて解説します。
◼️メリット
- 直感的で理解しやすい
→「距離が近い=似ている」という発想は直観的に理解しやすいです。
- 学習がほぼ不要
→事前にモデルを学習する必要がなく、データを保存しておくだけで利用できます。
- 非線形な境界を表現できる
→線形モデルでは表現できない、複雑な分類境界にも自然に対応できます。
◼️デメリット
- 予測時の計算コストが高い
→新しいデータが蓄積される度に「全データとの距離計算」が必要になります。データ数・次元数が増えると、実用上厳しくなります。
- 次元の呪いに弱い
→特徴量が多くなると、距離の差が分かりにくくなり、k近傍法の性能が落ちやすくなります。
- kの選び方が難しい
kが小さい → ノイズに弱く過学習
kが大きい → ぼやけて精度低下
実際に使用する場合、 交差検証でkを決める のが一般的です。
Pythonで実装
ここからは、k近傍法を Pythonで動かしながら理解 していきます。
いきなり実装に入る前に、今回使うデータの意味を押さえましょう。
今回使うデータ
今回は scikit-learn の make_classification を使い、2次元の分類データ(100点) を人工的に作ります。
このデータは、ざっくり言うと次のようなものです。
- 特徴量(X):2つ
- Feature 1(横軸)
- Feature 2(縦軸)
- 目的変数(y):クラスラベル(0 or 1)
- 0:クラスA
- 1:クラスB
散布図で見ると「赤い点のグループ」と「青い点のグループ」があり、k近傍法で「新しい点はどちらのグループか?」を判定する境界線を定義することが目的です。
データを作って可視化する
まずはデータ作成と散布図の表示です。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
# ===== ベースデータ生成 =====
X, y = make_classification(
n_samples=200,
n_features=2,
n_redundant=0,
n_informative=2,
n_clusters_per_class=1,
class_sep=1.0,
random_state=42
)
# 線形変換行列(斜めに引き伸ばす)
A = np.array([[0.8, -0.6],
[0.4, 1.2]])
X = X @ A # データを斜め方向に変換
# 可視化
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm", edgecolor="k")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Anisotropic (Skewed) Clusters")
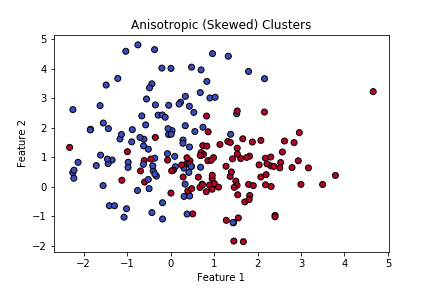
plt.show()出力される散布図は以下の通りで、2つの正解ラベルがそれぞれクラスターを形成していますが、互いのクラスターが重なり合う部分があるため、分類が難しい状況を想定しています。

k近傍法で分類する
次に k近傍法を適用します。
今回は k=5(近い点を5個見る)としてみます。
from sklearn.neighbors import KNeighborsClassifier
# k近傍法(k=5)
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X, y)
k近傍法は「学習」というより、
データを保存しておいて予測時に参照する手法なので、fitは一瞬で終わります。
分類境界の図示
次に目的である「分類境界」の可視化を実行してみましょう。
手法としては、特徴量の二次元空間に大量の点を用意し、それぞれをk近傍法により分類させ背景色を分けることで分類の境界線が一目でわかります。
# グリッド作成(平面を細かい点で埋める)
xx, yy = np.meshgrid(
np.linspace(X[:, 0].min()-1, X[:, 0].max()+1, 200),
np.linspace(X[:, 1].min()-1, X[:, 1].max()+1, 200)
)
# 各グリッド点を分類
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 分類境界の描画
plt.contourf(xx, yy, Z, alpha=0.3, cmap="coolwarm")
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm", edgecolor="k")
plt.title("k-NN Decision Boundary (k=5)")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
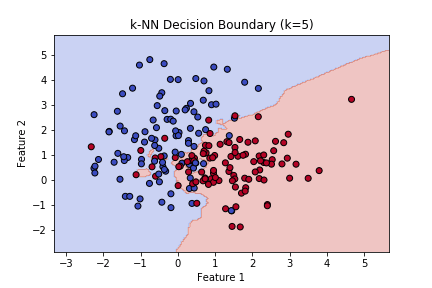
出力される散布図は以下の通りで、二次元空間上のどの点にデータが追加されても、どちらのクラスに分類されるかがわかるかと思います。
kを変えると境界はどう変わる?
では次にk近傍法のハイパーパラメータである kの値について変化させてみましょう。
ks = [1, 5, 15]
for k in ks:
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X, y)
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3, cmap="coolwarm")
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm", edgecolor="k")
plt.title(f"k-NN Decision Boundary (k={k})")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
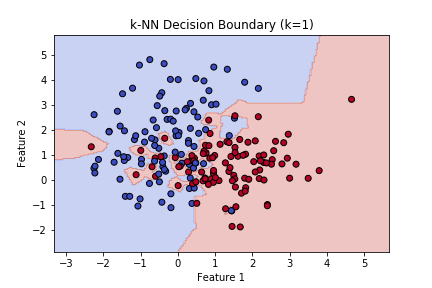
- k = 1の場合
→ 近くの1点だけで決めるので、境界がギザギザで過学習気味
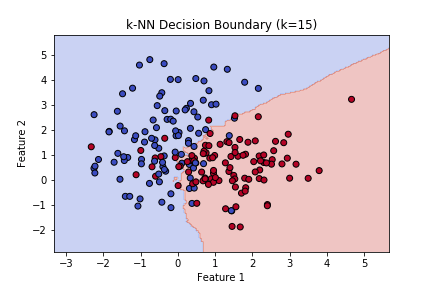
- k = 15の場合
→ 多数の点で平均化され、境界がなめらかになっていることがわかります。
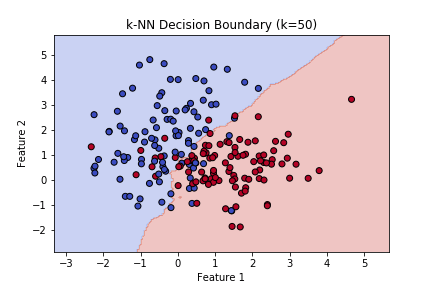
- k = 50の場合
→ 非常に多くの点で平均化されているため境界がざっくりし過ぎており、精度は低いように思えます。
このようにkの値によりかなり精度が変わってくるので、交差検証などを用いて評価することで最適なkを見つ蹴るのが好ましいです。
まとめ
本記事では、k近傍法(k-NN)の基本的な考え方からアルゴリズム、Pythonによる実装と可視化までを解説しました。
k近傍法は「近いデータ同士は似ている」という直感的な発想に基づくシンプルな手法で、機械学習の基礎を理解するのに適しています。一方で、kの値によって挙動が大きく変わる点や、データ数が増えると計算コストが高くなる点には注意が必要です。
可視化を通して、kを変えることで分類境界がどのように変化するかを確認できたことで、k近傍法の特徴を直感的に理解できたのではないでしょうか。