こんにちは!ぼりたそです!
今回は、ガウス過程回帰(GPR)などで使われるカーネル関数のハイパーパラメータをどうやって決めるのか?というテーマについて掘り下げてみます。
一般的には、最尤推定(Maximum Likelihood Estimation, MLE)と呼ばれる方法が使用されており、数式・仕組み・Pythonでの実装までわかりやすく紹介していきます。。
この記事は以下のポイントでまとめています
- カーネル関数とは?
- カーネル関数のハイパーパラメータ
- 最尤推定の考え方
- ガウス過程回帰における最尤推定
- Pythonでの実装
それでは詳細に解説していきます。
カーネル関数とは?
まず、ハイパーパラメータについて説明する前にカーネルについて簡単に説明します。
ガウス過程回帰やサポートベクターなどでカーネル関数を使用すると思いますが、このカーネル関数とはデータ同士がどれだけ似ているかを評価する指標です。
例えば、トランプ52枚があったとして、それを似ているもの同士で分類して下さいと言われたらあなたはどのようにして分類しますか?
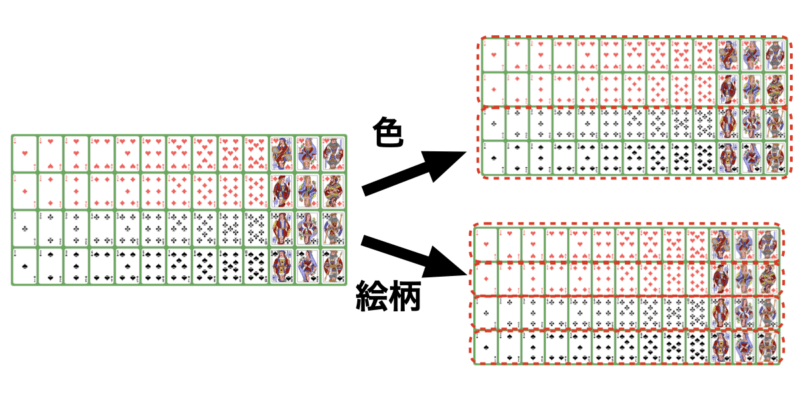
それはトランプの「色」かもしれませんし、「マーク」や「数字」、「絵柄」かもしれません。
この分類する際に指標としている「色」や「マーク」がガウス過程回帰などではカーネル関数という考え方になります。
カーネル関数について詳しく知りたい方は以前まとめた記事がありますので、参考にしていただければと思います。
カーネル関数のハイパーパラメータ
それではカーネルにおけるハイパーパラメータとは何かを説明していきます。
カーネルのハイパーパラメータとは先ほどご紹介したカーネル関数に登場するパラメータであり、「調節ねじ」のようなものとご理解ください
カーネルの説明の際にトランプの分類の例を挙げたと思います。トランプを分類する指標をカーネルとすると、指標の範囲を決めるのがハイパーパラメータになります。
例えば、52枚のトランプを分類する際に「数字」と言う指標で分類するとしましょう。しかし、数字と言っても意味が広すぎますね。
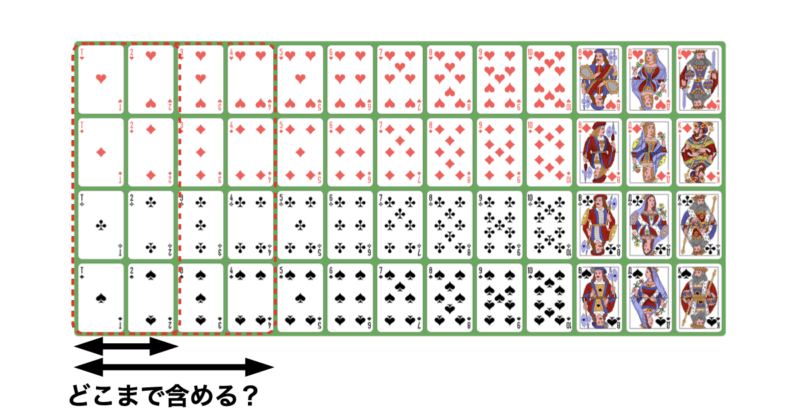

AからKまで同じ数字同士でまとめましょうか?それとも隣り合っている数字(「1,2」、「2,3」)は似ているとしてまとめましょうか?はたまた一桁と二桁の数字でまとめましょうか?
「数字」の指標の中でもどこまで類似しているかを線引きするのがハイパーパラメータの役割と言えます。
ガウス過程回帰でよく使用されるカーネル関数としてRBF(ガウシアンカーネル)があります。
関数は以下のような数式になっています。
$$K(x, x’) = \exp\left(-\frac{|x – x’|^2}{2\ell^2}\right) $$
RBFカーネルはデータ間の類似性を評価する際に、どれだけ遠いデータを類似とみなすかを調整します。
ハイパーパラメータは $\ell$ であり、$\ell$ が大きい場合、広い範囲のデータを類似とみなします。逆に$\ell$ が小さい場合、近いデータのみを類似とみなします。
このようにRBFカーネルに関してはハイパーパラメータ $\ell$ によってどの範囲までデータが類似しているかを線引きしているわけですね。
最尤推定とは?
最尤推定(MLE)は、「観測されたデータが最も起こりやすくなるようにハイパーパラメータを選ぶ」方法です。
要するに、「今あるデータを一番うまく説明できるようなカーネル関数のパラメータを探そう!」という考え方ですね。
GPRでは尤度関数(Likelihood)が解析的に書け、その勾配も計算可能なので効率的に最適化できます。
最尤推定については以下の記事で詳しく解説していますので、ご参考にしていただければと思います。
GPRにおける最尤推定
一般的な回帰モデルでは、パラメータ(回帰係数など)を調整して尤度を最大化しますが、GPRでは少し異なります。
なぜなら、GPRでは、予測関数 $f(x)$ そのものが確率的な存在(分布)として扱われます。つまり、$f(x)$ の形が1つに決まっていないのです。
そのため、観測データ $\mathbf{y}$ の尤度を求めるには、
$$p(\mathbf{y} \mid \theta) = \int p(\mathbf{y} \mid \mathbf{f(x)}) \cdot p(\mathbf{f(x)} \mid \theta) \, d\mathbf{f(x)}$$
$\theta$ = ハイパーパラメータ
のように、関数 $f(x)$ に対して積分を行うことで確率を「平均」して評価する必要があります。
この操作(積分)を「周辺化(marginalization)」と呼び、
得られる尤度を「周辺尤度(Marginal Likelihood)」と言います。
周辺化した関数は以下のような数式となります。
$$p(\mathbf{y} \mid \theta) = \frac{1}{(2\pi)^{n/2} \, |K + \sigma_n^2 I|^{1/2}} \exp\left( -\frac{1}{2} \mathbf{y}^\top (K + \sigma_n^2 I)^{-1} \mathbf{y} \right)$$
$K$:カーネル行列($K_{ij} = k(x_i, x_j)$)。$n \times n$ の対称行列。
$\sigma_n^2$:観測ノイズの分散。
$I$:$n \times n$の単位行列。
このままでは解析的に解けないため、対数をとり対数周辺尤度に変形します。
$$\log p(\mathbf{y} \mid \theta)
= -\frac{1}{2} \mathbf{y}^\top (K + \sigma_n^2 I)^{-1} \mathbf{y}\frac{1}{2} \log |K + \sigma_n^2 I|\frac{n}{2} \log 2\pi$$
この関数を最大化することで、「一番もっともらしいハイパーパラメータ $\theta$」が得られます。そして、関数の最大化にはL-BFGS-B法を用います。
L-BFGS-B法は、関数の最小値を見つけるための反復的な最適化手法です。
具体的には、関数の勾配(傾き)を利用して、関数の値が小さくなる方向にパラメータを少しずつ更新していきます。
わかりやすく例えるなら、山の頂上から谷底へと降りていくようなイメージです。地形の傾きを調べて「この方向に進めば下れる」と判断しながら、一歩一歩慎重に谷底を目指して進んでいく——この動作を何度も繰り返すことで、最終的に関数の最小値にたどり着きます。
ただし、ガウス過程回帰で最適化したいのは対数周辺尤度(log marginal likelihood)であり、これは最大化するべき関数です。
L-BFGS-B法は「最小化」アルゴリズムなので、対数周辺尤度にマイナス符号(-1)をかけて、最大化問題を最小化問題に変換してから適用します。
このようにして、L-BFGS-B法はカーネル関数のハイパーパラメータを少しずつ更新しながら、対数周辺尤度を最大にするパラメータを探していきます。最終的に収束すれば、それが最尤推定による最適化が完了した合図です。
以上がガウス過程回帰における最尤推定になります。
Pythonで実行
では、実際にPythonコードで最尤推定を実行してハイパーパラメータを最適化してみましょう。
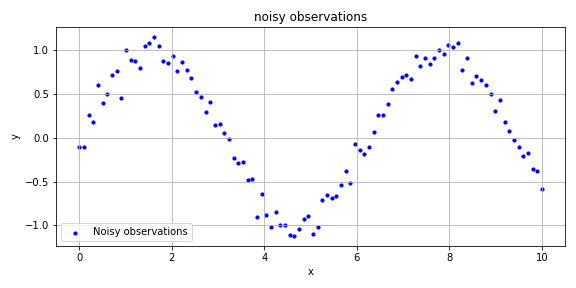
用意した仮想データは以下の通りとなります。sin関数にノイズを加えたデータが元になっており、青いプロットに対してガウス過程回帰を実行します。
$X$:0〜10の範囲を100分割した1次元データ
$y$:sin波にノイズを加えたデータ

今回は以下に示すRBF Kernel+WhiteKernelを使用してハイパーパラメータである$ \ell $(RBFのスケール長), $ \sigma_n $(WhiteKernelのノイズレベル)に対して最尤推定を実行します。
$$K(x, x’) = \underbrace{\exp\left( -\frac{(x – x’)^2}{2\ell^2} \right)}_{\text{RBF kernel}} + \underbrace{\sigma_n^2 \delta(x – x’)}_{\text{WhiteKernel}}$$
実行に用いたPythonコードは以下の通りです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
from scipy.optimize import minimize
# データの準備
X = np.atleast_2d(np.linspace(0, 10, 100)).T
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# 初期カーネル(ハイパーパラメータ初期値)
kernel = RBF(length_scale=1.0) + WhiteKernel(noise_level=1.0)
gpr = GaussianProcessRegressor(kernel=kernel, optimizer=None)
# トラジェクトリ記録用リスト
trajectory = []
# 目的関数:負の対数周辺尤度
def objective(theta):
trajectory.append(theta.copy()) # ログスケールで記録
kernel_ = gpr.kernel.clone_with_theta(theta)
gpr_temp = GaussianProcessRegressor(kernel=kernel_, optimizer=None)
gpr_temp.fit(X, y)
return -gpr_temp.log_marginal_likelihood(theta)
# 最適化の実行
res = minimize(objective, gpr.kernel.theta, method='L-BFGS-B')
# トラジェクトリをlog → 線形スケールに戻す
trajectory = np.array(trajectory)
length_scales = np.exp(trajectory[:, 0])
noise_levels = np.exp(trajectory[:, 1])
# データフレームに変換
df_trajectory = pd.DataFrame({
"iteration": np.arange(len(trajectory)),
"length_scale (RBF)": length_scales,
"noise_level (WhiteKernel)": noise_levels
})
# 表示(オプション:print(df_trajectory.head()) などで中身確認)
print(df_trajectory)
# 可視化(オプション)
plt.plot(length_scales, label="length_scale (RBF)")
plt.plot(noise_levels, label="noise_level (WhiteKernel)")
plt.xlabel("Iteration")
plt.ylabel("Hyperparameter value")
plt.legend()
plt.title("Hyperparameter Optimization Trajectory")
plt.grid()
plt.tight_layout()
plt.show()
以下に上記コードを実行した際のハイパーパラメータのトラジェクトリ(軌跡)をグラフで示します。
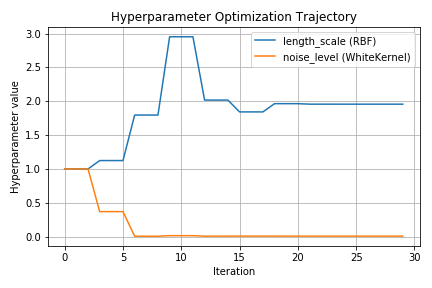

いずれのハイパーパラメータも初期値を1として最尤推定を実行していますが、Iteration(パラメータ更新)を経るごとに徐々に収束していることがわかります。
このようにガウス過程回帰では最尤推定を用いることで自動的にカーネルのハイパーパラメータを最適化してくれます。
まとめ
以上がGPRにおけるカーネル関数のハイパーパラメータ最適化の解説になります。数学的に理解が難しいところもありますが、ハイパーパラメータの最適化についてなんとなくの流れや仕組みについて理解の一助になれば幸いです。