Lasso & Ridge回帰についてわかりやすく説明

こんにちは！ぼりたそです！

今回は「Lasso回帰とRidge回帰」について、初学者にも分かりやすく解説していきます。

どちらも線形回帰の一種で、特に過学習（オーバーフィッティング）を防ぐための手法としてよく使われます。データ分析や機械学習を行う上では避けて通れない重要な回帰手法なので、ぜひ押さえておきたいところです！

この記事は以下のポイントでまとめています。

Point

過学習について
　
正則化について
　
Lasso & Ridge回帰について
　
回帰性能についてPythonで比較

また、学習データとしてCSVファイルを入力するだけでLasso、Ridge回帰を実行するPythonコードも紹介していますので、ご興味ある方は以下の記事を参照ください。

合わせて読みたい

それでは順に解説していきます。

過学習について
正則化とLasso & Ridge回帰
Lasso & Ridge回帰
Lasso & Ridge回帰をPythonで比較
終わりに

過学習について

まずは「過学習」について説明しましょう。

過学習とは、モデルが学習データには非常によく当てはまっているのに、未知のデータに対して予測精度が下がってしまう現象です。

モデルが“学習しすぎて”しまって、ノイズまで覚えてしまうことで起きます。

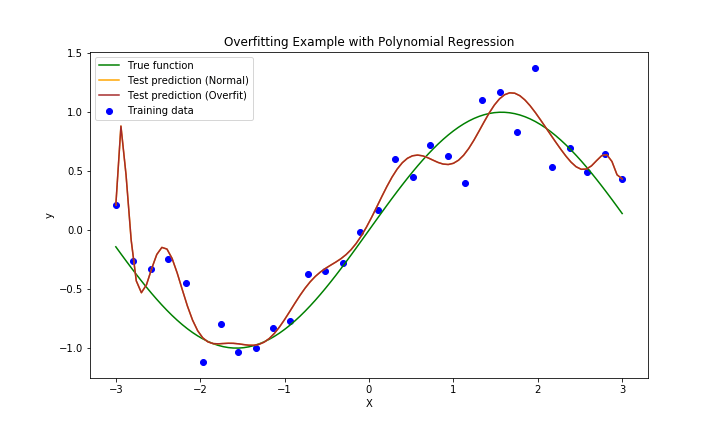
下に線形回帰時に過学習した例を示します。

緑線：真の関数（正解）
赤線：学習済みのモデル
青点：学習データ

赤線は学習データにピッタリすぎており、不自然に波打っているのがわかります。これがまさに過学習の典型例です。

真の関数と比較すると歪になっており、これだと予測の精度が下がってしまうのもわかるかと思います。

では、どうすれば過学習を防げるのでしょうか？

その答えの一つが「正則化」です。

正則化とLasso & Ridge回帰

では、正則化がどのようなものか説明していきます。

正則化は過学習を防ぐ手法の一つであり、モデルの複雑さを制御することで汎化性能を向上させます。

まず、通常の線形回帰分析では変数の係数を決める際に最小二乗法を使用しているかと思います。

最小二乗法とは関数が$y = a_1x_1 + a_2x_2 + \ldots + a_nx_n$ ($a_i$は変数の係数)であるときに以下の損失関数が最小となるように変数の係数を決定する手法です。

■最小二乗法

$$\sum_{i=1}^{N} \left( y_i – \sum_{j=1}^{n} a_j x_{ij} \right)^2$$

しかし、この最小二乗法では過学習に陥ることがあり、その場合、係数 $a_i$ が極端に大きくなる場合があります。

この過学習を防ぐために正則化項を導入します。

正則化は大きく2種類ありL1正則化、L2正則化項が存在します。

それぞれ以下の式で表されます。

■L1正則化項

$$| \mathbf{a} |_1 =\lambda \sum_{i=1}^{n} |a_i|$$
→ 一部の係数を完全にゼロにする（特徴量選択が可能）

■L2正則化項

$$| \mathbf{a} |_2 = \lambda \sum_{i=1}^{n} a_i^2$$
→ 全ての係数を少しずつ小さくする（滑らかに抑える）

L1正則化項は係数の絶対値の和の項になっており、L2は係数の二乗和の項になっています。

先ほど説明した最小二乗法に正則化項を組み込んだ損失関数を使用して係数決定する手法がLasso回帰やRidge回帰になるのです。

詳しくは次の章でご説明します。

Lasso & Ridge回帰

では、LassoとRidgeの具体的な損失関数と、それぞれの特徴を見てみましょう。

■Lasso回帰（最小二乗法＋L1正則化項）

$$\sum_{i=1}^{N} \left( y_i – \sum_{j=1}^{n} a_j x_{ij} \right)^2 + \lambda \sum_{j=1}^{n} |a_j|$$

Lasso回帰は最小二乗法にL1正則化項を組み込んで係数を決定する手法であり、L1正則化項によって係数の絶対値の和にペナルティを課すため、不要な特徴量の係数をゼロにする傾向があります。そのため、特徴量の選択が重要な場合や、モデルの解釈性を高めたい場合に適しています。

■Ridge回帰（最小二乗法＋L2正則化項）

$$\sum_{i=1}^{N} \left( y_i – \sum_{j=1}^{n} a_j x_{ij} \right)^2 + \lambda \sum_{j=1}^{n} a_j^2$$

Ridge回帰は最小二乗法にL2正則化項を組み込んで係数を決定する手法であり、L2正則化項によって、係数の2乗和にペナルティを課すため、すべての特徴量の係数を小さくする傾向があります。例え、不要な特徴量があっても係数を完全にはゼロにしないということですね。そのため、特徴選択よりもモデルの汎化性能を向上させたい場合に適しています。ただし、Lasso回帰の方が過学習を防ぐ性能は高いと言えます。

正則化項のハイパーパラメータである $\lambda$ はペナルティの大きさを制御しており、 $\lambda$ が大きいほどペナルティが大きくなる（係数が小さくなる）ということになります。

通常はこの $\lambda$ はの値は小さいと正則化効果が弱くなり、過学習のリスクが増します。逆に大きすぎるとモデルが単純すぎて予測精度が下がることもあります。そのため、一般的にはクロスバリデーションを使って最適な値を探索します。

また、LassoとRidge回帰の使い分けは場合によりますが、まずはRidge回帰で重要そうなパラメータを確認した後に、よりモデルの解釈性を上げたい（特徴量を絞りたい）場合はLassoを使用するのがいいと考えています。

Lasso & Ridge回帰をPythonで比較

それでは実際に通常の重回帰分析とLasso、Ridge回帰でどの程度回帰性能が異なるのかをPythonで実行することで比較してみましょう。

今回のコードだと、 $\hat{y} = w_0 + w_1 X + w_2 X^2 + \ldots + w_d X^{25}$ の式で示される25個の回帰係数を決めてy=sin(x)にフィットするように学習してくださいというお題になります。

わかりやすいように予測した特徴量の係数とテストデータに対するMSE（平均二乗誤差）を出力しました。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.metrics import mean_squared_error

# データ生成
np.random.seed(0)
X_train = np.linspace(-3, 3, 50)  # 10個のトレーニングデータ点を生成
y_train = np.sin(X_train) + np.random.normal(0, 0.2, size=X_train.shape)  # 正弦関数にノイズを追加

X_test = np.linspace(-3, 3, 100)  # より多くのテストデータ点を生成
y_test = np.sin(X_test)  # ノイズのない正弦関数を生成

# 多項式特徴量の追加
poly_degree = 25  # 高次の多項式を使用して過学習を起こす
poly_features = PolynomialFeatures(degree=poly_degree, include_bias=False)

X_train_poly = poly_features.fit_transform(X_train[:, np.newaxis])
X_test_poly = poly_features.transform(X_test[:, np.newaxis])

# モデルの学習
model_normal = LinearRegression()
model_normal.fit(X_train_poly, y_train)

model_lasso = Lasso(alpha=0.01)  # alphaは正則化パラメータ
model_lasso.fit(X_train_poly, y_train)

model_ridge = Ridge(alpha=0.1)  # alphaは正則化パラメータ
model_ridge.fit(X_train_poly, y_train)

# トレーニングデータとテストデータでの予測
y_train_pred_normal = model_normal.predict(X_train_poly)
y_test_pred_normal = model_normal.predict(X_test_poly)

y_train_pred_lasso = model_lasso.predict(X_train_poly)
y_test_pred_lasso = model_lasso.predict(X_test_poly)

y_train_pred_ridge = model_ridge.predict(X_train_poly)
y_test_pred_ridge = model_ridge.predict(X_test_poly)

# MSEの計算
mse_normal = mean_squared_error(y_test, y_test_pred_normal)
mse_lasso = mean_squared_error(y_test, y_test_pred_lasso)
mse_ridge = mean_squared_error(y_test, y_test_pred_ridge)

# 回帰係数の取得
df_normal_coefs = pd.DataFrame({"Normal Coefficients": model_normal.coef_})
df_lasso_coefs = pd.DataFrame({"Lasso Coefficients": model_lasso.coef_})
df_ridge_coefs = pd.DataFrame({"Ridge Coefficients": model_ridge.coef_})

# 係数データフレームの結合
df_coef = pd.concat([df_normal_coefs, df_lasso_coefs, df_ridge_coefs], axis=1)

# 結果のプロット
plt.figure(figsize=(12, 8))

# 正解のプロット
plt.plot(X_test, y_test, label='True function', color='green')

# 予測のプロット
plt.plot(X_test, y_test_pred_normal, label='Normal model prediction', color='blue', linestyle='--')
plt.plot(X_test, y_test_pred_lasso, label='Lasso model prediction', color='red', linestyle='--')
plt.plot(X_test, y_test_pred_ridge, label='Ridge model prediction', color='orange', linestyle='--')

# トレーニングデータのプロット
plt.scatter(X_train, y_train, label='Training data', color='black')

plt.xlabel('X')
plt.ylabel('y')
plt.title('Overfitting Example with Polynomial Regression')
plt.legend()
#plt.show()
plt.savefig('graph.png')

# 回帰係数の出力
print("Regression Coefficients:\n", df_coef)

# MSEの出力
print("\nNormal Model MSE:", mse_normal)
print("Lasso Model MSE:", mse_lasso)
print("Ridge Model MSE:", mse_ridge)

'''
Regression Coefficients:
     Normal Coefficients  Lasso Coefficients  Ridge Coefficients
0             -0.197344        8.549774e-01        1.136630e+00
1              0.574083        0.000000e+00       -1.156902e-01
2             15.426225       -8.480762e-02       -2.529196e-01
3             -3.238403       -1.037514e-02       -1.159110e-01
4            -51.063047       -6.826189e-03       -2.615471e-01
5              6.035358        1.367322e-03        2.825175e-02
6             76.264491        2.464039e-04        7.167233e-02
7             -6.164472        2.370437e-04        1.354192e-01
8            -64.458579        2.572652e-05        1.198943e-01
9              4.071624       -2.993244e-06        4.272102e-02
10            34.206110        1.438850e-06        1.541273e-02
11            -1.810542       -1.849534e-06       -1.447259e-01
12           -12.032257        1.239650e-07       -9.247012e-02
13             0.542904       -2.224174e-07        8.427362e-02
14             2.878871        1.141321e-08        5.305983e-02
15            -0.108857       -1.773508e-08       -2.407649e-02
16            -0.470794        7.889044e-10       -1.463769e-02
17             0.014311       -8.049821e-10        3.924339e-03
18             0.051784        1.335531e-11        2.295029e-03
19            -0.001181        4.546795e-11       -3.723504e-04
20            -0.003662       -7.319172e-12       -2.092187e-04
21             0.000055        1.859530e-11        1.919651e-05
22             0.000150       -1.677709e-12        1.035714e-05
23            -0.000001        3.321028e-12       -4.165391e-07
24            -0.000003       -2.588140e-13       -2.157051e-07

Normal Model MSE: 0.03492194119927194
Lasso Model MSE: 0.009979363887785631
Ridge Model MSE: 0.025455118945035337

'''

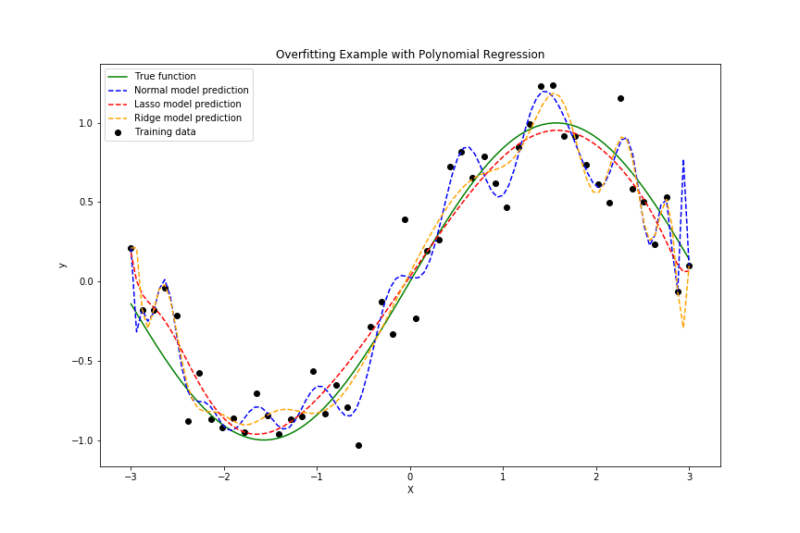
出力されたグラフは以下の通りとなっております。

緑線：真の関数
青線：通常の重回帰
黄線：Ridge回帰
赤線：Lasso回帰

重回帰は過学習気味であることがわかります。一方、Ridge回帰やLasso回帰はきちんと曲線を描いており、Lasso回帰が最も真の関数に近そうですね。

また、MSEからも通常の重回帰は、学習データにはよく当てはまるものの、テストデータに対してはやや過学習気味で誤差が大きめです。Ridge回帰では係数が抑えられることで、過学習が少し軽減され、MSEも改善しています。Lasso回帰は不要な特徴量を自動的に無視（係数をゼロに）するため、最も高い予測精度を示しています。

モデル	平均二乗誤差（MSE）
通常の重回帰	0.0349
Ridge回帰	0.0255
Lasso回帰	0.0100

終わりに

いかがでしたか？Lasso回帰とRidge回帰は、どちらも「過学習対策」として非常に有効です。モデルの予測性能を保ちつつ、シンプルで解釈しやすいモデルを作れるのは大きなメリットですね。特にLassoは特徴量が多い場面や、どの変数が重要か知りたい場面で役立ちます。今後の分析やモデリングにぜひ活かしてみてください！