ロジスティック回帰についてわかりやすく説明

こんにちは！ぼりたそです！

今回は 「ロジスティック回帰」 について、初学者の方にもわかりやすいように解説していきます。

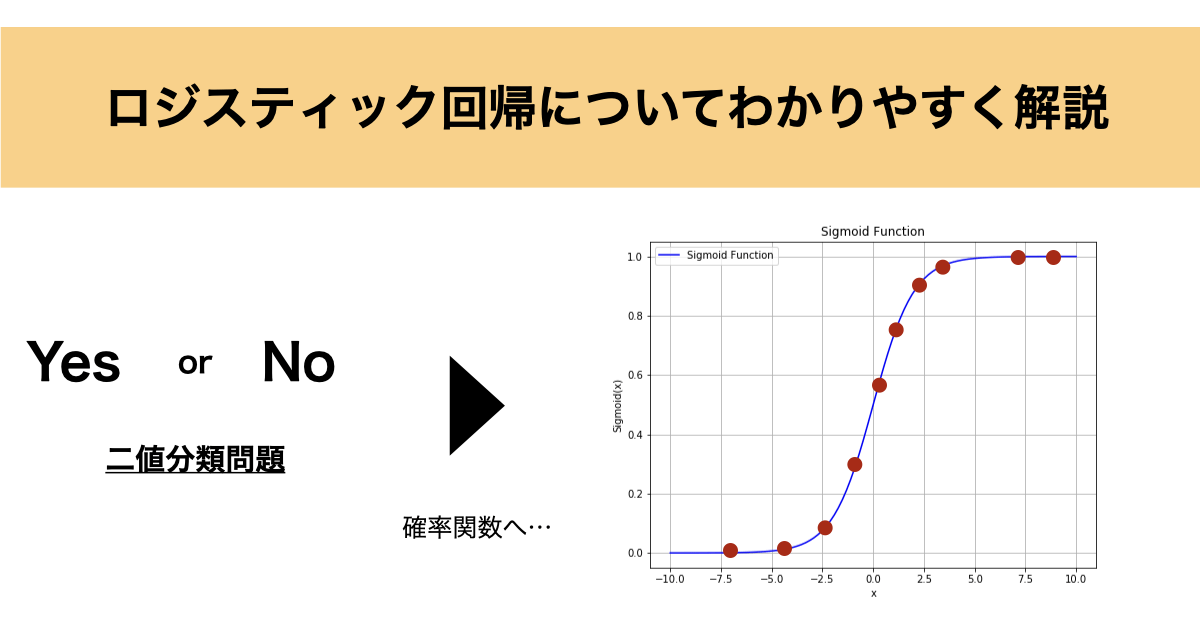
ロジスティック回帰は、Yes / No のような 二値分類問題 に対して使われる代表的な手法です。例えば「スパムメールか否か」「顧客が購入するか否か」など、日常的にもよくある問題ですね。

ただし、数学的な背景には少し難しい部分もあるため、本記事ではできるだけ噛み砕いて説明していきます！

この記事は以下のポイントでまとめています。

Point

ロジスティック回帰とは？
　
回帰係数の決定
　
編回帰係数の解釈
　
ロジスティック回帰の注意点

また、CSVファイルを学習データとして入力するだけでロジスティック回帰を実行するPythonコードも紹介しているので、ご興味ある方は以下の記事を参照ください。

合わせて読みたい

それでは詳細に説明していきます。

ロジスティック回帰とは？
偏回帰係数の解釈について
ロジスティック回帰の注意点
終わりに

ロジスティック回帰とは？

ロジスティック回帰は、Yes/No、成功/失敗、1/0 など、2つのカテゴリ に分類したいときに使われる回帰モデルです。

たとえば：

メールがスパムかどうか
顧客が商品を購入するかどうか
患者が病気であるかどうか

このような「分類問題」に対し、確率として予測 を行うことができる点がロジスティック回帰の魅力です。

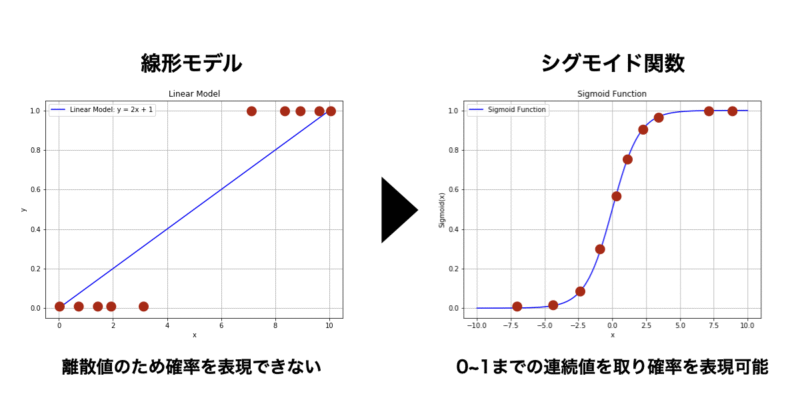
線形モデルとシグモイド関数

ロジスティック回帰も、まずは線形結合を用いて以下のような式を立てます。
$\beta$ は回帰係数になります。

$$z = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n$$

しかし、このままでは $z$ は $-\infty$ から $\infty$ までの値を取るため、「確率」としては使えません。

そこで、以下のような シグモイド関数（ロジスティック関数）を使って出力を 0〜1 の範囲に変換します。

$$p(x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n)}}$$

この出力 $p(x)$ が、「1になる確率」 を意味します。

偏回帰係数の推定

それでは次に偏回帰係数の推定について説明していきます。

通常の回帰モデルでは最小二乗法を使用して偏回帰係数を推定しますが、ロジスティック回帰は確率関数で表されるので最尤推定を使用して回帰係数を推定していきます。

最尤推定については以下の記事にまとめてありますので、ご参考にしていただければ思います。

合わせて読みたい

最尤推定を実行するにはまず、尤度関数を設定する必要があります。

まず、ロジスティック回帰における尤度関数の形は、データがベルヌーイ分布に従うという前提に基づいています。
ベルヌーイ分布とは一回の試行で二つの事象の内どちらかが確率 $p$ で起こる時に以下の関数で表すことができます。

$$P(y_i) = p_i^{y_i} (1 – p_i)^{1 – y_i} \\$$

$y_i$ は試行の結果（0または1）
$p_i$ は $y_i$ の成功確率（ロジスティック関数：$p(y) = \frac{1}{1 + e^{-y_i}}$）
$y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \ldots + \beta_n x_{in} \\$

ロジスティック回帰では全ての観測データが独立だと仮定すると、全データに対する尤度関数は以下のとおり各データの確率の掛け算となります。なお、 $y_i$ は $\beta$ に依存するため $\beta$ の関数として表しています。

$$L(\beta) = \prod_{i=1}^{N} p_i^{y_i} (1 – p_i)^{1 – y_i} \\$$

この尤度関数のままでは計算がしづらいので対数をとりー（マイナス）をかけて、以下のような対数尤度関数として扱うこととします。マイナスをかけているのは対数尤度関数が最小になるようなパラメータ $\beta$ を求めるためです。

$$log L(\beta) = −\sum_{i=1}^{N} \left[ y_i \log(p_i) + (1 – y_i) \log(1 – p_i) \right] \\$$

この対数尤度関数が最小になるような $\beta$ を求めていきます。最小となる点は偏微分関数＝０となる場合です。実際に全ての $\beta$ について偏微分を行うと以下のような簡単な関数になります。

$$\frac{\partial J(\beta)}{\partial \beta_j} = \frac{1}{N} \sum_{i=1}^{N} (p_i – y_i) x_{ij} \\$$

勾配降下法での最適化

しかし、この偏微分した関数は非線形のため、解析的に0となる $\beta$ を計算することが困難です。

そのため、勾配降下法という手法を用います。

勾配降下法は、関数の最小値を見つけるための反復的な手法です。具体的には、関数の勾配（傾き）を利用して、関数の値が減少する方向にパラメータを更新していきます。

わかりやすい例えで言うと、山の頂上から谷底へと降りていくプロセスを想像してください。山の傾きを調べて、最も急な降り方向に進む、これを何度も繰り返すことで、最終的に谷底（関数の最小値）に到達することを目指します。

具体的な最適化手法としては以下の通りです。

パラメータ（ $\beta$ ）の初期値をランダムに設定します。
　
目的関数のパラメータに対する勾配を計算します。勾配は、関数の各パラメータ $\beta$ に対する偏微分 $\frac{\partial J(\beta)}{\partial \beta_j}\\$ で表されます。
　
勾配の逆方向にパラメータを更新します。更新式は次のようになります：
$$\beta_j := \beta_j – \alpha \frac{1}{N} \sum_{i=1}^{N} (p_i – y_i) x_{ij}\\$$
・$\alpha$ は学習率
・$\frac{\partial J(\beta)}{\partial \beta_j}$ は対数尤度関数の偏微分した式であり、勾配にあたる
　
目的関数の変化が非常に小さくなるか、あらかじめ設定した最大反復回数に達するまで、2と3のステップを繰り返します。

学習率 $\alpha$ は勾配に対してどれだけ進むかを表しており、大きすぎると最小値を過ぎてしまい解が収束せず、小さすぎると最小化まで膨大な時間がかかってしまいます。

長くなりましたが、この勾配降下法を使用して最小となる偏回帰係数 $\beta$ が最も尤もらしい値として推定できます。

偏回帰係数の解釈について

では次に偏回帰係数の解釈について説明していきます。

偏回帰係数は目的変数が1となる確率にどれだけ影響するかを表しています。

その影響度はオッズ比として定義されており、

$$\text{オッズ比} = e^{\beta_j} \\$$

と表すことができ、自然対数関数の $\beta$ 乗となります。

例えば、偏回帰係数が1の時、オッズ比は以下のようになります。

$$\text{オッズ比} = e^{1} = 2.718\\$$

この場合、説明変数Xが1単位増加した時に目的変数Yが1となる確率が2.7倍になることを意味しています。

このように偏回帰係数からオッズ比を算出し、目的変数Yの確率にどれだけ影響を与えるかを見積もることができます。

ロジスティック回帰の注意点

ここまでロジスティック回帰の基本的な原理について説明してきましたが、最後にロジスティック回帰を扱う上で注意しなければいけない点について説明して聞きます。

注意点は以下に示す通りです。

データのスケーリング:
ロジスティック回帰では、入力データのスケーリングが重要です。特に勾配降下法を用いる場合、データの範囲を統一することで収束が速くなり、モデルの性能が向上します。スケーリングの主な手法としては標準化（平均を0、標準偏差を1にする）や正規化（最小を0、最大を1にする）を行います。