どの回帰モデルを選べばいい？代表的手法6つを比較

機械学習で「数値を予測したい」と思ったとき、“どの回帰手法を使えばいいのか？”という悩みではないでしょうか？

線形回帰はシンプルだけど非線形な関係には弱い。ランダムフォレストは精度が高いけど中身が見えにくい。GPRは不確実性まで出せるけど計算が重たい…。モデルによって特徴も向き不向きもさまざまです。

この記事では、代表的な6つの回帰手法（重回帰、Lasso、Ridge、ランダムフォレスト、SVR、GPR）について、それぞれの特徴・数式・メリット/デメリットを整理しながら、最後にPythonを使って実際のデータで性能比較してみます。

「どのモデルを選べばいいか迷っている」「違いを体系的に理解したい」という方は、ぜひ参考にしてみてください。

それでは順に解説していきます。

回帰手法比較

まずは、代表的な回帰モデルを一覧表で整理し、それぞれの特徴や利点・欠点を比較してみましょう。

この表を通じて、モデル同士の違いや向いているケースを俯瞰的に捉えることができます。特に、解釈性・精度・柔軟性・計算コストといった観点で選ぶ際に、参考になる比較になっています。

どの回帰モデルを使うべきか迷ったときは、以下のフローチャートを参考にしてみてください。
データの性質（線形性・特徴量の多さ・データ数）や目的（解釈性重視か・予測精度重視か）に応じて、適切な手法が見えてきます。

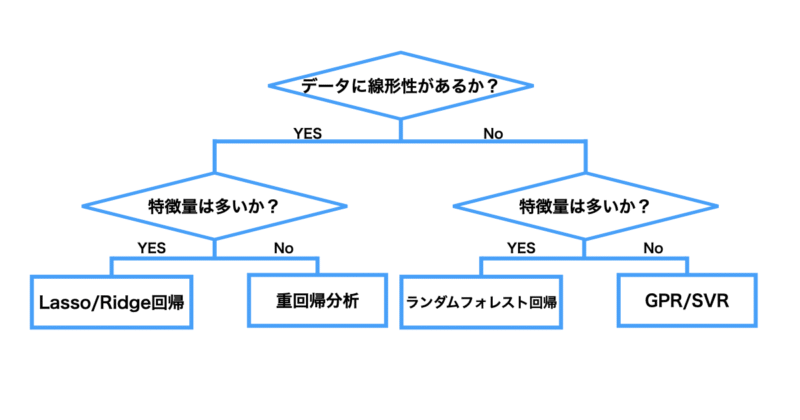
以下はフローチャートの補足説明となっております。

• 線形関係があるか？
  → 相関係数が高い、あるいは散布図から直線関係が見られるような場合は線形関係がある可能性が高いです。
  　
• 特徴量が多いか？
  → 個人的な所感ですがおおよそ30次元以上が目安です。それ未満なら「少ない」と考えています。また、特徴量の次元数が多くてもデータ数が十分にあれば精度の良い学習モデルが構築できます。逆に次元数が少ないがデータ数も少ない場合は注意が必要です。
  　
• データ数が少ないか？
  → 一般的には300件以下を「少ない」と見なします。これを超えると GPR などでは計算が重くなりがちです。
  　
• Lasso vs Ridge
  → Lasso は不要な変数をゼロにして削るため、変数選択を兼ねたい場合に便利
  → Ridge はすべての変数を残す代わりにバランスをとるため、安定性や多重共線性が気になるときに適しています。
  　
• SVR vs GPR
  → 学習モデルに不確実性も求めるのであればGPRが適していると言えます。
  　

このように、単に精度が高いから・よく使われているから、という理由だけで選ぶのではなく、データの性質と目的に応じて使い分けることが重要です。フローチャートと比較表を併用することで、より実務的な判断の一助となれば幸いです。

各手法の概要とアルゴリズム

ここでは、前章で一覧比較した各回帰モデルについて、もう少し詳しく掘り下げていきます。
それぞれのモデルがどのようなアルゴリズムで予測を行っているのか、数式や仕組みの観点から簡潔に解説します。

とはいえ、本記事では初学者の方にも理解しやすいように、数学的な細部には踏み込まず、直感的な理解が得られるレベルにとどめています。

モデルの動作原理をざっくりとつかむことで、実際のデータにどのように適用できるかのイメージを持ちやすくなるはずです。

重回帰分析

重回帰分析は、統計学や機械学習の中でもよく用いられる分析手法の一つです。主に、複数の説明変数（特徴量）と1つの目的変数（ターゲット）との関係を分析するのに使われます。

例えば、ある店舗の売上を広告費と入店者数から予測するとします。

■説明変数

• 広告費（円）：どれくらい店舗の広告に費用をかけたか
• 入店者数（人）：どれくらいの人が店舗に入店したか

■目的変数

• 店舗の売上（円）：どれくらい店舗で売上があったか

重回帰分析では、これらのデータを使って、目的変数である「売上」を説明変数である「広告費」「入店者数」から予測することが目的です。

数学的に表現すると、重回帰分析では以下のようなモデルを考えます

売上 = $a_0$ + $a_1$ × 広告費 + $a_2$ × 入店者数

ここで、$a_0$ は切片を表し、$a_1$, $a_2$はそれぞれ回帰係数と呼ばれるもので、変数の相関関係や重要度を把握することができます。

この回帰係数については最小二乗法を用いて決定します。

最小二乗法とは関数が$y = a_1x_1 + a_2x_2 + \ldots + a_jx_n$ ($a_j$は変数の係数)であるときに以下の損失関数が最小となるように変数の係数を決定する手法です。

■最小二乗法

$$\sum_{i=1}^{N} \left( y_i – \sum_{j=1}^{n} a_j x_{ij} \right)^2$$

重回帰分析は計算コストも低く、回帰モデルの解釈性も高いですがデータが線形関係にあることが前提となっていることに注意が必要です。

重回帰分析については以下の記事で詳細に解説しているので、ぜひご参考になさって下さい。

合わせて読みたい

【初心者向け】重回帰分析についてわかりやすく説明

重回帰分析について初学者向けにまとめました。「重回帰分析とは何か？」、「メリット、デメリットは？」などわかりやすくまとめていますのでご覧ください

boritaso-blog.com

2023.07.30

Lasso回帰

先ほど紹介した重回帰分析では最小二乗法を用いて変数の係数を決定していました。

しかし、最小二乗法では過学習に陥ることがあり、その場合、係数 $a_j$ が極端に大きくなる場合があります。

Lasso回帰はこの過学習を防ぐために以下式のようにL1正則化項を導入して係数を決定する回帰手法です。

$$\sum_{i=1}^{N} \left( y_i – \sum_{j=1}^{n} a_j x_{ij} \right)^2 + \lambda \sum_{j=1}^{n} |a_j|$$

L1正則化項によって係数の絶対値の和にペナルティを課すため、不要な特徴量の係数をゼロにする傾向があります。

ハイパーパラメータである $\lambda$ はペナルティの大きさを制御しており、 $\lambda$ が大きいほどペナルティが大きくなる（係数が小さくなる）ということになります。

そのため、Lasso回帰は特徴量の選択が重要な場合や、モデルの解釈性を高めたい場合に適しています。一方で重回帰分析と同様に目的変数と特徴量が線形関係にあることが前提となっているので注意が必要です。

Lasso回帰については以下の記事で詳細に解説していますので、ご参考になさって下さい。

合わせて読みたい

Lasso & Ridge回帰についてわかりやすく説明

この記事はLasso & Ridge回帰についてわかりやすく説明したものになります。具体的には、「過学習とは」、「正則化とLasso & Ridge回帰」、「LassoとRidge回帰の違い」、「Pythonでの性能比較」について解説しています。

boritaso-blog.com

2024.04.07

Ridge回帰

Ridge回帰も最小二乗法による過学習を防ぐためにL2正則化項を用いて係数を決定する回帰手法になります。

$$\sum_{i=1}^{N} \left( y_i – \sum_{j=1}^{n} a_j x_{ij} \right)^2 + \lambda \sum_{j=1}^{n} a_j^2$$

L2正則化項によって、係数の2乗和にペナルティを課すため、すべての特徴量の係数を小さくする傾向があります。

また、ハイパーパラメータである $\lambda$ はペナルティの大きさを制御しており、 $\lambda$ が大きいほどペナルティが大きくなる（係数が小さくなる）ということになります。

L2正則化はL1正則化と異なり、不要な特徴量があっても係数を完全にはゼロにはしません。そのため、特徴量同士が多重共線性がある場合に適しています。

一方で重回帰分析と同様に目的変数と特徴量が線形関係にあることが前提となっているので注意が必要です。

Ridge回帰については以下の記事で詳細に解説していますので、ご参考になさって下さい。

合わせて読みたい

Lasso & Ridge回帰についてわかりやすく説明

この記事はLasso & Ridge回帰についてわかりやすく説明したものになります。具体的には、「過学習とは」、「正則化とLasso & Ridge回帰」、「LassoとRidge回帰の違い」、「Pythonでの性能比較」について解説しています。

boritaso-blog.com

2024.04.07

ランダムフォレスト回帰

ランダムフォレスト（Random Forest） とは、複数の決定木を組み合わせて予測を行うアンサンブル学習の一手法です。

具体的には、以下のようなアルゴリズムになっています：

1. 学習データをランダムに何度も抽出して（※ブートストラップ法）、複数のデータセットを作ります。
   　
2. それぞれのデータセットに対して、特徴量をランダムに選びながら決定木を構築します。
   　
3. 各決定木の予測を集約して最終的な予測を行う
   • 分類の場合：多数決でクラスを決定
   • 回帰の場合：予測値の平均を算出

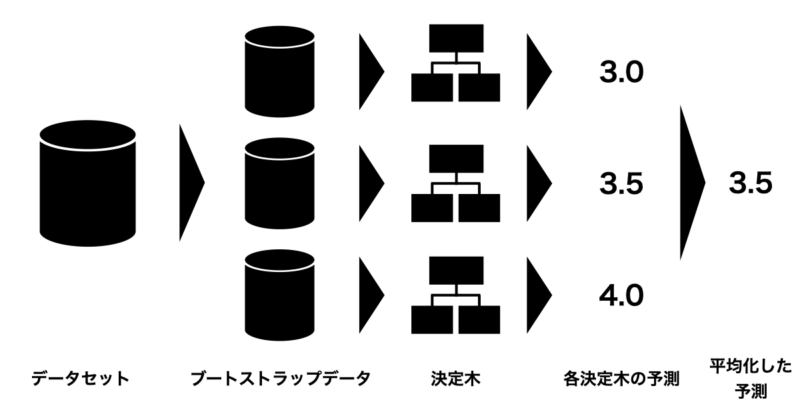
ランダムフォレストは特徴量が多い場合でもサブサンプリング特性により学習精度が高い傾向にあるのが特徴です。一方で大規模な学習データは計算コストが高く注意が必要になります。

ランダムフォレスト回帰については以下の記事で詳細に解説していますので、ご参考になさって下さい。

合わせて読みたい

【コード付】ランダムフォレストについてわかりやすく解説

この記事はランダムフォレストについて解説した記事になります。具体的にはランダムフォレストとは？、使用するメリット、デメリット、実行する手順、Pythonでの実装について詳細に解説しています

boritaso-blog.com

2024.02.05

サポートベクター回帰（SVR）

サポートベクター回帰（SVR）は、サポートベクターマシン（SVM）を応用した回帰手法であり、一般の回帰手法と同様にデータに対して最適な回帰モデルを構築し、新しいデータの値を予測することが目的です。

ただし、他の回帰モデルと異なるのは、「すべてのデータ点を正確に通る必要はない」という考え方です。

代わりに、一定の誤差範囲（εチューブ）内になるべくデータ点が収まるような回帰線を見つけます。これにより過学習を防ぎ、汎化性を向上することができます。

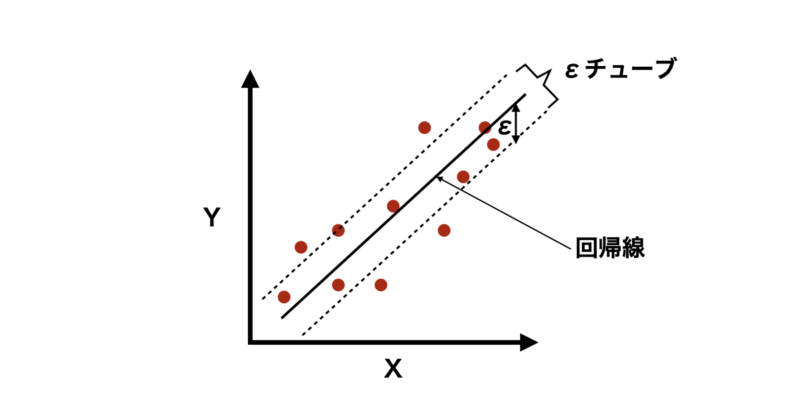
では、数式的な説明も含めて具体的なアルゴリズムについて紹介していきます。

サポートベクター回帰のアルゴリズムとしては一定の誤差範囲（εチューブ）内にデータ点が収まるような回帰線を見つけることですが、具体的には以下の最小化問題を解くことにあたります。

$$\min_{w, b, \xi^{+}, \xi^{-}} \frac{1}{2} \require{physics}\norm{w}^2 + C \sum_{i=1}^n (\xi_i^{+} + \xi_i^{-})$$

ここで：

• $w$：各変数の重みベクトル
• $b$：バイアス項
• $\xi_i^{+}, \xi_i^{-}$​：スラック変数（許容誤差を超える部分を表す）
• $C$：正則化パラメータ（変数の重みと許容誤差のトレードオフを制御）

数式の内容を説明すると、

まず、第一項：$\frac{1}{2} \require{physics}\norm{w}^2$ は正則化項になります。

具体的には、重みベクトル $w$ のノルム（長さ）の二乗を最小化することで、モデルが極端に複雑になるのを防ぎます。

この項により重み $w$ が極端に大きくなったり小さくなったりして、モデルが学習データに対して過学習を起こすリスクを軽減してくれます。

次に第二項：$C \sum_{i=1}^n (\xi_i^{+} + \xi_i^{-})$ はデータ点の誤差（$\epsilon$-チューブを超えた部分）を表す項です。

$\xi_i^{+}$, $ \xi_i^{-}$はそれぞれ$\epsilon$-チューブの上側、下側からどれだけ外れているかを表している誤差の変数になります。

$\epsilon$-チューブ外の誤差を抑えることで、モデルがデータに対して適切にフィットするようにします。

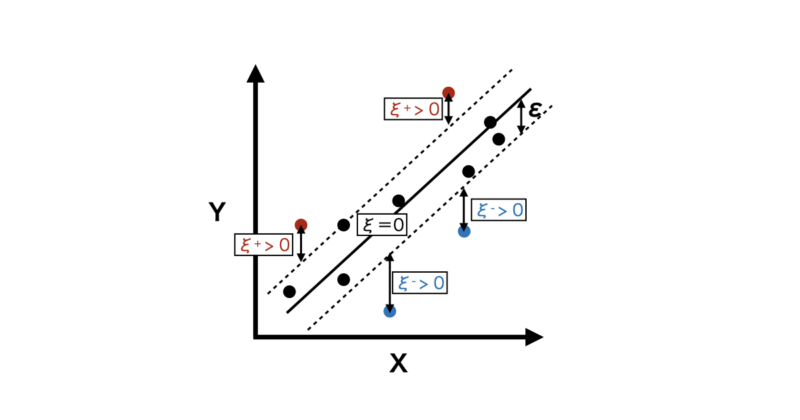
また、$C$ はハイパーパラメータであり、第一項（モデルの複雑さ）と第二項（誤差）とのバランスを調整します。

• $C$ が大きい場合：誤差を小さくすることを優先（高精度だが過学習のリスクが高い）。
• $C$ が小さい場合：モデルの複雑さを抑えることを優先（汎化性能が高いが精度が低下する可能性）。

以上の条件を満たしながら最適化関数を最小化することで以下のような回帰式を求めることができます。

$$\hat{y} = w^\top x + b$$

SVRは非線形なデータにも対応できる柔軟性を持ち、少数データやノイズの多いデータにも比較的強いという利点があります。

一方で学習データの数に対して特徴量の数が多すぎると学習精度が著しく低くなるので注意が必要です。

SVRについては以下の記事で詳細に解説していますので、ご参考になさって下さい。

合わせて読みたい

サポートベクター回帰（SVR）についてわかりやすく解説

サポートベクター回帰（SVR）についてわかりやすく解説した記事になります。具体的には「サポートベクター回帰（SVR）とは？」、「サポートベクター回帰（SVR）のアルゴリズム」、「Pythonにて実行」、「非線形問題への拡張」

boritaso-blog.com

2024.12.30

ガウス過程回帰（GPR）

みなさんは、こんな課題に直面したことはないでしょうか？

予測だけでなく「その予測がどれくらい信用できるか」という情報も知りたい

こうした課題に非常に有効なのが、ガウス過程回帰（Gaussian Process Regression, GPR） です。

ガウス過程回帰（GPR）は、予測値だけでなく「その予測がどれくらい信頼できるか（不確実性）」も同時に出力できる回帰手法です。特に、データが少ない場合や、予測の信頼度が重要なタスクで効果を発揮します。

GPRは「関数の分布」をガウス過程という確率モデルで捉えます。入力と出力の関係を

$$f(x) \sim GP(m(x), k(x, x’))$$

とし、任意の入力 $x$ に対して予測分布（平均と分散）を求めます。ここで $m(x)$ は平均関数、$k(x, x’)$ はカーネル関数で、入力間の類似度を表します。

予測点 $x_*$​ における出力は、以下のように平均 $\mu_*$​ と分散 $\sigma_*^2$​ で表されます：

$$\mu_* = k_*^T (K + \sigma_n^2 I)^{-1} y$$

$$\sigma_*^2 = k(x_*, x_*) – k_*^T (K + \sigma_n^2 I)^{-1} k_*$$

ここで $K$ は訓練データ間の共分散行列、$k_*$​ は訓練データと新規点とのカーネルベクトル、$\sigma_n^2$​ はノイズ分散です。

GPRの利点は、不確実性を含めた予測が可能なことと、カーネルを通じて非線形な関係も柔軟に表現できる点にあります。反面、計算コストが高く、データが多すぎると非効率になるため、適用範囲には注意が必要です。

とはいえ、これだけだとあまりイメージが湧かないと思いますので、実際にガウス過程回帰をしたグラフを下に示します。

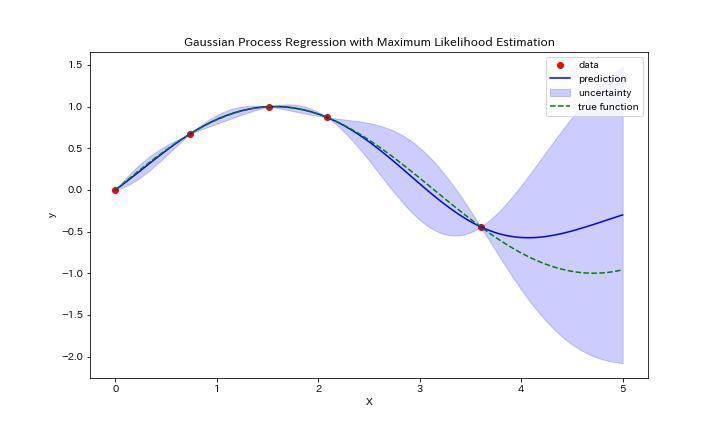
このグラフはy＝sin(x)に従う5点（赤点）を入力データとしてガウス過程回帰を実行した結果になります。緑の破線が真のグラフであるのに対して、青線が予測のグラフになっています。

さらに、青色で塗りつぶされているのが予測の分散になります。真のグラフに対してデータが少ない領域は分散が大きく、予測値も外れていることがわかりますね。

このように入力データに対して、予測値とその分散を出力できるのがガウス過程回帰になります

最近ではベイズ最適化においてガウス過程回帰の使用が増えており、実務や研究でも注目度が高まっています。

GPRについては以下の記事で詳細に解説していますので、ご参考になさって下さい。

合わせて読みたい

【初心者向け】ガウス過程回帰をわかりやすく説明〜Pythonで実装してみた〜

ベイズ最適化でも使用されるガウス過程回帰について初学者の方にもイメージを掴んでいただけるように解説した記事です。Pythonでガウス過程回帰を実行するコードも紹介しています。

boritaso-blog.com

2023.07.23

Pythonにて実装&比較

ここでは、代表的な回帰モデル6種（重回帰分析・Lasso・Ridge・ランダムフォレスト・SVR・GPR）を用いて、実際のデータでどのモデルがどのような特徴を持つかを比較検証します。

以下の3パターンの仮想データを用意し、各モデルの性能を10-Foldクロスバリデーションで評価しました：

各ケースで 10Fold CV(10分割交差検証)を実行し、R²（決定係数）、MSE（平均二乗誤差）、MAE（平均絶対誤差）からモデルの汎化性能を評価しました。

実行に使用したPythonコードは以下の通りです。

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import Matern
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error, make_scorer
from sklearn.model_selection import KFold, cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline

# 設定
RANDOM_STATE = 0
N_SAMPLES = 300

def generate_data_all_features_used(case):
    np.random.seed(RANDOM_STATE)
    
    if case == 1:
        X = np.random.randn(N_SAMPLES, 15)
        coef = np.random.uniform(-2, 2, size=15)
        y = X @ coef + np.random.randn(N_SAMPLES) * 0.5
    elif case == 2:
        X = np.random.randn(N_SAMPLES, 15)
        y = (
            np.sin(X[:, 0]) + X[:, 1]**2 + np.log(np.abs(X[:, 2]) + 1)
            + np.exp(-X[:, 3]) + X[:, 4]*X[:, 5] + X[:, 6]**3
            + np.tanh(X[:, 7]) + np.abs(X[:, 8])
            + X[:, 9]*X[:,10] + X[:,11] + X[:,12]**2
            - X[:,13] + X[:,14]
            + np.random.randn(N_SAMPLES) * 0.5
        )
    elif case == 3:
        X = np.random.randn(N_SAMPLES, 30)
        y = (
            np.sum(np.sin(X[:, 0:5]), axis=1) +
            np.sum(np.cos(X[:, 5:10]), axis=1) +
            np.sum(np.log(np.abs(X[:, 10:12]) + 1), axis=1) +
            np.sum(np.sqrt(np.abs(X[:, 12:14]) + 1), axis=1) +
            np.sum(np.exp(-np.abs(X[:, 14:16])), axis=1) +
            np.sum(np.tanh(X[:, 16:18]), axis=1) +
            X[:, 18] * X[:, 19] +
            np.sum(X[:, 20:25] ** 2, axis=1) +
            X[:, 25] * X[:, 26] + X[:, 27] ** 3 - X[:, 28] + np.abs(X[:, 29]) +
            np.random.randn(N_SAMPLES) * 0.5
        )
    return X, y

# 評価指標
scorers = {
    "R2": make_scorer(r2_score),
    "MSE": make_scorer(mean_squared_error, greater_is_better=False),
    "MAE": make_scorer(mean_absolute_error, greater_is_better=False),
}

cv_results = []

# 各ケースを評価
for case in [1, 2, 3]:
    X, y = generate_data_all_features_used(case)
    n_features = X.shape[1]  # 特徴量数を動的に取得
    kf = KFold(n_splits=10, shuffle=True, random_state=RANDOM_STATE)
    
    # モデル定義（都度GPRの次元数を更新）
    models = {
        "LinearRegression": LinearRegression(),
        "Lasso": Lasso(alpha=0.1),
        "Ridge": Ridge(alpha=1.0),
        "RandomForest": RandomForestRegressor(random_state=RANDOM_STATE),
        "SVR": make_pipeline(StandardScaler(), SVR(C=2.0, epsilon=0.1)),
        "GPR": make_pipeline(
            StandardScaler(),
            GaussianProcessRegressor(
                kernel=Matern(length_scale=np.ones(n_features)),
                random_state=RANDOM_STATE,
                n_restarts_optimizer=0
            )
        )
    }
    
    for name, model in models.items():
        row = {"Case": f"Case {case}", "Model": name}
        for metric, scorer in scorers.items():
            scores = cross_val_score(model, X, y, cv=kf, scoring=scorer)
            row[metric] = np.mean(scores) * (-1 if metric in ["MSE", "MAE"] else 1)
        cv_results.append(row)

# 結果表示
results_df = pd.DataFrame(cv_results)
print(results_df)

それでは各Caseごとに結果を見ていきます。

Case1（線形問題、特徴量15個）

Case1の結果は以下のテーブルの通りです。

線形問題ということもあり、重回帰分析、Lasso回帰、Ridge回帰のモデル性能が高いようです。

一方でSVRやGPRも予測性能は高く、解釈性や計算コストを重視するのであれば重回帰分析やLasso回帰を用いるのが最適と言えます。

Case2（非線形問題、特徴量15個）

Case2の結果は以下のテーブルに示す通りです。

非線形問題ということもあり、線形回帰である重回帰、Lasso、Ridgeは性能が低いことがわかります。

一方で非線形問題にも対応できるランダムフォレストやGPRは良い性能を示しています。データ数が〜300個であり、特徴量が20個程度であればGPRが最適と言えます。

Case3（非線形問題、特徴量30個）

Case3の結果は以下のテーブルに示しています。

非線形問題でかつ特徴量も30個と多いためGPRやSVRもあまりモデル性能が悪い結果となりました。

一方でランダムフォレスト回帰については他のモデルと比較してモデル性能が良い結果となりました。

ランダムフォレストでは、各決定木を構築する際にランダムに特徴量を選ぶ（特徴量サブサンプリング）という仕組みがあります。

そのため、特徴量が30個以上のような高次元のデータでも比較的安定した性能を発揮できました。

まとめ

本記事では、代表的な回帰モデル6種（重回帰分析、Lasso回帰、Ridge回帰、ランダムフォレスト回帰、SVR、ガウス過程回帰）について、それぞれの特徴・メリット・デメリットを整理し、さらに実際のデータ生成＆Pythonによる性能比較を通じて、どのような状況でどのモデルが適しているかを詳しく検証しました。

回帰モデルを選ぶ際には、「線形 or 非線形」「データ数・特徴量の多さ」「解釈性 or 精度」「予測の信頼度の必要性」といった観点から整理し、目的に応じた最適なモデルを選ぶ視点を持っておくことが重要です。

この記事が、回帰モデル選びに迷ったときの“地図”として役立つことを願っています！