こんにちは!ぼりたそです!
重回帰分析は、統計学や機械学習において広く使われている回帰手法の一つです。
この記事では、重回帰分析の基本から、メリット・デメリット、変数の重要度、多重共線性とその対処法までを初心者向けにわかりやすく解説します。
この記事は以下のポイントでまとめています。
- 重回帰分析とは?
- 重回帰分析のメリット、デメリット
- 変数の重要度
- 多重共線性
今回は具体的な重回帰分析の実行などは行なっていませんが、以下の記事にてPythonによる重回帰分析の実装を行なっていますので、興味がある方はご参考にしていただければと思います。
では詳細について説明していきます。
重回帰分析とは?
まず、重回帰分析とは何かについて説明します。
重回帰分析は、統計学や機械学習の中でもよく用いられる分析手法の一つです。主に、複数の説明変数(特徴量)と1つの目的変数(ターゲット)との関係を分析するのに使われます。
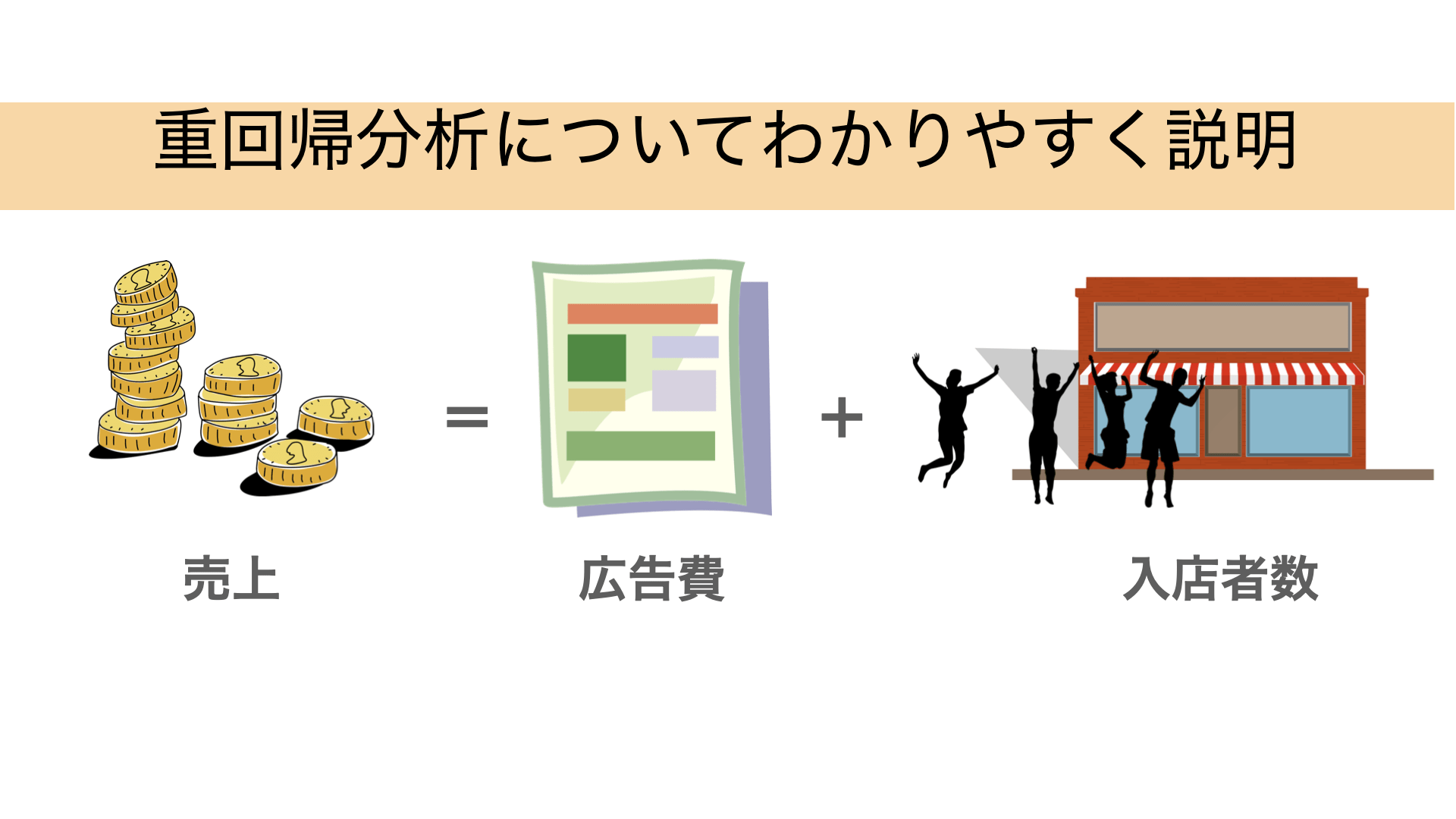
例えば、ある店舗の売上を広告費と入店者数から予測するとします。


■説明変数
- 広告費(円):どれくらい店舗の広告に費用をかけたか
- 入店者数(人):どれくらいの人が店舗に入店したか
■目的変数
- 店舗の売上(円):どれくらい店舗で売上があったか
重回帰分析では、これらのデータを使って、目的変数である「売上」を説明変数である「広告費」「入店者数」から予測することが目的です。
数学的に表現すると、重回帰分析では以下のようなモデルを考えます
売上 = $a_0$ + $a_1$ × 広告費 + $a_2$ × 入店者数
ここで、$a_0$ は切片を表し、$a_1$, $a_2$はそれぞれ回帰係数と呼ばれるもので、変数の相関関係や重要度を把握することができます。
重回帰分析のメリットとデメリット
次に重回帰分析のメリットとデメリットについてご説明します。
まずメリットについてです。
■メリット
次にデメリットについてです。
■デメリット
重回帰分析は複数の説明変数を使用してモデルを構築できるため、予測精度向上や変数の影響度も確認できて便利な手法なのですが、反面で変数を多く採用することによる過学習のリスクや多重共線性のリスクが発生するので要注意ですね。
多重共線性のリスクについては対策法がありますので後ほど解説します。
変数の重要度
次にメリットでも挙げましたが変数の重要度について詳しく説明します。
ここでは冒頭で挙げたように「売上」を「広告費」、「入店者数」で予測するモデルを例として説明します。
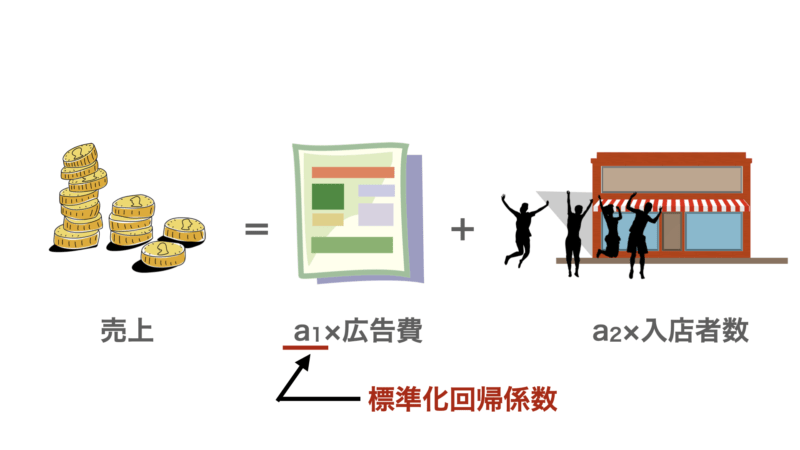

結論から言いますと重回帰分析では標準化回帰係数から変数間の重要度を比較や目的変数との関係性を評価することができます。
標準化回帰係数とは、説明変数と目的変数を標準化した後に求められる回帰係数のことを指します。
標準化とは簡単に言うとスケールを合わせるということです。
具体的には各変数の平均を0、標準偏差を1にするように変換することです。これにより異なる単位の変数間で比較ができるようになります。
逆に標準化せずに「売上」を「広告費」と「入店者数」でモデル構築した場合、広告費が1円増えるのと入店者数が1人増えるのでは同じ1単位増えるだけですが、スケールが全く異なります(そもそも円と人では数値を比較できませんよね)。なので、この1単位のスケールを揃えることを標準化する必要があるのです。
標準化回帰係数を算出したら以下のような観点から評価することができます。
- 係数の絶対値
重回帰分析において、各説明変数の標準化回帰係数の絶対値が変数の重要度を示す指標となります。係数の絶対値が大きいほど、その変数が目的変数に対してより強い影響を持っていることを示します。
- 係数の符号
標準化回帰係数の符号も重要な情報となります。正の係数は、説明変数と目的変数が正の相関関係を持っていることを示します。つまり、説明変数が増加すると目的変数も増加する関係です。一方、負の回帰係数は逆の関係を示します。
多重共線性
最後に重回帰分析のデメリットでも挙げた多重共線性についてご説明します。
多重共線性(Multicollinearity)とは、重回帰分析などの回帰モデルにおいて、説明変数同士が強い相関を持つ状態のことを指します。
多重共線性の影響
多重共線性によって具体的に以下のような影響が生じる可能性が高いです。
- 係数の解釈が困難
多重共線性がある場合、各説明変数の回帰係数の解釈が困難になります。例えば、2つの説明変数が強い相関を持つと、どちらか一方を増加させたときに目的変数が増加するという情報を持っているため、回帰係数を個別に解釈することが難しくなります。
- 係数の不安定性
多重共線性があると、小さなデータの変動やサンプリングの変化によって回帰係数が大きく変動する可能性があります。これにより、モデルの安定性が損なわれます。
- 予測の信頼性が低下
多重共線性がある場合、モデルの予測の信頼性が低下する可能性があります。
私も実務で重回帰分析を使用することもありますが、多重共線性には苦しめられています。適切な手法を使って解決することで、より信頼性のあるモデルを構築するようにしましょう。
多重共線性の評価
次に多重共線性があるかをどのように評価するかをご説明します。
多重共線性を評価するために、一般的に以下の方法が使われます。
- 相関係数の確認
説明変数同士の相関を確認することで、多重共線性の兆候を見つけることができます。相関行列を作成し、説明変数間の相関係数を確認します。相関係数が高い(通常0.7以上)説明変数のペアがある場合、多重共線性の可能性が高いです。 - 分散膨張係数(Variance Inflation Factor, VIF)
VIFは、各説明変数を他の説明変数の線形結合として予測するための係数を表します。VIFの値が大きいほど、多重共線性の影響が強いことを示します。一般的な基準として、VIFが5以上(一部の文献では10以上)の変数は多重共線性があるとされます。 - 新しいデータの追加
既存のデータに似たようなデータを追加して回帰係数を計算した場合、著しく係数が変動した場合は多重共線性の疑いがあります。
以上の方法を使って、多重共線性の存在を評価することができます。ただし、どの指標を使うかは場合によって異なる場合があるため、複数の評価指標を併用し、結果を総合的に判断することが重要かと思います。
多重共線性へのアプローチ
最後に多重共線性へのアプローチについて説明します。
やっかいな多重共線性ですが、アプローチ方法もきちんとあります。
具体的には以下のようなものがあります。
- 変数の削除
相関が強い説明変数を削除することで、共線性を解消することができます。ただし、削除する変数が本当に重要な情報を持っている場合は慎重に検討する必要があります。
- 変数の結合
複数の説明変数を結合して新しい変数を作成することで、共線性を減らせることがあります。ただし、新た作成した変数が何を意味しているかなどの解釈には注意が必要です。
- 主成分分析の使用
主成分分析は相関がある変数を一つの変数としてまとめることができるため、多重共線性を解消できることが期待できます。ただし変数や重要度の解釈が難しくなる場合がありますので周囲が必要です。
個人的には重要度の比較がしたいのであれば変数の削除が一番手っ取り早いのかなとは感じています。変数の結合や主成分分析も効果的なのですが、変数の解釈などが難しくなるため、本末転倒感がありますね。
単純に予測などに使用する場合であれば2, 3などの手法は効果的だと感じています。
主成分分析については以下の記事にまとめていますので、興味のある方は参照いただければと思います。
学習ステップをさらに進めたい方へ
重回帰分析の基本的な概念を理解したら、
次は各説明変数がどのように予測に寄与しているのか、仮定(線形性・独立性など)がモデルの振る舞いにどう影響するのかを、仕組みとして整理しておきたいところです。
その理解を深め、次の学習ステップへ進むためのインプットとしておすすめなのが、
『図解即戦力 機械学習&ディープラーニングのしくみと技術がこれ一冊でしっかりわかる教科書』です。
本書は、コード実装を主目的とした実践書ではなく、
重回帰分析を含む機械学習アルゴリズムの構造・考え方・学習の流れを、図解と文章で丁寧に整理する教科書です。
難解な数式や細かな実装に踏み込まず、
「なぜこの係数になるのか」「どのような前提のもとでモデルが成り立っているのか」を概念レベルで理解できる構成になっています。
たとえば重回帰分析についても、
- 各係数が予測値に与える意味
- 多重共線性が推定結果を不安定にする理由
- 過学習や外挿が起こりやすい条件
といった点を、数式やコードを追わずに“仕組みとして”整理できるため、
この先に学ぶ正則化(Lasso・Ridge)や、より柔軟な回帰モデルへの理解がスムーズにつながります。
「重回帰分析を使ってはいるが、結果をどう解釈すべきか説明しきれない」
「次は正則化回帰や非線形モデルに進みたいので、その前に基礎を整理しておきたい」
そんな方にとって、実装フェーズへ進む前段階のインプットとして最適な一冊です。
本書で理解の土台を固めてから実装に取り組むことで、
“当てはめるだけ”から“前提と限界を意識して使う”へと学習を一段前に進められます。
一方で「Pythonはこれから…」「数式で挫折したことがある…」という方もいらっしゃるかと思います。
そんな初学者の方でもpythonで機械学習を実装できるようになるためのロードマップとオススメの教材について以下の記事にまとめていますので、興味のある方はご覧になって下さい。
終わりに
以上が重回帰分析についての解説になります。重回帰分析は手法も簡単で変数の影響度などを比較できるので非常に重宝しているのですが、多重共線性などのトラップを回避しなければいけないので注意が必要ですね。実務だと多重共線性には本当に苦しめられます。
きちんと使用すればすごく便利な分析手法になりますので、注意点を踏まえた上で使いこなしていきましょう!