こんにちは！ぼりたそです！
今回は「ニューラルネットワークってよく聞くけどなに？」、「参考書を読んだけど、難しい数式が多すぎて途中で挫折した…」
そんな方に向けて、この記事では「ニューラルネットワークとは何か？」をやさしく、順を追って説明します！
この記事は以下のトピックでまとめています。
- ニューラルネットワークとは？
- ニューラルネットワークのアルゴリズム
- ニューラルネットワークの種類
- ニューラルネットワークのメリット&デメリット
- Pythonで実行
それでは順に解説していきます。
ニューラルネットワークとは？
「ニューラルネットワーク（NN）」とは、人間の脳の神経細胞（ニューロン）の働きを模した仕組みで、AI（人工知能）の中でも特に重要な技術です。
AIを勉強していると必ずと言っていいほど登場する手法ですね。
NNのイメージとしては、たくさんの「小さな判断装置（＝ニューロン）」がネットワーク状につながっていて、情報を段階的に処理していく仕組みになっています。
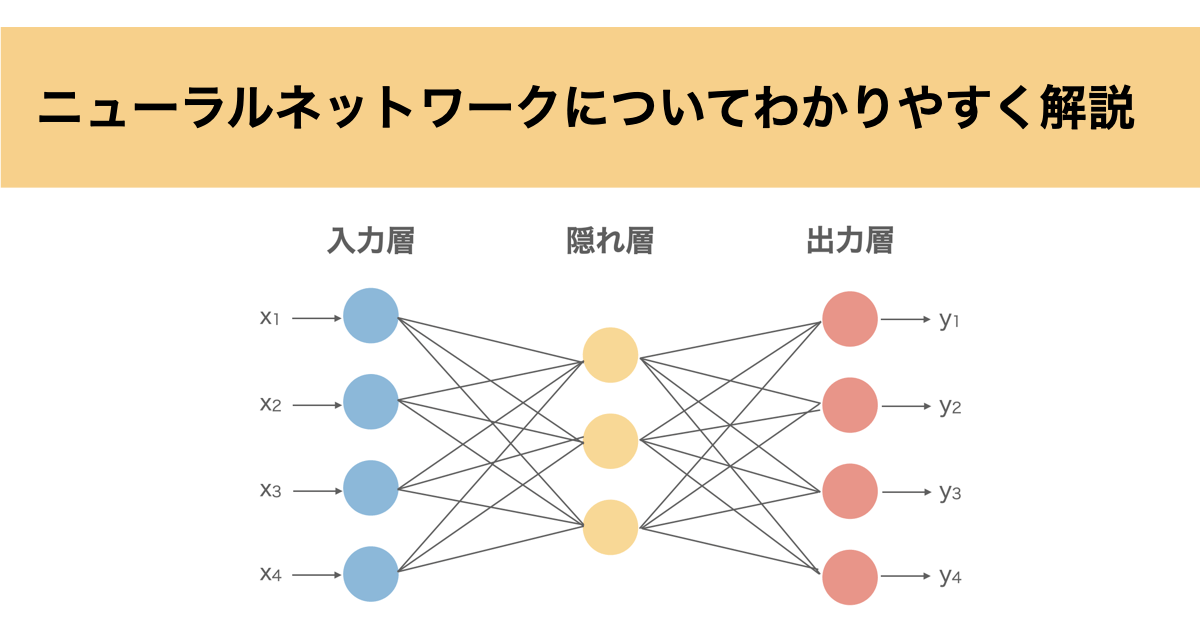
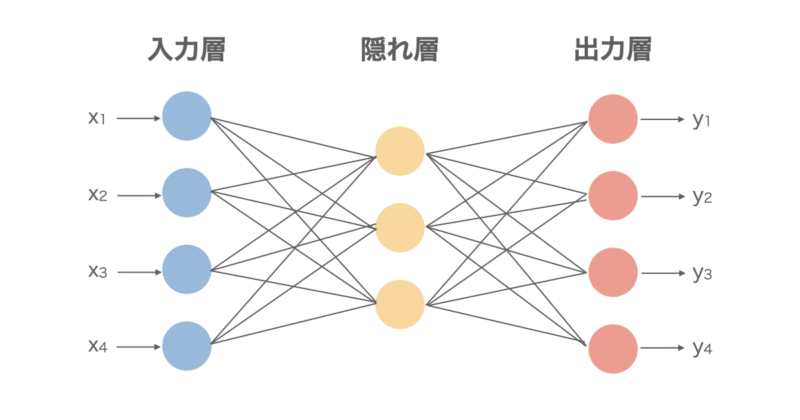
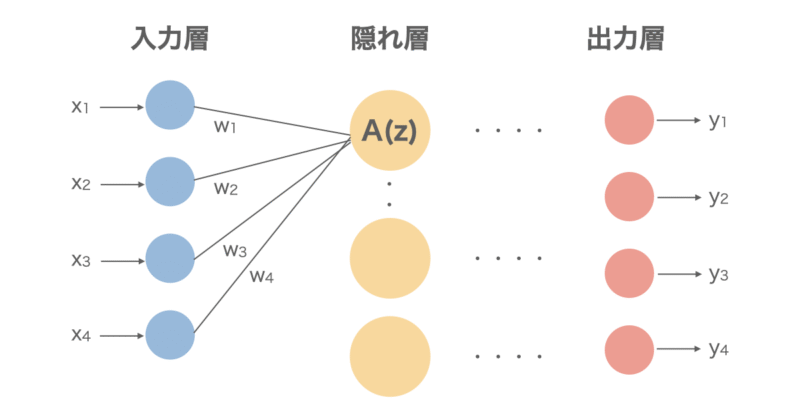
図にすると以下のようになっています。大きく3つの層に分かれており、
- 入力層：データを入力する層（画像データであればピクセルの値）
- 隠れ層：入力したデータを加工、変換する層（画像であれば画像の特徴を捉える層）
- 出力層：結果を出力する層（画像であれば入力された画像が何を表すのかを出力する）
から成り立っています。特に隠れ層が多いNNを深層学習（ディープラーニング）と言います。皆さんも一度は聞いたことがあるのではないでしょうか。
NNは学習モデルが柔軟であるため文字認識や音声認識、画像分類、予測モデルなど、分野を問わず幅広い用途に使用されます。
ニューラルネットワークのアルゴリズム
NNは基本的には以下の工程を何回も繰り返すことで学習を進めていきます。
- 入力データの線形和を計算
- 活性化関数による非線形変換
- 結果を出力&誤差計算
- 誤差逆伝播法による誤差修正
それぞれ順に解説していきます。
入力データの線形和を計算
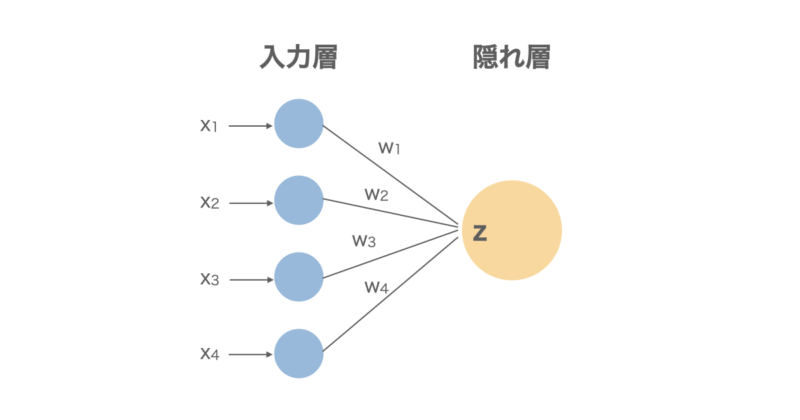
まず、下の図のように入力したデータ $x_i$ に重み係数 $w$ を掛け合わせてバイアス項を足した線形和 $z$ を計算します。これを全てのニューロンで計算します。
バイアス項は線形和の直線の位置を上下にずらすことができ、モデルの表現力を上げるために加えています。
$$z = \sum w_i x_i + b$$
活性化係数による非線形変換
活性化係数とは簡単に言えば入力された情報が重要かどうかを判断するスイッチみたいなものです。
もう少し詳しく説明すると、ニューロンに対して先ほど計算した線形和が入力されたときに、その値をそのまま出力するのではなく、
「この値、大きいから重要っぽいな」
「この値、小さいしノイズっぽいから無視しよう」
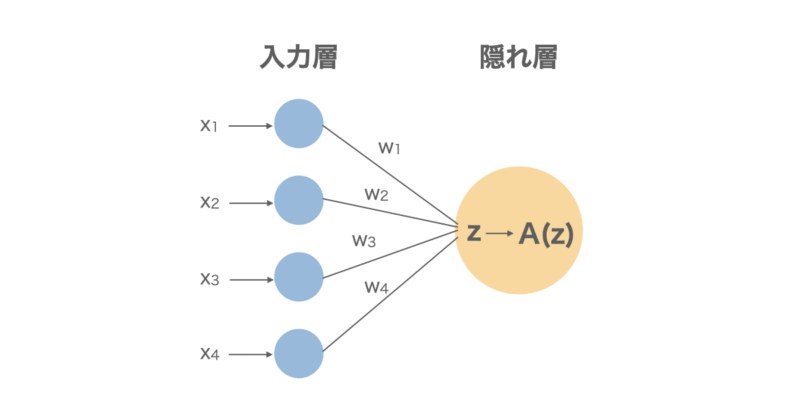
という判断をする関数が「活性化関数」です。下に式も記載します。
$$y = A(z)$$
活性化関数にはいくつか種類があり、よく使用されるものを以下にご紹介します。
- ReLu（Rectified Linear Unit）関数
→0以下の値はバッサリ切り捨て、0より大きい値はそのまま出力する関数。主に隠れ層で使用されることが多いです。
$$A(z) = \max(0, z)$$
- シグモイド関数
→入力値が大きければ1、小さければ0に近づく関数。主に出力層で使用されることが多く、特に分類問題などに使用されます。
$$A(z) = \frac{1}{1 + e^{-z}}$$
- 恒等関数
→入力値をそのまま出力する関数。主に回帰問題の出力層にて使用されることが多いです。
$$A(z) = z$$
- ステップ関数
→入力値が0より小さければ0、0以上であれば1になる関数。あまり柔軟性がないので現在のNNではほぼ使用されていないようです。
$$f(z) =\begin{cases}0 & \text{if } z < 0 \\1 & \text{if } z \geq 0\end{cases}$$
どれも「情報を通す or カットするか」の判断スタイルが違っていて、それぞれ役割があります。
結果出力&誤差計算
入力データから線形和計算→活性化間数による変換により隠れ層を何層も経た末に出力層へ結果が出力されます。
この際、入力したデータに対して出力されたデータにどれだけ誤差があったかを損失関数と使用して計算します。
損失関数はいくつかあり、主に使用されるのは平均二乗誤差（MSE）、二値クロスエントロピー、クロスエントロピーなどが挙げられます。
- 平均二乗誤差
主に回帰モデルに対して使用
$$\mathrm{L} = \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2$$
$y_i$：実際の値
$\hat{y}_i$：予測値
- 二値クロスエントロピー（n個のサンプルに対する平均）
主に二値クラス分類モデルに使用
$$\mathrm{L} = – \frac{1}{n} \sum_{i=1}^{n} \left[ y_i \log(\hat{y}_i) + (1 – y_i) \log(1 – \hat{y}_i) \right]$$
$y_i$：実際の値
$\hat{y}_i$：予測値
- クロスエントロピー（n個のサンプル、C個のクラス分類に対する平均）
主に多クラス分類モデルに使用
$$\mathrm{L} = – \frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{C} y_{ij} \log(\hat{y}_{ij})$$
$y_i$：実際の値
$\hat{y}_i$：予測値
誤差逆伝播法による誤差修正
最後に計算した損失関数から誤差逆伝播法により誤差修正をしていきます。
誤差逆伝播法とは簡単に言うと、出力の誤差をネットワークの各重みにさかのぼって伝え、どこをどれだけ修正すればよいかを計算する仕組みです。
具体的には損失関数の値を小さくするために、各重みをどう修正すべきかを計算します。
そのためにはまず、出力層から入力層へ向かって誤差を逆方向に伝えます。詳しい説明は省きますが、以下に示すような微分（勾配）を使って、各重みに対してどれくらい誤差に影響したかを計算します（チェインルールを使用）。
$$\frac{\partial L}{\partial w} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z} \cdot \frac{\partial z}{\partial w}$$
最終的に誤差に大きく影響した重みとバイアスを以下の更新式に従ってパラメータを最適化していきます。
$$w \leftarrow w – \eta \cdot \frac{\partial L}{\partial w}$$
$ \eta $は学習率を表し、学習率が高く設定すると計算は速いですが最適点を見逃す可能性があり、学習率が低く設定すると計算速度は遅いですが、最適点をきちんと見つけることができます。
以上の流れが一度の学習であり、これを数十回、数百回繰り返すことで学習が完了します。
ニューラルネットワークの種類
ここではNNについて概要を説明しましたが、NNにも用途によって様々な種類が存在します。
基本的なアルゴリズムとしては先ほど説明した流れと同じですが、細かいところで異なってきます。
今回はNNの中でもよく使用される以下の3種をご紹介します。
- 多層パーセプトロン（Multi-Layer Perceptron／MLP）
- 畳み込みニューラルネットワーク（Convolutional Neural Network／CNN）
- 再帰型ニューラルネットワーク（Recurrent Neural Network／RNN）
順に説明していきます。
多層パーセプトロン（Multi-Layer Perceptron／MLP）
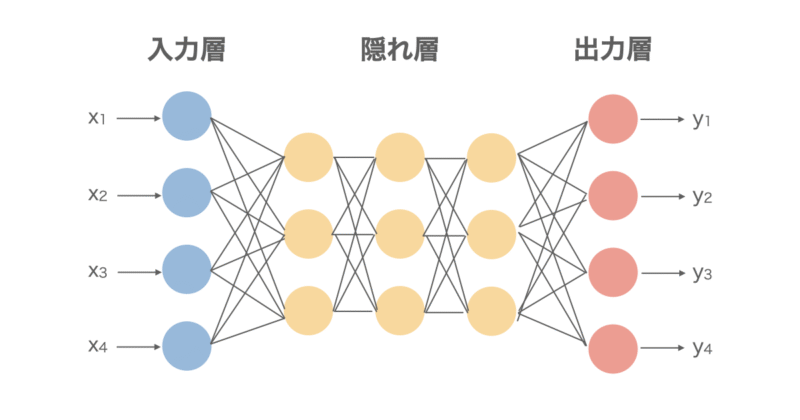
MLPは最も基本的なNNです。入力 → 中間層（隠れ層） → 出力という基本的な全結合型のネットワークであり、各層のすべてのニューロンが次の層とつながっている構造になっています。
用途としては主に回帰や分類用途で使用されることが多いです。
畳み込みニューラルネットワーク（Convolutional Neural Network／CNN）
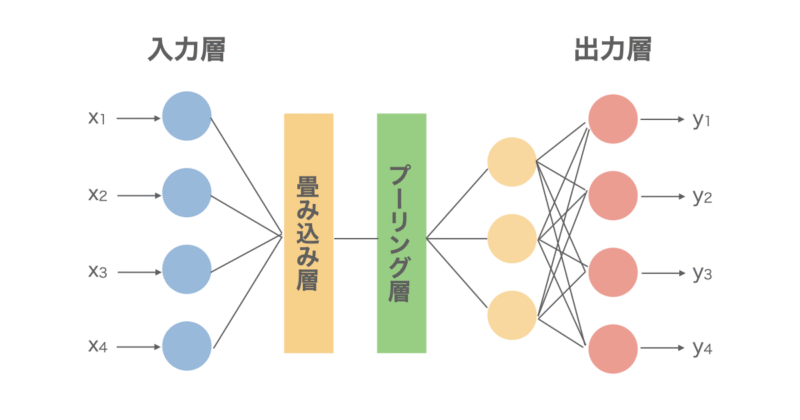
CNNは画像処理に使用される手法であり、入力→畳み込み層→プーリング層→全結合層→出力というネットワークになっています。
ざっくりとしたアルゴリズムとしては以下のようになっています。
- 畳み込み層で「画像の一部のパターン（フィルター）」を抽出
- プーリング層で情報を圧縮（重要な特徴だけ残す）
- 最後はMLPのように全結合して分類する
- 誤差逆伝播でフィルターも学習される
再帰型ニューラルネットワーク（Recurrent Neural Network／RNN）
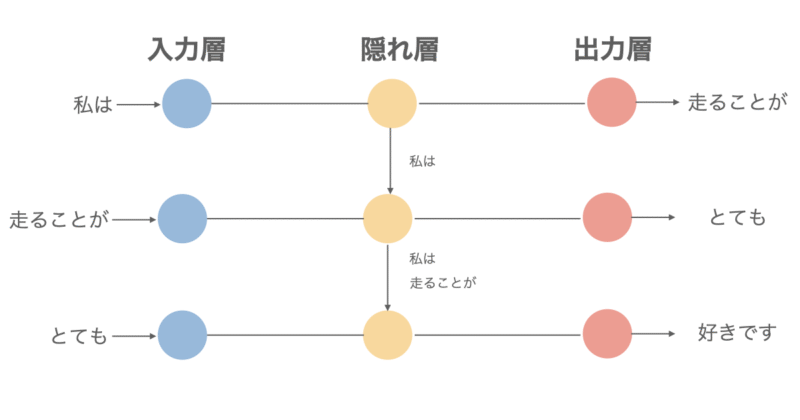
RNNは主に自然言語処理に使用されることが多く、最大の特徴として「入力＋過去の出力」を使って文脈や時系列を考慮できることが挙げられます。
詳細は省きますが、ざっくりとしたアルゴリズムは以下のようになっています。
- 一つ目の入力に対して出力処理を行い、この出力は状態（メモリ）として次のステップに引き継がれる（＝再帰）
- 「二つ目の入力」＋「前回の状態（メモリ）」を元に出力を決定
- これを繰り返して全ての入力データに対して処理を行う
- 誤差は「時系列をさかのぼって」伝播される（BPTT: Backpropagation Through Time）
Pythonで実行
では、実際にPythonでNNを実行してみます。
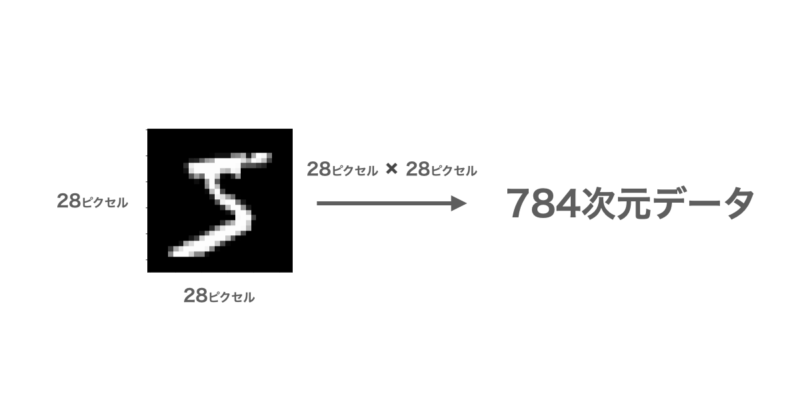
今回はMNISTと呼ばれる0~9の手書き数字データを学習用に60,000件用意してNNを構築し、テスト用に10,000件のデータから予測精度を評価していきます。
MNISTは28×28の784ピクセルから構成される画像データとなっています。
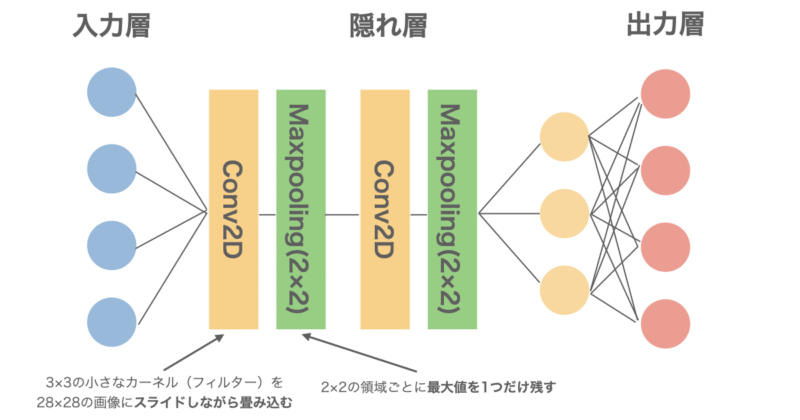
今回はCNN（畳み込みニューラルネットワーク）を使用しており、以下のような構造になっています。最終的な出力は0~9の10個の数字に対する確率であり、最も確率の高い数字を予測値としています。
実際に使用したPythonコードは以下の通りとなっています。
import tensorflow as tf
from tensorflow.keras import layers, models
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
import numpy as np
# 1. データの読み込み
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# 2. データの整形と正規化
x_train = x_train.reshape(-1, 28, 28, 1).astype("float32") / 255.0
x_test = x_test.reshape(-1, 28, 28, 1).astype("float32") / 255.0
# 3. CNNモデルの構築
model = models.Sequential([
layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
layers.MaxPooling2D((2, 2)),
layers.Conv2D(64, (3, 3), activation='relu'),
layers.MaxPooling2D((2, 2)),
layers.Flatten(),
layers.Dense(64, activation='relu'),
layers.Dense(10, activation='softmax') # 出力：10クラス
])
# 4. コンパイル
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# 5. 学習
history = model.fit(x_train, y_train, epochs=5, batch_size=64, validation_split=0.1)
# 6. 評価（Kerasでの評価）
test_loss, test_acc = model.evaluate(x_test, y_test)
print(f"\nKeras Evaluated Test Accuracy: {test_acc:.4f}")
# 7. モデルによる予測
y_pred_probs = model.predict(x_test) # 各クラスの確率
y_pred = np.argmax(y_pred_probs, axis=1) # 最も確率の高いクラスを選択
# 8. 正答率を計算
sklearn_accuracy = accuracy_score(y_test, y_pred)
print(f"Scikit-learn Accuracy Score: {sklearn_accuracy:.4f}")
# 9. 混同行列の出力
print("\nConfusion Matrix:")
print(confusion_matrix(y_test, y_pred))
# 10. 詳細なレポート
print("\nClassification Report:")
print(classification_report(y_test, y_pred))
# 11. 学習曲線の表示
plt.plot(history.history['accuracy'], label='Train Acc')
plt.plot(history.history['val_accuracy'], label='Val Acc')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()
plt.grid(True)
plt.show()
上記コードを実行した結果、予測用データ10000件の正答率は98%となりました。かなり精度の良いNNが構築できたと言えます。
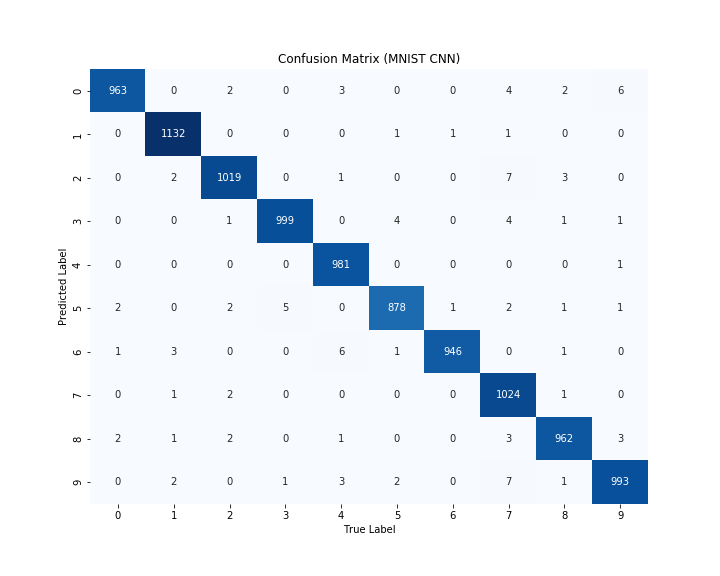
もう少し詳細に結果を見るために予測と正解値の混同行列をヒートマップで確認してみます。縦軸が予測した数字であり、横軸が実際の数字になります。
体格成分が正解数になっており、どの予測もほとんど正解していることがわかります。
以上がPythonを使用したNNの実装になります。
終わりに
以上がニューラルネットワーク（NN）について簡単な説明となります。NNはパラメータの調整や隠れ層によっていくつもの種類があるので、より詳しい説明が知りたい場合は文献を参考にしていただければと思います。この記事が少しでも皆様の理解の一助になれば嬉しいです。
