こんにちは!ぼりたそです!
今回は機械学習モデルにおける特徴量と目的変数の関係を可視化できるPD(Partial Dependence)について解説した記事を作成しました。
この記事は以下のポイントでまとめています。
- 特徴量と予測値の関係
- PD(Partial Dependence)について
- 因果関係としての解釈
- 参考書籍
機械学習モデルを解釈する別の手法としてPFI, ICE, SHAPについても過去にまとめていますので、興味のある方は以下の記事を参照いただければと思います。
それでは順に解説していきます。
特徴量と予測値の関係
機械学習モデルを解釈する際に特徴量と予測値の関係は非常に重要になってきます。
例えば、下の図のようにブラックボックスな機械学習モデルに対して、特徴量を増加させると予測値は増えていくのか減っていくのか、線形なのか非線形なのか、周期的か断続的かなどを知ることは機械学習モデルを解釈する際に非常に重要になってきますよね。
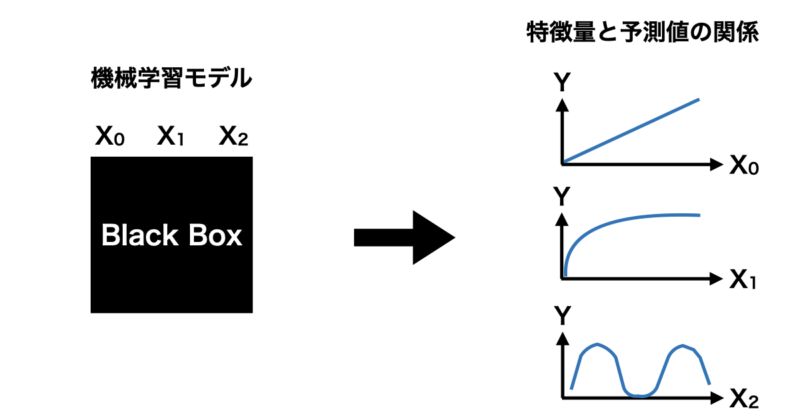

特徴量重要度の算出も解釈手法として優れていますが、あくまで特徴量がどの程度機械学習モデルに影響するかを示すもので、特徴量の増減に対して予測値がどのように振る舞うかを知ることはできません。
ここまで、特徴量と予測値の関係についての重要性を説明してきましたが、実際にどのような手法でその関係性を視覚化するかを説明していきます。
PD(Partial Dependence)について
特徴量と予測値の関係を理解する手法としてPD(Partial Dependence)について紹介していきます。
PDとは一言で説明すると「興味のある特徴量を動かし、他の特徴量を固定することで各インスタンス(個別データ)の予測値を平均して可視化する」手法です。
例えば、 $f(X_0, X_1, X_2)$ で表すことのできるモデルを構築した時、 $X_0$ と予測値の関係を可視化したいとします。
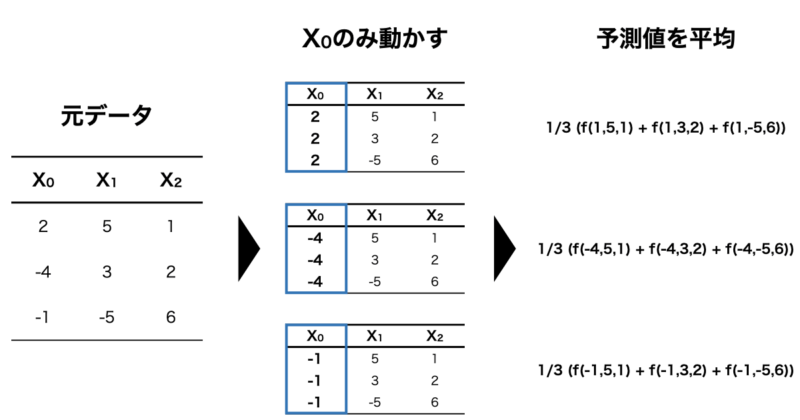
その場合、下の図のように $X_1, X_2$ の値は固定し、 $X_0$ の値のみを動かして予測値を算出します。
さらに、算出した予測値をインスタンスごとに平均化することで $X_0$ と予測値の関係を可視化することができるというわけです。

それでは実際にPythonを使用してPDを実行してみましょう。
今回は例として $X = (X_0, X_1, X_2)$ とした時、以下の $f(X)$ に従うデータを生成してPDを実行してみます。
$$f(X) = X_0 + \exp (- X_1 ) + sin( X_2 )$$
また、今回の機械学習モデルはランダムフォレストを使用し、説明変数は-5 ~ 5の範囲でデータを生成しています。
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.inspection import partial_dependence, PartialDependenceDisplay
import matplotlib.pyplot as plt
# データ生成
np.random.seed(42)
n_samples = 1000
X0 = np.random.uniform(-5, 5, n_samples)
X1 = np.random.uniform(-5, 5, n_samples)
X2 = np.random.uniform(-5, 5, n_samples)
y = X0 + np.exp(-X1) + np.sin(X2) + np.random.normal(0, 0.1, n_samples) # ノイズを追加
# DataFrame作成
X = pd.DataFrame({'X0': X0, 'X1': X1, 'X2': X2})
# ランダムフォレストモデルの構築
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X, y)
# absモデルのR2値を算出
y_pred = model.predict(X)
r2 = r2_score(y, y_pred)
print(f'Model R2 score: {r2:.4f}')
# Partial Dependence Plot
features = [0, 1, 2] # X0, X1, X2を指定
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
# 各特徴量ごとにPDプロットを描画
for i, feature in enumerate(features):
display = PartialDependenceDisplay.from_estimator(
model, X, [feature], ax=axes[i], line_kw={"color": "blue"}
)
axes[i].set_title(f'Partial Dependence Plot for X{feature}')
plt.suptitle("Partial Dependence Plots for Each Feature", fontsize=16)
plt.tight_layout()
plt.subplots_adjust(top=0.85)
plt.show()
#Model R2 score: 0.9998コードの実行結果として、まずは学習モデルの $R^2$ 値が1.0 となっており、きちんと学習できていることがわかります。
PDの実行結果は以下の通りです。左から $X_0, X_1, X_2$ となっており、生成元になった関数である$f(X) = X_0 + \exp ( X_1 ) + sin( X_2 )$からきちんと各特徴量と予測値の関係が可視化されていることがわかると思います。
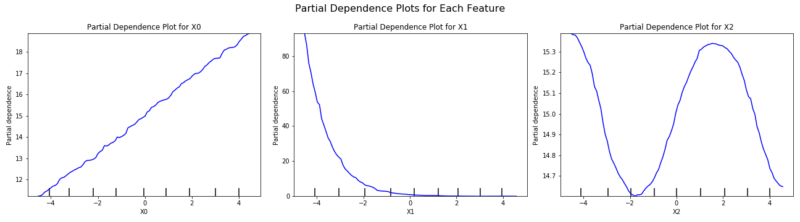

また、PDについて特徴量と目的変数の散布図と変わらないのでは?と思う方もいるかと思いますが、PDは全ての特徴量を考慮した上である特徴量と予測値の関係を可視化しているので、ただの特徴量VS目的変数の散布図とは全く異なります。
因果関係としての解釈
続いて、PDにより特徴量と予測値の関係が可視化できた際にそれを因果関係として解釈しても良いかという点について説明していきます。
結論、PDにより算出した特徴量と予測値の関係をそのまま因果関係として捉えるのはリスクが高いです。
理由としては偽相関の恐れがあるためです。
下の図のように目的変数 $Y$ 対して因果関係にある特徴量 $X_0$ があるとします。さらにこの $X_0$ と強く相関を持つ $X_1$ があるとします。なお、 $X_1$ と $Y$ の間には因果関係は全くないとします。
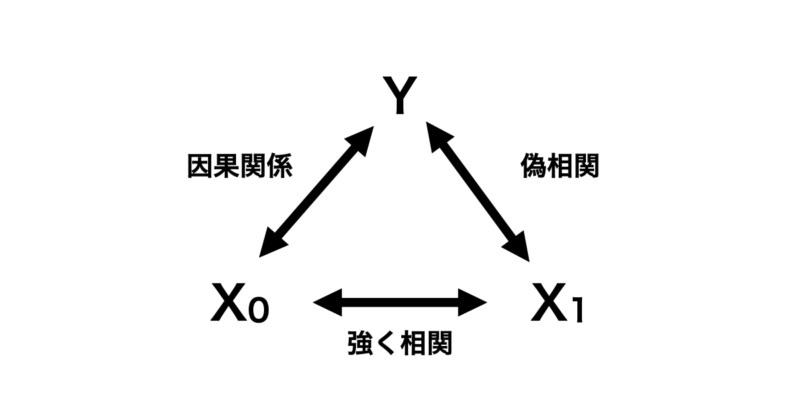

この場合、PDの性質上 $X_0$ が学習モデルに入っていればいいですが、 $X_1$ のみ学習モデルに入れている場合は最悪のパターンです。全く因果関係がない特徴量と目的変数をあたかも因果関係があるように解釈してしまう恐れがあるからです。
なので、PDによる特徴量と予測値の関係が可視化できたからといって容易に特徴量を因果関係と結びつけるのではなく、あくまで特徴量と目的変数の因果関係を立証する仮説として考えた方が良いです。
また、PDの結果を単純に「特徴量に対する予測値の平均的な関係」として捉える分には問題なく、因果関係ではなくモデルの振る舞いとして解釈するのが安全な利用方法と言えます。
参考書籍
本記事を作成するにあたり参考にさせていただいた書籍をご紹介します。
■機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック〜
この書籍は機械学習を解釈する手法としてPFI、PD、ICE、SHAPの大きく4つについて解説している書籍になります。
私が読んだ所感ですが、線形回帰の説明から始まり、機械学習モデルの解釈の必要性や目的に応じた手法が順序立てて説明されており非常に読みやすかったです。
また、簡単なモデルを例としていたため、数学的に躓く箇所もほとんどありませんでした。
さらに、Pythonコードも公開されているので、学んだ内容をすぐに実践できるのもオススメできるポイントです。
もしご興味ある方がいましたら購入を検討されてはいかがでしょうか?
終わりに
以上が機械学習モデルを解釈する手法であるPD(Partial Dependence)についての解説になります。PFIなどの特徴量重要度を算出する手法とは異なり、特徴量と予測値の関係が可視化できるので、特徴量が増減すると目的変数にどのように影響するかが理解できて面白いですね。最後にこの記事がPDないし、機械学習モデルの解釈について学びたい方への一助になれば幸いです。