こんにちは!ぼりたそです!
今回は機械学習モデルを解釈する手法として特徴量(説明変数)の重要度を算出できるPFI(Permutation Feature Importance)を紹介したいと思います。
この記事は以下のポイントでまとめています。
また、機械学習モデルの解釈手法としてPD, ICE, SHAPについてもまとめた記事を作成しましたので、興味のある方は参照ください。
それでは順に解説していきます。
特徴量重要度と機械学習モデルの解釈
まずは特徴量重要度と機械学習モデルの解釈について説明していきます。
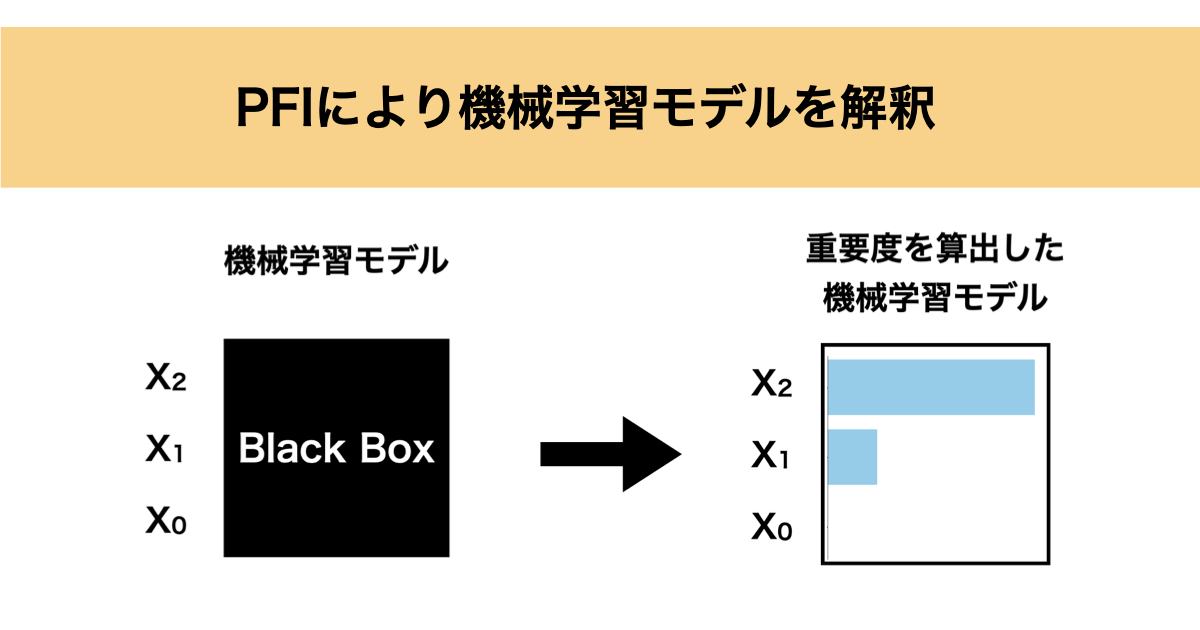
通常、機械学習モデルはブラックボックスモデルになるケースが大半かと思います。学習データから機械学習モデルができて予測精度も良さそうだけど、どの特徴量が影響しているかわからないような状態です。

なので、どの特徴量がどのくらい影響しているのか、特徴量重要度を知ることで少しでも機械学習モデルを解釈したいというモチベーションが湧いてきます。
特徴量重要度がわかれば、どの特徴量を変えるのが一番影響が大きいか良いかわかりますし、ドメイン知識と比較して機械学習モデルが信頼できるか評価することができます。
PFI(Permutation Feature Importance)
さて、ここからは特徴量重要度を算出する手法としてPFIについて解説していきたいと思います。
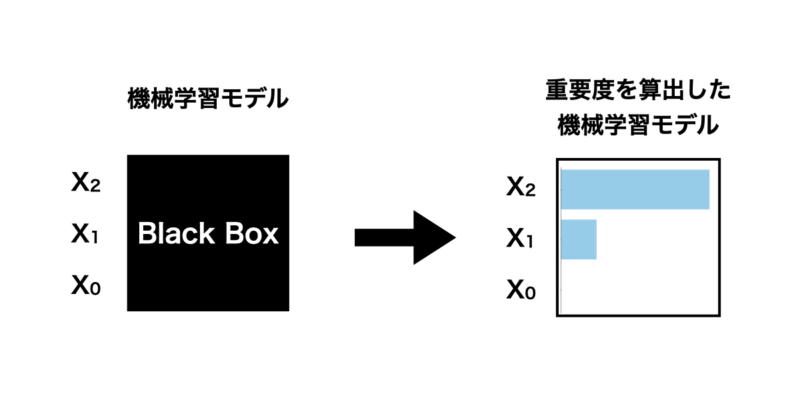
PFIは元のデータに対して特徴量をシャッフルしてその特徴量を使用できない状態にします。その状態で予測モデルを構築し、元データの予測精度と比較することで、その特徴量がどれだけ重要であったかを数値化する手法です。

実際に例を用いて説明していきます。
簡単な例として下のような $X = (X_0, X_1, X_2)$ を特徴量とした線形回帰式に従うデータを取り扱ってみます。
$$Y = 0 \cdot X_0 + 1 \cdot X_1 + 2 \cdot X_2$$
この線形回帰式のデータに対して以下の手順で特徴量重要度を算出します。
- まず、元データについて学習モデルを構築し、テストデータの予測誤差を計算します。
- 次に $X_0$ をシャッフルし、そのデータで予測モデルを構築した後にテストデータの予測誤差を算出します。
- 1の予測誤差に対して 2で算出した予測誤差を比較し、差分や増加率から特徴量重要度を計算する。
- $X_1$, $X_2$ も同様に1-3の手順を繰り返す。
実際にPythonを使用して算出してみます。
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.inspection import permutation_importance
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# 1. データ生成
np.random.seed(0)
n_samples = 100
X = np.random.rand(n_samples, 3)
y = 0 * X[:, 0] + 1 * X[:, 1] + 2 * X[:, 2] # f(x) = 0X_0 + 1X_1 + 2X_2
# 2. 学習データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 3. データの標準化(学習データに基づいて標準化)
scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.transform(X_test)
# 4. モデルの学習
model = LinearRegression()
model.fit(X_train_std, y_train)
# 5. テストデータを用いた PFI による特徴量重要度の計算
result = permutation_importance(model, X_test_std, y_test, n_repeats=30, random_state=0)
importance = result.importances_mean
# 6. 結果の可視化
feature_names = ['X_0', 'X_1', 'X_2']
importance_df = pd.DataFrame(importance, index=feature_names, columns=['Importance'])
importance_df.sort_values(by="Importance", ascending=True, inplace=True)
plt.figure(figsize=(8, 5))
plt.barh(importance_df.index, importance_df['Importance'], color='skyblue')
plt.xlabel("Feature Importance (PFI)")
plt.ylabel("Features")
plt.title("Permutation Feature Importance")
plt.show()
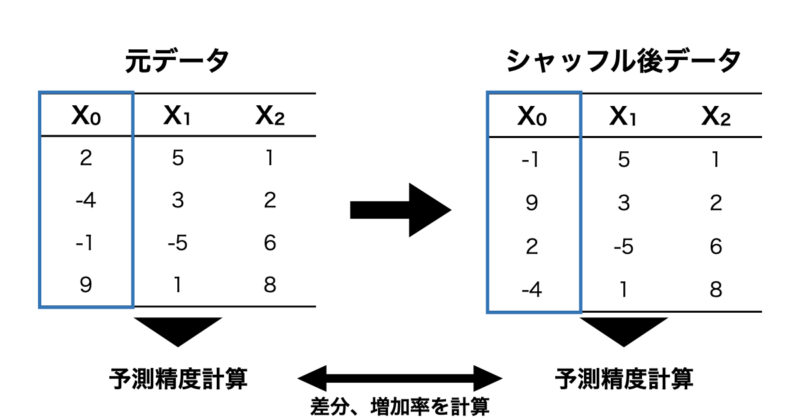
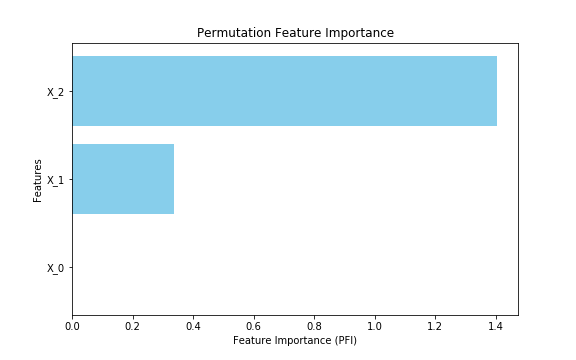
上記コードを実行すると以下のように特徴量重要度が計算されました。 $X_2$ が最も重要度が高く、次いで $X_1$ 、 $X_0$ は重要度がほぼ0になっています。元にした線形回帰の式からも妥当な結果であることがわかります。

GPFI(Grouped Permutation Feature Importance)
次にPFIの派生的な手法としてGPFIについて説明していきます。
GPFIは強い相関のある特徴量同士をグループ化してPFIを実行する手法となります。
これは、相関のある特徴量を別にしてしまうと重要度が分散してしまい、影響が低く見積もられてしまうことを防ぐための手法となります。
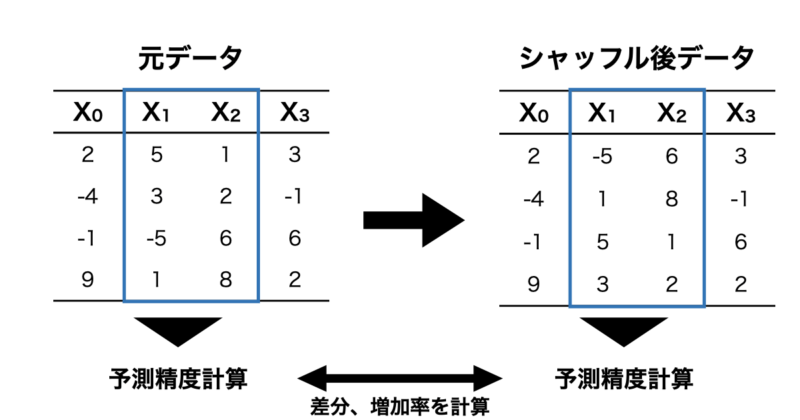

こちらも例を用いて説明していきます。
例として下のような$X = (X_0, X_1, X_2, X_3)$を特徴量とした線形回帰式に従うデータを取り扱ってみます。
$$Y = 0 \cdot X_0 + 1 \cdot X_1 + 2 \cdot X_2 + 3 \cdot X_3$$
この時、 $X_1, X_2$ は強い相関があるとします。
この線形回帰式のデータに対して以下の手順で特徴量重要度を算出します。
- まず、元データについて学習モデルを構築し、テストデータの予測誤差を計算します。
- 次に $X_1, X_2$ をグループ化した状態でシャッフルし、そのデータで予測モデルを構築した後にテストデータの予測誤差を算出します。
- 1の予測誤差に対して 2で算出した予測誤差を比較し、差分や増加率から特徴量重要度を計算する。
- $X_0$, $X_3$ も同様に1-3の手順を繰り返す。
実際にPythonを使用して算出してみます。
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# 1. データ生成
np.random.seed(0)
n_samples = 100
X_0 = np.random.rand(n_samples)
X_1 = np.random.rand(n_samples)
X_2 = X_1 + np.random.normal(0, 0.01, n_samples) # X_1とX_2を強く相関させる
X_3 = np.random.rand(n_samples)
X = np.column_stack((X_0, X_1, X_2, X_3))
y = 0 * X[:, 0] + 1 * X[:, 1] + 2 * X[:, 2] + 3 * X[:, 3] # f(x) = 0X_0 + 1X_1 + 2X_2 + 3X_3
# 2. 学習データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 3. データの標準化(学習データに基づいて標準化)
scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.transform(X_test)
# 4. モデルの学習
model = LinearRegression()
model.fit(X_train_std, y_train)
# 5. GPFIの計算
# グループを定義 (X_1, X_2をグループ化)
groups = {
"Group_1 (X_1, X_2)": [1, 2], # インデックス1と2をグループ化
"X_0": [0],
"X_3": [3]
}
# ベースライン誤差の計算
baseline_mse = mean_squared_error(y_test, model.predict(X_test_std))
# グループごとにシャッフルして重要度を計算
importances = {}
for group_name, indices in groups.items():
X_test_permuted = X_test_std.copy()
for index in indices:
np.random.shuffle(X_test_permuted[:, index]) # 特定のグループ内の特徴量をシャッフル
permuted_mse = mean_squared_error(y_test, model.predict(X_test_permuted))
importances[group_name] = permuted_mse - baseline_mse # 誤差の増加分
# 6. 結果の可視化
importance_df = pd.DataFrame(list(importances.items()), columns=["Feature Group", "Importance"])
importance_df.sort_values(by="Importance", ascending=True, inplace=True)
plt.figure(figsize=(8, 5))
plt.barh(importance_df["Feature Group"], importance_df["Importance"], color="skyblue")
plt.xlabel("Feature Importance (GPFI)")
plt.ylabel("Feature Groups")
plt.title("Grouped Permutation Feature Importance")
plt.show()
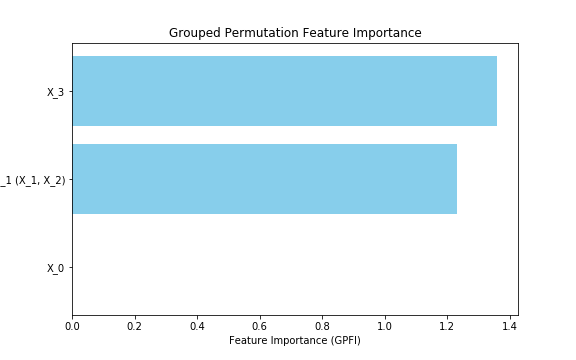
実行した結果、重要度は以下の通りとなりました。 $X_3$ が最も重要度が大きいですが、 $X_1, X_2$ のグループも同程度となりました。元のデータの編回帰係数からも妥当な結果となっていることがわかります。

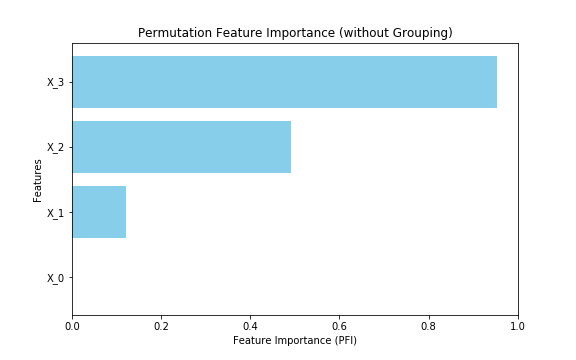
ちなみにグループ化せずにPFIを実行すると以下のような結果になります。 最も重要度が大きい$X_3$ に対して $X_1, X_2$ は小さく、足し合わせても $X_3$ の半分程度しかありません。この結果からもGPFIの有用性がわかるかと思います。

特徴量重要度と因果関係
最後に特徴量重要度と因果関係について説明します。
結論、PFIにより算出した特徴量重要度を因果関係として捉えるのはリスクが高いです。
理由としては偽相関の恐れがあるためです。
下の図のように目的変数 $Y$ 対して因果関係にある特徴量 $X_0$ があるとします。さらにこの $X_0$ と強く相関を持つ $X_1$ があるとします。なお、 $X_1$ と $Y$ の間には因果関係は全くないとします。
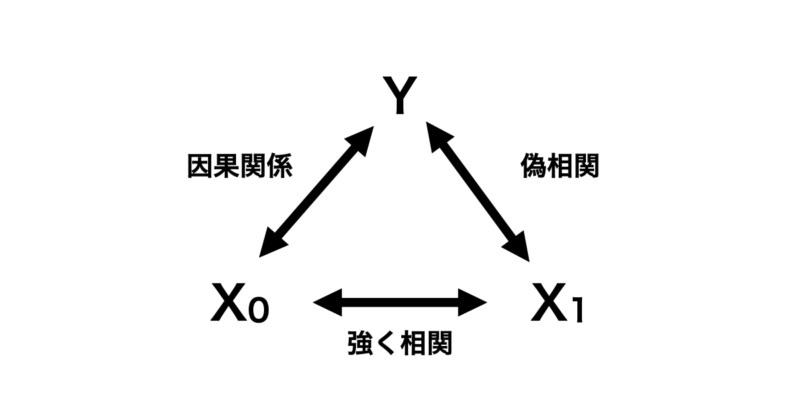

この場合、 $X_0$ が学習モデルに入っていればいいですが、 $X_1$ のみ学習モデルに入れている場合は最悪のパターンです。全く因果関係がない特徴量と目的変数をあたかも因果関係があるように解釈してしまう恐れがあるからです。
なので、PFIにより算出した重要度が高いからといって容易に特徴量を因果関係と結びつけるのではなく、その特徴量をさらに深掘りして因果関係を考える必要があります。
参考書籍
本記事を作成するにあたり参考にさせていただいた書籍をご紹介します。
■機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック〜
この書籍は機械学習を解釈する手法としてPFI、PD、ICE、SHAPの大きく4つについて解説している書籍になります。
私が読んだ所感ですが、線形回帰の説明から始まり、機械学習モデルの解釈の必要性や目的に応じた手法が順序立てて説明されており非常に読みやすかったです。
また、簡単なモデルを例としていたため、数学的に躓く箇所もほとんどありませんでした。
さらに、Pythonコードも公開されているので、学んだ内容をすぐに実践できるのもオススメできるポイントです。
もしご興味ある方がいましたら購入を検討されてはいかがでしょうか?
終わりに
以上がPFIによる機械学習モデルの解釈に関する解説でした。機械学習を解釈する手法は多くあり、また別の機会にまとめたいと思っています。以上、簡単ではありますが、機械学習モデルの解釈に困っている方の一助になれば幸いです。