こんにちは！ぼりたそです！
今回はサポートベクターマシン（SVM）について初学者の方でも理解しやすいように解説してみました。
この記事は以下のポイントでまとめています。
- サポートベクターマシン（SVM）とは
- サポートベクターマシン（SVM）のアルゴリズム
- PythonでSVMを実行
- 非線形問題への適用
また、SVMの原理を利用した回帰手法であるサポートベクター回帰（SVR）について、まとめた記事を作成しましたので、興味のある方は参照いただければと思います。
それでは順に解説していきます。
サポートベクターマシンとは？
サポートベクターマシン（SVM）は、機械学習のアルゴリズムの一種で、主に二値分類問題に使われます。かなりざっくり言うと、SVMはデータを分ける「境界線」を探し出す方法です。
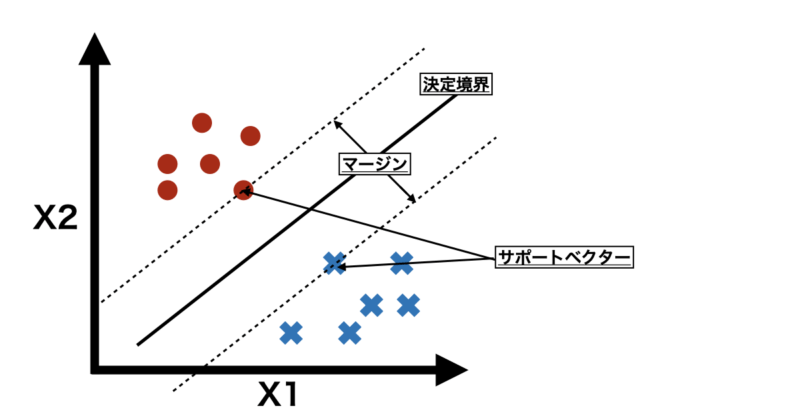
SVMは、異なるクラスのデータ点から最も離れた線（高次元の場合は超平面）を見つけることで、データを分類します。この「距離」をマージンと呼び、SVMはマージンが最大になるような決定境界を探します。これにより、新しいデータがどちらのクラスに属するかを予測しやすくなります。
ちなみに、「サポートベクター」とは、決定境界に最も近いデータ点のことを指します。これらの点が決定境界を定める役割を果たしており、境界を調整するために重要なポイントとなります。
また、以下にSVMのメリット、デメリットを記載します。
■メリット
■デメリット
SVMのアルゴリズム
次にSVMのアルゴリズムについて説明していきます。
ざっくりと言えば、SVMは決定境界とマージンを決めてしまえば終わりです。
それを踏まえると大きく2つ〜3つのプロセスに分けることができます。
- 決定境界とマージンの定義
- スラッグ変数の導入
- 最適化関数の導入
それぞれ順に説明していきます。
決定境界とマージンの定義
まずは決定境界とマージンについて定義していきます。
下に例として変数が2つでクラス+1（●）に属するグループとクラス-1（✖︎）に属するグループがあったとします。
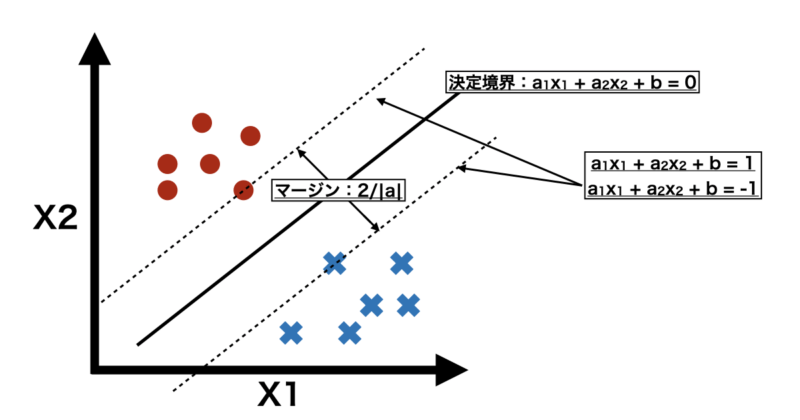
この時、クラス+1と-1を適切に分ける決定境界は以下の式で表すことができます。
$$f(x_i) = a_1 \cdot x_1 + a_2 \cdot x_2 + b = 0$$
$a_i$ は各説明変数の重み
$b$ は定数項
を表しています。この $a_i$ , $b$ を求めることがSVMの命題となります。
また、決定境界から最も近いサンプルの距離が同じになるように線を引きます。この時、各直線は以下のような式で表すことができます。この時、bを定数倍することで直線を並行移動しています。
$$a_1 \cdot x_1 + a_2 \cdot x_2 + b = 1$$
$$a_1 \cdot x_1 + a_2 \cdot x_2 + b = -1$$
また、上記2つの直線の距離をマージンと呼び、以下の式で表すことができます。
$$\text{マージンの幅} = 2 \times \frac{|a_1 \cdot x_1 + a_2 \cdot x_2 + b|}{\sqrt{{{a_1}^2}+{a_2}^2}} = \frac{2}{\sqrt{{{a_1}^2}+{a_2}^2}} = \frac{2}{|a|}$$
$a_1 \cdot x_1 + a_2 \cdot x_2 + b$ が+1, -1を通ることから $|a_1 \cdot x_1 + a_2 \cdot x_2 + b| = 1$ として計算しています。
このマージンを最大化するように $a_i$ , $b$ を求めればいいいのですが、実際は正しく判別できないサンプルもあります。その場合は損失関数としてスラッグ関数を導入する必要があります。
スラッグ変数の導入
スラッグ変数 $\xi$ は損失関数（ペナルティ）であり、下図のように
正しく分類されマージンの境界上、外側にあるサンプルは $\xi = 0$
それ以外のサンプルは $\xi = |y_i – f(x_i)|$
と定義されます。
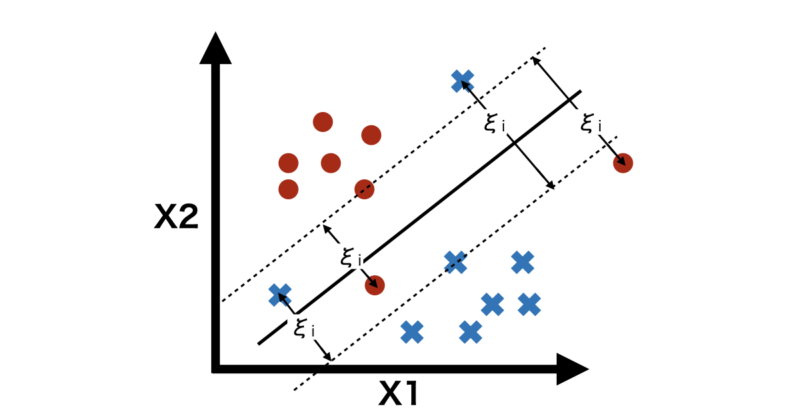
各サンプルのスラッグ変数の和である、
$$\sum_{j=1}^{N} \xi_j$$
として、これを最小化するように $a_i$ , $b$ を求める必要があります。
最適化関数の導入
以上からSVMはマージンを最大化し、スラッグ変数を最小化するように $a_i$ , $b$ を求めることで最適な決定境界を引くことができます。
そのために以下の最適化関数 $S$ を定義します。SVMではこの $S$ の最小化を目指します。
$$ S = \frac{1}{2} |a|^2 + C \sum_{i=1}^{N} \xi_i $$
第一項はマージンを表す項になっており、 $S$ を最小化問題にするためにマージン$\frac{2}{|a|}$ に対して逆数を取ります。また、詳細は省きますが、最適化のしやすさから $|a|$ を二乗しています。
第二項 はスラッグ変数を表しており、 $C$ はハイパーパラメータとなっています。 $C$ が大きければそれだけ誤分類が無いように最適化され、 $C$ が小さければマージンが大きくなるように最適化されます。
この最適化関数を解くにはラグランジュの未定乗数法を使用するのですが、今回は解法については割愛させていただいます。
以上の手法により、SVMは決定境界及びマージンを設定することができ、分類問題を解くことができます。
Pythonで実装
それでは実際にPythonでSVMを実行してみましょう。
今回は以下のような条件でSVMを実行しています。
| 条件 | 説明 |
|---|---|
| 学習データ | ランダム関数を使用して生成しています |
| 説明変数 | 説明変数の個数は2つとしています |
| 目的変数 | 1, -1の二値としています |
| ハイパーパラメータ $C$ | グリッドサーチで最適化しています |
実際のコードが以下のようになっています。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import make_blobs
# データを生成
np.random.seed(42)
X, y = make_blobs(n_samples=100, centers=2, cluster_std=1.5, n_features=2, random_state=42)
# クラスラベルを-1, 1に変換
y = np.where(y == 0, -1, 1)
# 他のクラスに混ざるように外れ値を追加
n_outliers = 5
np.random.seed(0)
outliers = np.random.uniform(low=X.min(axis=0), high=X.max(axis=0), size=(n_outliers, 2))
outlier_labels = np.random.choice([-1, 1], size=n_outliers)
X = np.vstack([X, outliers])
y = np.concatenate([y, outlier_labels])
# ハイパーパラメータCのグリッドサーチ
param_grid = {'C': [0.01, 0.1, 1, 10, 100, 1000]}
grid_search = GridSearchCV(SVC(kernel='linear'), param_grid, cv=5)
grid_search.fit(X, y)
# 最適なモデルを取得
best_model = grid_search.best_estimator_
# サポートベクター、決定境界を描画
def plot_decision_boundary(clf, X, y):
# 描画範囲の設定
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
# モデルの予測値を取得
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 決定境界とマージンの描画
plt.contour(xx, yy, Z, levels=[-1, 0, 1], linestyles=['--', '-', '--'], colors='k')
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100, facecolors='none', edgecolors='k')
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.bwr, edgecolors='k')
plt.title(f'Soft Margin SVM with Linear Kernel (C = {clf.C})')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
# 最適なモデルを用いて決定境界をプロット
plot_decision_boundary(best_model, X, y)
# 最適なパラメータの出力
print(f"Best parameter (C): {grid_search.best_params_['C']}")
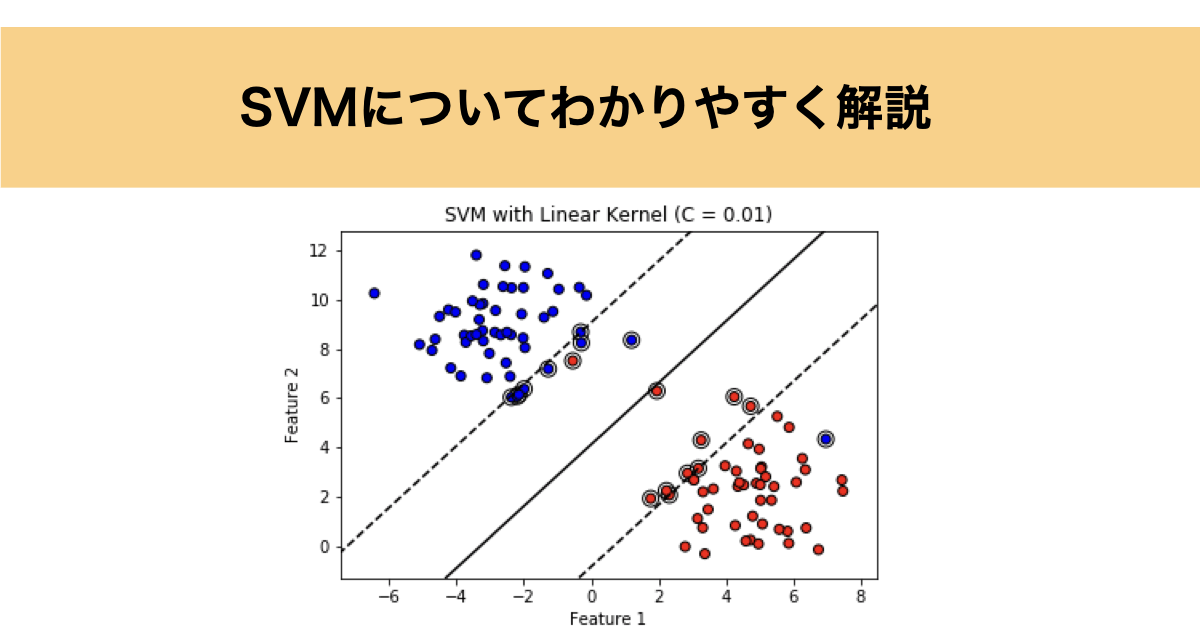
結果は以下のように出力されました。黒線が決定境界で点線がサポートベクター上の線、丸で囲っているサンプルはサポートベクターとなっています。
外れ値を忍ばしておきましたが、きちんとマージンを最大化しつつ決定境界を引けているようです。
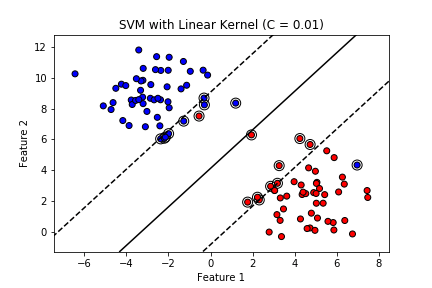
以上がPythonで実際にSVMを実行した結果になります。
非線形問題への適応
ここまでSVMの基礎的な原理について説明しましたが、最後に発展として非線形問題への適応についてご紹介します。
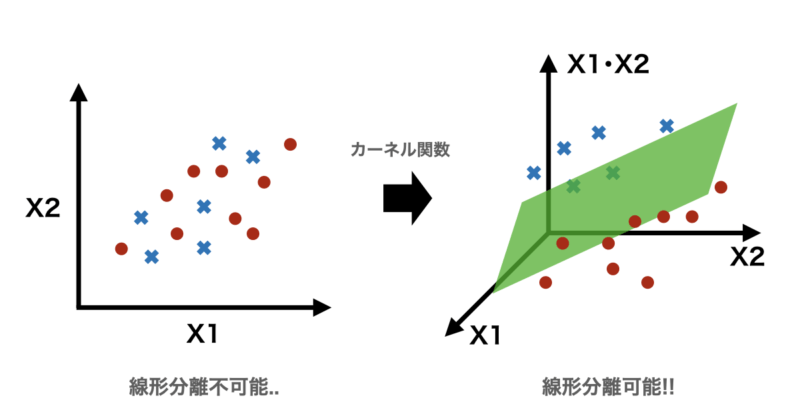
下に例として変数が2つでクラス+1（●）に属するグループとクラス-1（✖︎）に属するグループがあったとします。
直感的に先ほどのようは線形分離はできない気がします。
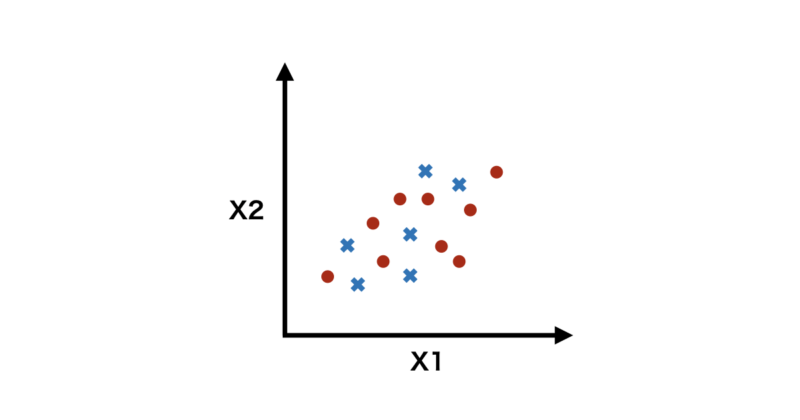
非線形変換
そこで非線形変換という手法を導入します。
非線形変換は現在の特徴量を変換して、より高次元空間へ変換することで線形分離を可能にするための手法です。
具体的には入力データを高次元空間にマッピングする操作を数式で表現し、元の空間では線形に分離できないデータを高次元空間に写すと線形に分離可能となることが期待できます。
先ほどの例で表すと二次元上では線形分離できなかったものが、非線形変換を使用して内積であるX1･X2を3次元に加え、新しい空間へ変換することで、緑色のハイパープレーン（超平面）で線形分離が可能になるということです。
式で表すと以下の通りとなります。
$$\mathbf{x} = (X1, X2) \mapsto \phi(\mathbf{x}) = (X1, X2, X1 \cdot X2)$$
非線形変換の弱点
しかし、非線形変換にも弱点が存在し、それが計算コストが高いということです。
例えば、以下のように$ x $が変換関数$ \phi(\mathbf{x}) $により高次元へ変換されたとします。
$$\mathbf{x} \mapsto \phi(\mathbf{x})$$
この時、高次元空間におけるデータを線形分離するために以下のラグランジュ乗数を用いた最適化問題を解く必要があります。
$$\max_{\boldsymbol{\alpha}} \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j \phi(\mathbf{x}_i)^\top \phi(\mathbf{x}_j)$$
制約条件：
$$\sum_{i=1}^n \alpha_i y_i = 0, \quad 0 \leq \alpha_i \leq C \quad $$
式の意味を説明すると、
$\alpha_i$ (ラグランジュ乗数)
- $\alpha_i$ は各データ点に対応する重みを表します。
- $\alpha_i > 0$ のデータ点は、サポートベクター（マージン上または誤分類を許容するデータ点）になります。
- $\alpha_i = 0$ のデータ点は、分類に直接影響を与えません。
最適化関数の第1項：$\sum_{i=1}^n \alpha_i$
- 各データ点のラグランジュ乗数を最大化する項です。
- この項は、サポートベクターを増やし、データ点を分類するための情報を最大限に活用しようとします。
最適化関数の第2項：$- \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j \phi(\mathbf{x}_i)^\top \phi(\mathbf{x}_j)$
- この項は、データ点間の関係性を考慮して、ハイパープレーン（超平面）のマージンを最大化します。
- $\phi(\mathbf{x}_i)^\top \phi(\mathbf{x}_j)$ は、変換された「高次元空間での内積」です。
制約条件1：$\sum_{i=1}^n \alpha_i y_i = 0$
- データ点が正しい方向に分類されるようにするための制約条件です。
- $y_i$ はラベル（+1 または -1）で、$\alpha_i$ の合計がゼロになることで、クラス間のバランスを保ちます。
制約条件2：$\quad 0 \leq \alpha_i \leq C \quad $
- $\alpha_i$ の範囲を制限します。
- $C$ は、誤分類に対するペナルティを調整するハイパーパラメータで、大きいほど誤分類を許容しなくなります。
長くなりましたが、最適化関数の第二項における$ \phi(\mathbf{x}_i)^\top \phi(\mathbf{x}_j) $に注目すると$ x_i $, $ x_j $が非線形変換された関数の内積を計算していることがわかります。
この計算は元の空間が二次元程度であれば問題ないですが、さらに高次元になるほど計算コストが非常に大きくなります。
そこで登場するのが「カーネルトリック」です。
カーネルトリック
カーネルトリックとはカーネル関数を使うことで、高次元空間での計算を行わずに内積の結果を取得できる手法になります。
具体的には、
$$K(\mathbf{x}_i, \mathbf{x}_j) = \phi(\mathbf{x}_i)^\top \phi(\mathbf{x}_j)$$
と高次元空間の内積をカーネル関数でおきます。ここで、$K(\mathbf{x}_i, \mathbf{x}_j)$ は元の入力空間で計算されるため、高次元空間における内積を明示的に求める必要がなくなるのです。
よく使用されるカーネル関数は以下のとおりです。
◼️多項式カーネル
多項式カーネルは、元の空間での内積を多項式の形で変換します。次数 $d$ を指定することで、非線形な変換を行います。 $c$ と $d$ はハイパーパラメータです。
$$K(x_i, x_j) = (x_i \cdot x_j + c)^d$$
◼️RBFカーネル
RBFカーネル（ガウスカーネル）は、データ点間の距離を基にして計算されるカーネルで、非常に一般的です。無限次元の特徴空間にマッピングするため、非線形問題に適しています。 $\sigma$ はハイパーパラメータです。
$$K(x_i, x_j) = \exp\left(-\frac{|x_i – x_j|^2}{2\sigma^2}\right)$$
◼️シグモイドカーネル
シグモイドカーネルは、ニューラルネットワークの活性化関数としても知られるシグモイド関数をカーネルに適用したものです。$ c $と$ \alpha $はハイパーパラメータです。
$$K(x_i, x_j) = \tanh(\alpha x_i \cdot x_j + c)$$
これらのカーネル関数を使用することで、簡単に$ \phi(\mathbf{x}_i)^\top \phi(\mathbf{x}_j) $の結果を計算することができます。
注意事項として、適用するするデータによって最適なカーネル関数が異なり、カーネル関数ごとにハイパーパラメータが存在するので、交差検証などをうまく使って最適なカーネル関数を選択するようにしましょう。
以上、このカーネルトリックを使用して先ほどのラグランジュ乗数を用いた最適化関数を解くことでデータを分類する超平面を決定することができます。
終わりに
SVMについてわかりやすく解説したつもりですが、いかがでしょうか。一般的な線形問題については比較的理解しやすかったのではないしょうか？一方、発展として非線形問題も解説させていただきましたが、こちらは理解が少し難しいかと思います。私も理解するまで時間がかかりました。業務で少し使用したい程度であれば、なんとなくの意味や計算の流れが理解できればいいと感じてます。少しでも皆様の理解の一助となれれば幸いです。
