こんにちは!ぼりたそです!
今回はサポートベクター回帰(SVR)に関してわかりやすくまとめてみました。
この記事は以下の要点でまとめています。
- サポートベクター回帰(SVR)とは?
- サポートベクター回帰(SVR)のアルゴリズム
- Pythonにて実行
- 非線形問題への拡張
- 終わりに
また、別の記事で学習用のCSVファイルを入力するだけでSVRを実行するPythonコードを紹介していますので、興味のある方は参考にしていただければと思います。
それでは、以下順に解説していきます。
サポートベクター回帰(SVR)とは?
サポートベクター回帰(SVR)は、サポートベクターマシン(SVM)を応用した回帰手法であり、一般の回帰手法と同様にデータに対して最適な回帰モデルを構築し、新しいデータの値を予測することが目的です。
SVMについては過去にまとめた記事がありますので、興味のある方は参照いただければと思います。
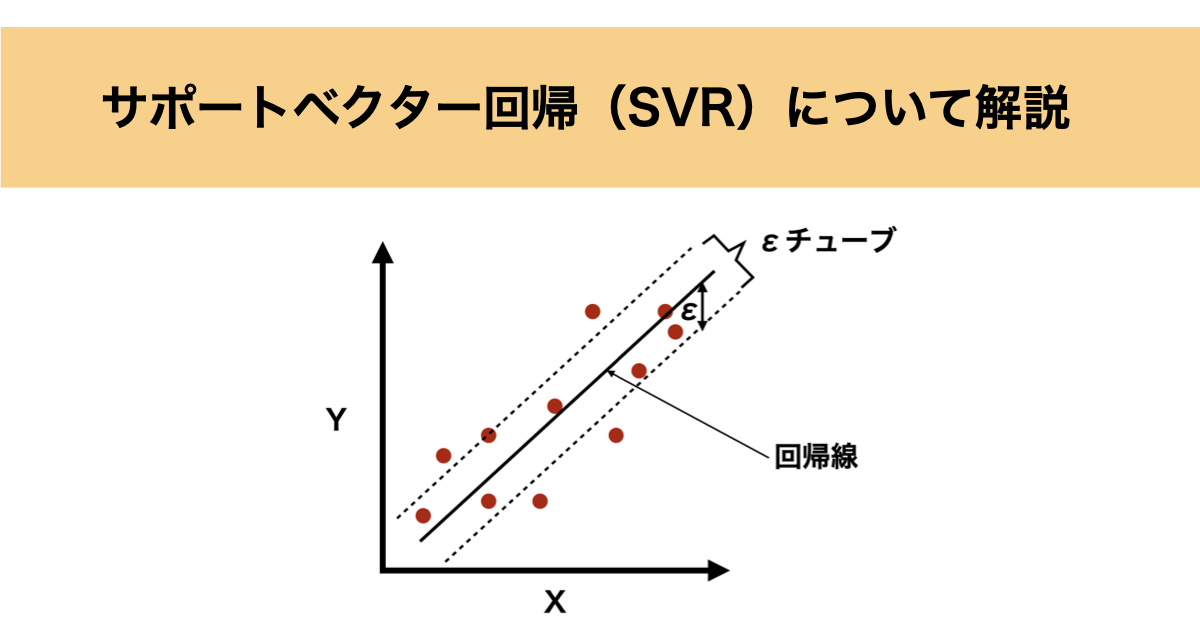
ただし、他の回帰モデルと異なるのは、「すべてのデータ点を正確に通る必要はない」という考え方です。
代わりに、一定の誤差範囲(εチューブ)内になるべくデータ点が収まるような回帰線を見つけます。これにより過学習を防ぎ、汎化性を向上することができます。
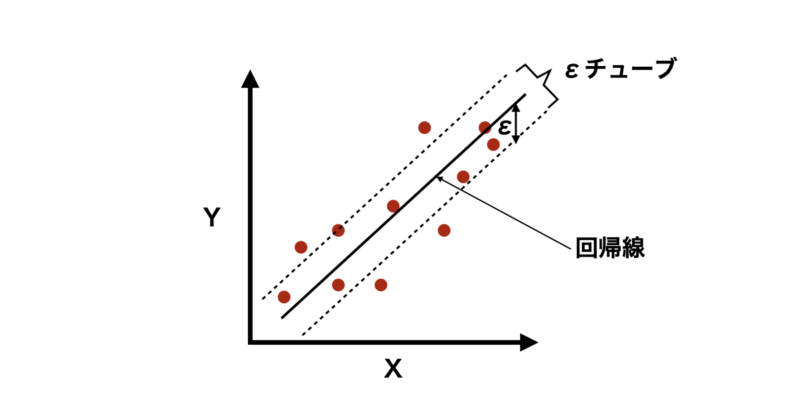

では、数式的な説明も含めて具体的なアルゴリズムについて紹介していきます。
サポートベクター回帰(SVR)のアルゴリズム
サポートベクター回帰のアルゴリズムとしては一定の誤差範囲(εチューブ)内にデータ点が収まるような回帰線を見つけることですが、具体的には以下の最小化問題を解くことにあたります。
$$\min_{w, b, \xi^{+}, \xi^{-}} \frac{1}{2} \require{physics}\norm{w}^2 + C \sum_{i=1}^n (\xi_i^{+} + \xi_i^{-})$$
ここで:
- $w$:各変数の重みベクトル
- $b$:バイアス項
- $\xi_i^{+}, \xi_i^{-}$:スラック変数(許容誤差を超える部分を表す)
- $C$:正則化パラメータ(変数の重みと許容誤差のトレードオフを制御)
数式の内容を説明すると、
まず、第一項:$\frac{1}{2} \require{physics}\norm{w}^2$ は正則化項になります。
具体的には、重みベクトル $w$ のノルム(長さ)の二乗を最小化することで、モデルが極端に複雑になるのを防ぎます。
この項により重み $w$ が極端に大きくなったり小さくなったりして、モデルが学習データに対して過学習を起こすリスクを軽減してくれます。
次に第二項:$C \sum_{i=1}^n (\xi_i^{+} + \xi_i^{-})$ はデータ点の誤差($\epsilon$-チューブを超えた部分)を表す項です。
$\xi_i^{+}$, $ \xi_i^{-}$はそれぞれ$\epsilon$-チューブの上側、下側からどれだけ外れているかを表している誤差の変数になります。
$\epsilon$-チューブ外の誤差を抑えることで、モデルがデータに対して適切にフィットするようにします。
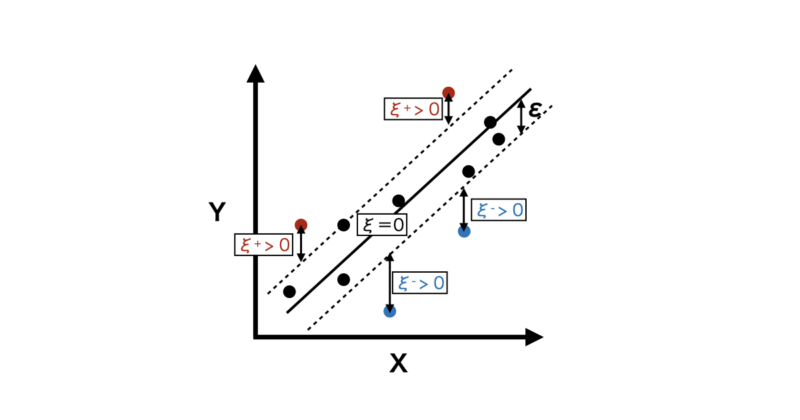

また、$C$ はハイパーパラメータであり、第一項(モデルの複雑さ)と第二項(誤差)とのバランスを調整します。
- $C$ が大きい場合:誤差を小さくすることを優先(高精度だが過学習のリスクが高い)。
- $C$ が小さい場合:モデルの複雑さを抑えることを優先(汎化性能が高いが精度が低下する可能性)。
以上の条件を満たしながら最適化関数を最小化することで以下のような回帰式を求めることができます。
$$\hat{y} = w^\top x + b$$
非線形問題への拡張
ここまでは、線形問題に対するSVRの説明でしたが、非線形問題に拡張した場合について説明していきます。
例えば、以下のように$ x $が変換関数$ \phi(\mathbf{x}) $により高次元へ変換されたとします。
$$\mathbf{x} \mapsto \phi(\mathbf{x})$$
この時、回帰式を決定するために以下のラグランジュ乗数を用いた以下の最適化関数を解く必要があります。
$$\min_{\alpha, \alpha^*} \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n (\alpha_i – \alpha_i^*)(\alpha_j – \alpha_j^*) K(\mathbf{x}_i, \mathbf{x}_j) + \epsilon \sum_{i=1}^n (\alpha_i + \alpha_i^*) – \sum_{i=1}^n y_i (\alpha_i – \alpha_i^*) $$
$$\text{制約条件: }
\begin{aligned}
& \sum_{i=1}^n (\alpha_i – \alpha_i^*) = 0, \ & 0 \leq \alpha_i, \alpha_i^* \leq C \quad \forall i.
\end{aligned}$$
この時、以下のようにカーネル関数 $K(\mathbf{x}_i, \mathbf{x}_j)$ を導入しており、これによって元の入力空間だけで内積が計算できるため、高次元空間における内積を明示的に求める必要がなくなるのです。
$$K(\mathbf{x}_i, \mathbf{x}_j) = \phi(\mathbf{x}_i)^\top \phi(\mathbf{x}_j)$$
よく使用されるカーネル関数は以下のとおりです。
◼️多項式カーネル
多項式カーネルは、元の空間での内積を多項式の形で変換します。次数 $d$ を指定することで、非線形な変換を行います。 $c$ と $d$ はハイパーパラメータです。
$$K(x_i, x_j) = (x_i \cdot x_j + c)^d$$
◼️RBFカーネル
RBFカーネル(ガウスカーネル)は、データ点間の距離を基にして計算されるカーネルで、非常に一般的です。無限次元の特徴空間にマッピングするため、非線形問題に適しています。 $\sigma$ はハイパーパラメータです。
$$K(x_i, x_j) = \exp\left(-\frac{|x_i – x_j|^2}{2\sigma^2}\right)$$
◼️シグモイドカーネル
シグモイドカーネルは、ニューラルネットワークの活性化関数としても知られるシグモイド関数をカーネルに適用したものです。$ c $と$ \alpha $はハイパーパラメータです。
$$K(x_i, x_j) = \tanh(\alpha x_i \cdot x_j + c)$$
少し脱線しましたが、最適化関数の数式の意味を説明すると、
まず第一項:$\frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n (\alpha_i – \alpha_i^*)(\alpha_j – \alpha_j^*) K(\mathbf{x}_i, \mathbf{x}_j) $
- この項は、SVRモデルの複雑さを表しています。線形SVRでは、正則化項である$\frac{1}{2} \require{physics}\norm{w}^2$(重みベクトルのノルムの二乗)に対応します。
- カーネル関数 $K(x_i, x_j)$ を用いて、入力データ $x_i$ と $x_j$ の間の非線形な関係を計算しています。これにより、適切な滑らかさを持つ回帰曲線を得ることができます。
- ラグランジュ乗数 $\alpha_i$ と $\alpha_i^*$ は、それぞれのデータ点がモデルにどの程度影響を与えるかを示します。
- この項を最小化することで、モデルの複雑さを抑え、過学習を防ぎます。
次に第二項:$\epsilon \sum_{i=1}^n (\alpha_i + \alpha_i^*)$
- イプシロン不感帯に関連するペナルティを加え、適切な柔軟性を確保する項になります。
- データがεチューブの外に位置する場合にペナルティを加えることで、学習モデルが柔軟性を持つように調整します。
- この項を最小化することで、モデルがターゲット値にフィットするようになりますが、εの値が小さいと、不感帯が狭くなり、モデルはデータに対して過学習となるリスクがあります。
次に第三項:$-\sum_{i=1}^n y_i (\alpha_i – \alpha_i^*) $
- この項は、モデルがターゲット値 $y_i$ にどれだけフィットしているかを示します。
- $(\alpha_i – \alpha_i^*)$ が小さいほど(この項を最大化するほど)、学習モデルにフィットすることになります。
- この項を最大化することで、モデルがターゲット値 $y_i$ によくフィットしますが、正則化パラメータ $C$ が大きい場合、この項が過剰に重視され、過学習のリスクが増加します。
重要なことは線形問題の時と同様に第一項と第二, 三項はトレードオフの関係になっているということです。
第一項を最小化しようとすると汎化性能は高いが精度が低下する可能性があり、第二, 三項を最小化しようとすると高精度だが過学習のリスクが高くなる可能性があります。
なので、二つの項を適切に最小化していく必要があるのです。
この最適化関数を解くことで以下のような回帰式を得ることができます。
$$\hat{y} = \sum_{i=1}^n (\alpha_i – \alpha_i^*) K(\mathbf{x}_i, \mathbf{x}_j) + b$$
Pythonでの実装
それでは、実際にSVRをPythonで実装してみましょう。
今回は以下の関数に従うデータを学習させて、きちんと予測できるかを検証していきます。
$$f(x) = \sin(x) \cdot \cos(x) \cdot x^{-1}$$
下に関数をプロットしたグラフを記載してますが、非線形な形状になっているのがわかります。
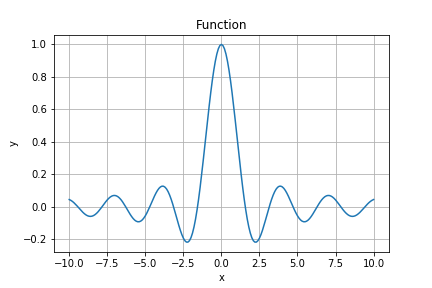

また、SVRを実行するにあたり、詳細な条件は以下の通りとなります。
| 条件 | 詳細 |
|---|---|
| 関数 | $f(x) = \sin(x) \cdot \cos(x) \cdot x^{-1}$ |
| データ数 | 100 (学習データ:テストデータ=8:2) |
| ハイパーパラメータ最適化 | グリッドサーチCV |
| CV(クロスバリデーション) | 10 fold CV |
以上の条件から作成したコードを以下に記載します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score
# 1. データ生成
np.random.seed(42)
x = np.linspace(1, 10, 100).reshape(-1, 1)
y = (np.sin(x) * np.cos(x) * x**-1).ravel() + np.random.normal(scale=0.05, size=100) # ノイズを追加
# 2. データの分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)
# 3. 標準化
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_test_scaled = scaler.transform(x_test)
# 4. ハイパーパラメータの最適化
param_grid = {
'C': [0.1, 1, 5, 10, 20],
'gamma': [0.01, 0.1, 1, 3, 5, 10]
}
svr = SVR(kernel='rbf')
grid_search = GridSearchCV(svr, param_grid, cv=10, scoring='r2')
grid_search.fit(x_train_scaled, y_train)
# 最適なモデルを取得
best_svr = grid_search.best_estimator_
# 5. モデルの学習と予測
train_r2 = best_svr.score(x_train_scaled, y_train)
y_pred = best_svr.predict(x_test_scaled)
# 6. 回帰式の導出(RBFカーネルの場合、明示的な式はなし)
print("Best Parameters:", grid_search.best_params_)
print(f"Training R^2: {train_r2:.3f}")
# 7. プロット
plt.figure(figsize=(10, 5))
# 実測値 vs 予測値
plt.scatter(y_test, y_pred, label='Predicted vs Actual', alpha=0.7)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', label='Ideal Line')
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('SVR Predictions vs Actual Values')
plt.legend()
plt.grid()
plt.show()
#Best Parameters: {'C': 5, 'gamma': 3}
#Training R^2: 0.825実際にコードを実行するとハイパーパラメータ最適化後のR2値が0.825ときちんと学習できていることがわかります。
また、学習後の予測値VS実測値のグラフも描画されます。これを見ると予測精度は問題なさそうですね。
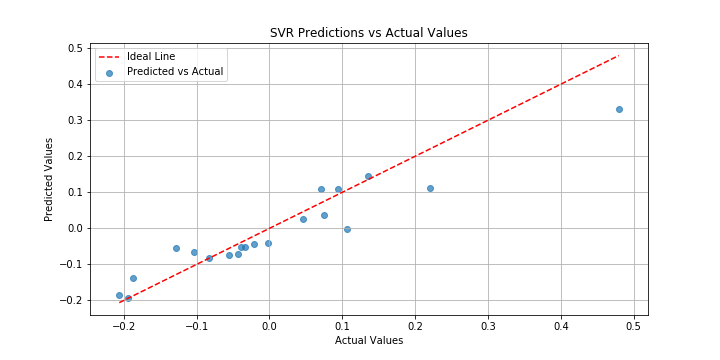

以上がPythonを使用したSVRの実行デモになります。
学習ステップをさらに進めたい方へ
SVRの基本的な概念を理解したら、
次はなぜマージンやε(イプシロン)がそのような役割を持つのか、
カーネルやハイパーパラメータが予測の振る舞いをどう変えるのかを、
仕組みとして整理しておきたいところです。
そのための理解を深めるのにおすすめなのが、
『図解即戦力 機械学習&ディープラーニングのしくみと技術がこれ一冊でしっかりわかる教科書』です。
本書は、コード実装を主目的とした解説書ではなく、
SVRを含む機械学習アルゴリズムの構造・考え方・学習の流れを、図解中心で解説する教科書です。
難解な数式に踏み込まず、回帰・分類・クラスタリングまでを通して、
「なぜそのモデル挙動になるのか」をブラックボックス化せずに理解できます。
たとえばSVRについても、
- C や ε がマージン幅や許容誤差にどう関与するのか
- RBFカーネルが「滑らかさ」や「局所性」をどう決めるのか
- 過学習・未学習がどのような条件で起こるのか
といった点を、数式やコードを追わなくても概念として整理できるため、
この先ハイパーパラメータ調整やモデル比較に進む際の判断軸が明確になります。
「SVRを使ってはいるが、なぜその設定でうまくいくのか説明できない」
「次は実装やチューニングに進みたいので、その前に仕組みを整理しておきたい」
そんな方にとって、実装フェーズへ進む前段階のインプットとして最適な一冊です。
本書で理解の土台を固めたうえで実装に取り組むことで、
“試す”から“意図して調整する”へと学習を一歩前に進められます。
一方で「Pythonはこれから…」「数式で挫折したことがある…」という方もいらっしゃるかと思います。
そんな初学者の方でもpythonで機械学習を実装できるようになるためのロードマップとオススメの教材について以下の記事にまとめていますので、興味のある方はご覧になって下さい。
終わりに
いかがだったでしょうか?SVRは過学習が起きにくく、汎化性の高い学習方法と言えます。また、線形、非線形問わずに使えるところも便利ですね。一方でアルゴリズムは少々理解しにくいところもあったと思います。ツールとしてSVRを使用する程度であれば、なんとなくアルゴリズムの流れが理解できていればいいと思っています。以上、長くなりましたが、SVRについて少しでも皆様の理解の一助になれば幸いです。