こんにちは!ぼりたそです!
今回はベイズ最適化の実行ライブラリであるOptunaを使用して目的変数が2つ以上である多目的最適化を実行する手法について記事を作成してみました。
Optunaを使用した単目的最適化については過去に記事を作成したのでご興味あれば以下の記事を参考いただければと思います。
今回の記事は以下のポイントでまとめています。
- Optunaについて
- 多目的最適化の設定
- 実行コード
- 実行コードの解説
- オススメの書籍
それでは順に解説していきます。
Optunaについて
まずはOptunaについて解説していきます。
Optunaはベイズ最適化(Bayesian Optimization)のためのPythonライブラリで、ハイパーパラメータの最適化などを容易に実装できるように設計されています。
Optunaの特徴としては主に以下の通りとなります。
■Optunaの特徴
以前、Optunaを使用した単目的最適化について記事でまとめていますが、今回は目的変数が二つ以上の同時最適化を行う多目的最適化の実行方法について解説したいと思います。
多目的最適化については以前記事でまとめていますので、参考にしていただければと思います。
多目的最適化の設定
次に今回実行する多目的最適化問題の設定についてご説明します。
今回は多目的最適化問題としてベンチマーク関数でもあるVMLOP2の最適化を実行したいと思います。
VMLOP2関数は以下2つの式で表せます。
$$f_1(x) = 1 – \exp \left( -\sum_{i=1}^{i} \left( \frac{{x_i – 1}}{{\sqrt{N}}} \right)^2 \right)$$
$$f_2(x) = 1 – \exp \left( -\sum_{i=1}^{i} \left( \frac{{x_i + 1}}{{\sqrt{N}}} \right)^2 \right)$$
$f_1(x)$と$f_2(x)$について、それぞれ入力したxに対して下限が0、上限が1になります。
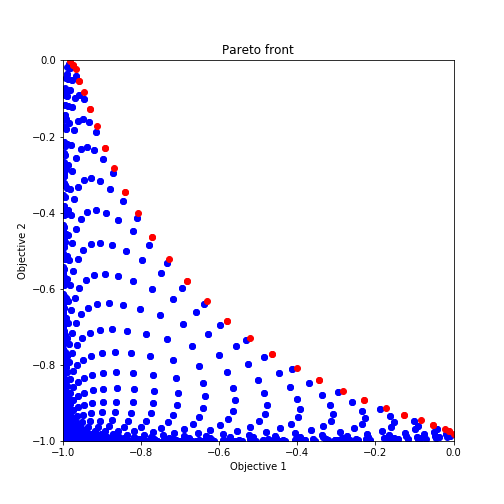
今回、入力するxを二次元として$f_1(x)$と$f_2(x)$の二次元グラフにプロットすると以下のようになります。互いの関数がトレードオフの関係になっているのがわかると思います。
赤丸でプロットした点はパレートフロントになっており、今回はこのパレートフロントからなるパレート超体積をどの程度まで広げられるかがお題になります。

また、具体的な探索条件などは以下のテーブルにまとめています。
Optunaではベイズ最適化のアルゴリズムとしてガウス過程回帰ではなくTPE(Tree-Structured Parzen Estimator)を採用しています。TPEについては後ほど別の記事でまとめられたらと思っています。
| 目標値 | VMLOP2のパレート超体積(0.345) |
| 学習データ(初期データ) | 無し |
| 最適化アルゴリズム | MOTPE(Multi-Objective Tree-structured Parzen Estimator) |
| 探索回数 | 200回 |
実行コード
それでは、実際にVMLOP2の関数について多目的最適化を実行してみましょう。
実行したコードは以下の通りとなります。
今回は探索状況をgifアニメーションで保存するために少々コードが冗長になってしまいました。
import optuna
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from optuna.pruners import SuccessiveHalvingPruner
# 目的関数を定義する関数
def VLMOP2(x):
n = len(x)
f1 = -(1 - np.exp(-1 * np.sum((x - 1/np.sqrt(n)) ** 2)))
f2 = -(1 - np.exp(-1 * np.sum((x + 1/np.sqrt(n)) ** 2)))
return f1, f2
#探索点を評価する関数
def objective(trial):
n = 2 # 関数の次元数
x = [trial.suggest_float(f'x{i}', -5, 5, step=0.01) for i in range(n)] # 探索範囲を-5から5まで1000刻みに設定
return VLMOP2(x)
#VLMOP2のPareto frontの計算
x = np.linspace(-5, 5, 100)
X1, X2 = np.meshgrid(x, x)
points = np.column_stack((X1.ravel(), X2.ravel()))
y = np.array([VLMOP2(point) for point in points])
pareto_front_vlmop2 = []
for point in y:
is_pareto = True
for other_point in y:
if (other_point[0] >= point[0] and other_point[1] >= point[1] and
(other_point[0] > point[0] or other_point[1] > point[1])):
is_pareto = False
break
if is_pareto:
pareto_front_vlmop2.append(point)
pareto_front_vlmop2 = np.array(pareto_front_vlmop2)
# 多目的最適化及び探索進捗を可視化する関数
def optimize_and_plot(num_trials, num_frames):
study = optuna.create_study(directions=['maximize', 'maximize'], sampler=optuna.samplers.MOTPESampler(),
pruner=SuccessiveHalvingPruner())
animation_data = []
def update(frame):
global pareto_front
study.optimize(objective, n_trials=1) # フレームごとのトライアル数を1に変更
trials = study.trials_dataframe()
f1, f2 = trials['values_0'], trials['values_1']
ax.clear()
ax.scatter(f1, f2, label='Optimized points') # 凡例を追加
ax.set_xlabel('f1')
ax.set_ylabel('f2')
ax.set_title(f'Optimization Progress (Frame {frame+1}/{num_frames})')
# Pareto frontの解を赤色でハイライト表示
pareto_front = np.array([t.values for t in study.best_trials]) # 最良トライアルからPareto frontを取得
ax.scatter(pareto_front[:, 0], pareto_front[:, 1], color='red', marker='o', label='Pareto front')
# VLMOP2のPareto frontを黒色でプロット
ax.plot(pareto_front_vlmop2[:, 0], pareto_front_vlmop2[:, 1], color='black', linewidth=2, label='VLMOP2 Pareto front')
ax.legend() # 凡例を表示
fig, ax = plt.subplots()
ani = FuncAnimation(fig, update, frames=num_frames, repeat=False)
ani.save('multi_objective_optimization.gif', writer='pillow', fps=7)
#パレート超体積を計算する関数
def pareto_hypervolume(pareto_front):
# 探索点のパレートフロントのf1を昇順に並び替え
pareto_front = pareto_front[np.argsort(pareto_front[:, 0])]
# パレート超体積の初期化
hypervolume = 0.0
# パレート超体積の計算
for i in range(len(pareto_front) - 1):
width = pareto_front[i + 1, 0] - pareto_front[i, 0]
height = pareto_front[i, 1]
hypervolume += width * (height+1)
return hypervolume
#多目的最適化を実行
optimize_and_plot(num_trials=200, num_frames=200)
# パレート超体積の計算を実行
hypervolume = pareto_hypervolume(pareto_front)
vlmop2_hypervolume = pareto_hypervolume(pareto_front_vlmop2)
print(f'VLMOP2のパレートフロント : {vlmop2_hypervolume}')
print(f'探索点のパレートフロント : {hypervolume}')
'''
VLMOP2のパレートフロント : 0.34549703030586165
探索点のパレートフロント : 0.31021040536297584
'''実行した結果は以下の通りとなります。
黒い線グラフがVLMOP2のパレートフロントになっており、赤いプロットが探索点におけるパレートフロント、青いプロットが探索点における劣解となります。
200回も探索するとほとんどパレート解周辺は探索できているようですね。
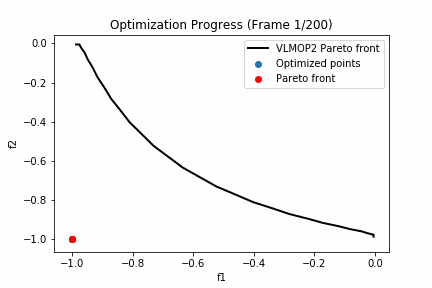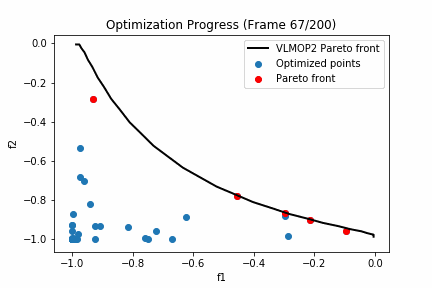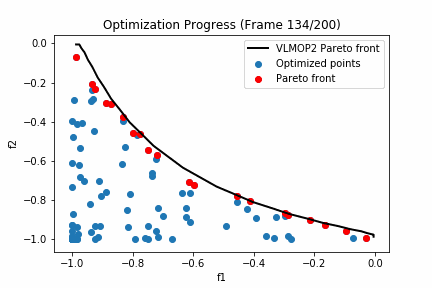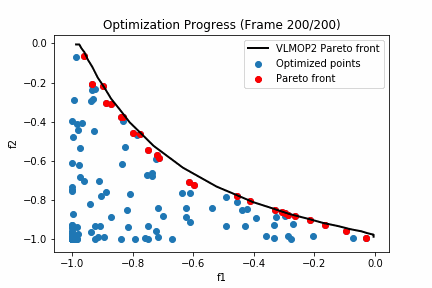

次にパレート超体積に注目してみましょう。VLMOP2のパレート超体積が0.345なのに対して今回探索したパレートフロントは0.310でした。つまり理論値に対して約90%探索できたということになりますね。
実行コードの解説
次に実行コードの解説に移りたいと思います。
探索の進捗を可視化するために少々冗長なコードとなっていますが、構成としてはざっくり以下の通りです。
- VLMOP2関数を定義する関数
- 目的関数を評価する関数
- 目的関数のパレートフロントの計算
- 多目的最適化を実行 (および探索進捗を可視化)する関数
- 探索点のパレート超体積を計算する関数
- 多目的最適化、パレート超体積の計算の実行
VLMOP2(目的関数)を定義する関数
まずは目的関数を定義する関数について説明していきます。
実行部分は以下の部分になります。
def VLMOP2(x):
n = len(x)
f1 = -(1 - np.exp(-1 * np.sum((x - 1/np.sqrt(n)) ** 2)))
f2 = -(1 - np.exp(-1 * np.sum((x + 1/np.sqrt(n)) ** 2)))
return f1, f2特別説明することはありませんが、後に登場するtrialによって探索された候補点xに対してVLMOP2関数の数式に従って$f_1(x)$と$f_2(x)$が返される関数となっています。
目的関数を評価する関数
次に目的関数を評価する関数についての説明になります。
ここでは探索するtrialを定義し、その後、探索した点を評価する関数となっています。
実行部分は以下の部分になります。
#探索点を評価する関数
def objective(trial):
n = 2 # 関数の次元数
x = [trial.suggest_float(f'x{i}', -5, 5, step=0.01) for i in range(n)] # 探索範囲を-5から5まで1000刻みに設定
return VLMOP2(x)今回は入力するxは二次元としており、「n = 2」の部分で設定しています。
「x = [trial.suggest_float(f’x{i}’, -5, 5, step=0.01) for i in range(n)] 」の部分で探索を実行するtrialを定義しており、今回は-5から5の範囲から探索するように設定しております。
目的関数のパレートフロントの計算
次に目的関数のパレートフロントの計算です。
ここでは単純に目的関数であるVLMOP2のパレートフロントを泥臭く計算しているというコードになっています。
実行部分は以下の部分になります。
#VLMOP2のPareto frontの計算
x = np.linspace(-5, 5, 100)
X1, X2 = np.meshgrid(x, x)
points = np.column_stack((X1.ravel(), X2.ravel()))
y = np.array([VLMOP2(point) for point in points])
pareto_front_vlmop2 = []
for point in y:
is_pareto = True
for other_point in y:
if (other_point[0] >= point[0] and other_point[1] >= point[1] and
(other_point[0] > point[0] or other_point[1] > point[1])):
is_pareto = False
break
if is_pareto:
pareto_front_vlmop2.append(point)
pareto_front_vlmop2 = np.array(pareto_front_vlmop2)2-4行目で-5から5の範囲で二次元グリッドの点を生成し、5行目で先ほど作成したVLMOP2の関数を使用してグリッド点について全て計算しています。
その後、6-16行目で計算した生成点について劣解を省いて、パレート解のみを「pareto_front_vlmop2」に格納しています。
最後に「pareto_front_vlmop2」をnumpy行列に変換しているというコードになります。
多目的最適化を実行 (および探索進捗を可視化)する関数
次に多目的最適化を実行および探索進捗を可視化する関数についての説明です。
この関数は多目的最適化を実行し、その探索進捗を二次元グラフのgifアニメーションとして可視化するコードになります。
この部分がかなり複雑になってしまいました…
実行部分は以下の部分になります。
# 多目的最適化及び探索進捗を可視化する関数
def optimize_and_plot(num_trials, num_frames):
study = optuna.create_study(directions=['maximize', 'maximize'], sampler=optuna.samplers.MOTPESampler(),
pruner=SuccessiveHalvingPruner())
animation_data = []
def update(frame):
global pareto_front
study.optimize(objective, n_trials=1) # フレームごとのトライアル数を1に変更
trials = study.trials_dataframe()
f1, f2 = trials['values_0'], trials['values_1']
ax.clear()
ax.scatter(f1, f2, label='Optimized points') # 凡例を追加
ax.set_xlabel('f1')
ax.set_ylabel('f2')
ax.set_title(f'Optimization Progress (Frame {frame+1}/{num_frames})')
# Pareto frontの解を赤色でハイライト表示
pareto_front = np.array([t.values for t in study.best_trials]) # 最良トライアルからPareto frontを取得
ax.scatter(pareto_front[:, 0], pareto_front[:, 1], color='red', marker='o', label='Pareto front')
# VLMOP2のPareto frontを黒色でプロット
ax.plot(pareto_front_vlmop2[:, 0], pareto_front_vlmop2[:, 1], color='black', linewidth=2, label='VLMOP2 Pareto front')
ax.legend() # 凡例を表示
fig, ax = plt.subplots()
ani = FuncAnimation(fig, update, frames=num_frames, repeat=False)
ani.save('multi_objective_optimization.gif', writer='pillow', fps=7)
このコードはまずoptimize_and_plot関数として定義しており、引数としてnum_trialsは探索回数、num_framesは探索進捗を可視化するgifアニメーションのフレーム数を設定します。
細かく中身を見ると、3行目でstudyオブジェクトを生成しています。このstudyオブジェクトでは探索の方針を設定しています。
引数としてdirectionで最大化 or 最小化を設定しており、今回、$f_1(x)$と$f_2(x)$のどちらも最大化するように設定しています。
また、samplerでは探索アルゴリズムを指定しており今回はMPTPE(Multi-Objective Tree-structured Parzen Estimator)を使用しています。TPEの多目的拡張バージョンみたいなものです。
その後、7行目のupdate関数を設定しており、この関数で実際に最適化を実行して同時に探索進捗を可視化する関数になります。
「study.optimize(objective, n_trials=1)」の部分で先ほど作成したstudyオブジェクトを使用して多目的最適化を実行します。引数としてobjective関数(trialを定義した関数)とn_trialsとして一度の探索数を設定しています。
残りの説明は最適化とは関係ないので詳細な説明は省略させていただきますが、探索点と探索点のパレート解、VLOMP2のパレート解を一つのグラフに表示してgifアニメーションの1フレームとして保存するように設定されています。
探索点のパレート超体積を計算する関数
探索点のパレート超体積を計算する関数について説明します。
ここでは文字通り、探索した候補点におけるパレート超体積を計算する関数になっています。
実行部分は以下の部分になります。
#パレート超体積を計算する関数
def pareto_hypervolume(pareto_front):
# 探索点のパレートフロントのf1を昇順に並び替え
pareto_front = pareto_front[np.argsort(pareto_front[:, 0])]
# パレート超体積の初期化
hypervolume = 0.0
# パレート超体積の計算
for i in range(len(pareto_front) - 1):
width = pareto_front[i + 1, 0] - pareto_front[i, 0]
height = pareto_front[i, 1]
hypervolume += width * (height+1)
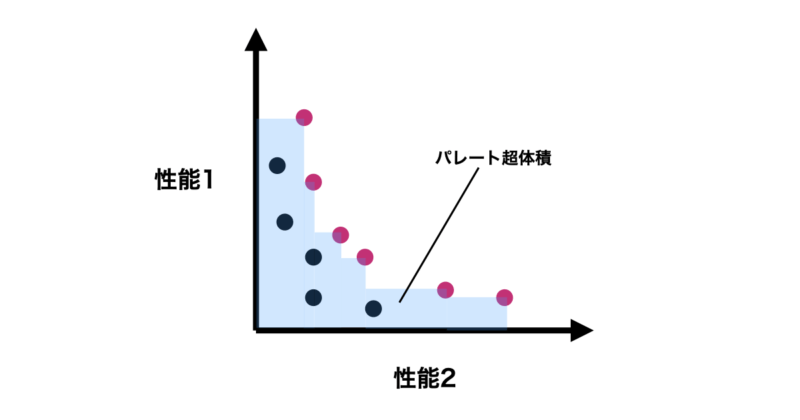
return hypervolume こちらは探索した候補点のパレート解を引数とすることでパレート超体積を計算できるようになっており、アナログ式にパレートフロント間で幅と高さから二次元面積を計算して足し合わせることで計算しています。
イメージとしては下の図の青い部分の面積を計算しているような手法になります。

多目的最適化、パレートフロントの計算の実行
最後に多目的最適化、パレートフロントの計算の実行についての説明です。
この部分は説明することはあまりありませんが、設定した関数を使用して実際に計算を実行する部分になります。
実行部分は以下の部分になります。
#多目的最適化を実行
optimize_and_plot(num_trials=200, num_frames=200)
# パレート超体積の計算を実行
hypervolume = pareto_hypervolume(pareto_front)
vlmop2_hypervolume = pareto_hypervolume(pareto_front_vlmop2)
print(f'VLMOP2のパレートフロント : {vlmop2_hypervolume}')
print(f'探索点のパレートフロント : {hypervolume}')2行目でoptimize_and_plot関数を使用して多目的最適化を実行しており、探索回数を200回、gifアニメーションのフレーム数も合わせて200で設定しています。
次にpareto_hypervolume関数で探索点と解であるVLMOP2のパレート超体積を計算して出力するように設定しています。
オススメの書籍
最後にオススメの書籍についてご紹介します。
Optunaを使用したベイズ最適化についてもっと勉強したいという方には以下に紹介する「ベイズ最適化 適応的実験計画の基礎と実践」という書籍がオススメです。
この書籍にはベイズ最適化の理論はもちろんのことPythonライブラリであるOptunaの仕組みや単目的、多目的最適化の実装方法についても記載されています。
書籍の難易度としては完全に初学者向けというわけではないですが、ベイズ最適化について概要をある程度知っている人なら読めるかと思います。
ベイズ最適化についてもっと勉強したい方、Optunaを使用して単目的、多目的最適化を実行したい方はぜひ購入いただければと思います。
ベイズ最適化のオススメ参考書については以下の記事でもまとめていますので、興味のある方はご参照いただければと思います。
終わりに
いかがでしたでしょうか?今回の実行コードは色々とごちゃついていましたが、基本的にはOptunaは「trial」, 「study」, 「sampler」の三つがきちんと設定されていれば最適化は動かすことができるはずです。実際に実験候補の探索を行うコードを書ければよかったのですが、それはまた別の機会に!