Optunaでベイズ最適化を実行

Python
2024.02.23

こんにちは！ぼりたそです！

今回はベイズ最適化ライブラリであるOptunaを使用してベイズ最適化を実行する手法について解説していきます

この記事は以下のポイントでまとめています。

Point
  • Optunaとは
    　
  • ベイズ最適化のフロー
    　
  • ベイズ最適化の実行コード
    　
  • 実行コードの解説
    　
  • オススメの書籍

同様にベイズ最適化を実行するライブラリであるGPyOptを使用したコードや、Optunaを使用した多目的最適化について以前にまとめていますので、興味のある方は参考にしていただければと思います。

合わせて読みたい
Optunaで多目的最適化を実行
この記事はOptunaで多目的最適化を実行する手法について解説しています。具体的には「Optunaについて」、「多目的最適化の実行フロー」、「実行コードとその解説」のトピックについて説明しています。
boritaso-blog.com
2024.03.24
合わせて読みたい
【コード付き】GpyOptでベイズ最適化を実行
この記事はGPyOptでベイズ最適化を実行する手法について解説しています。具体的にはGPyOptとは？実装コードとその解説について詳細に説明している記事となります。
boritaso-blog.com
2023.10.22
合わせて読みたい
GPyOptで化合物探索プログラムを実装
この記事ではGpyOptを使った化合物の探索プログラムを実装する方法について解説した記事になります。具体的にはGPyOptとは、探索の流れ、使用コード説明、探索結果について記載しています。
boritaso-blog.com
2024.01.24

それでは順番に解説していきます。

スポンサーリンク

Optunaとは

まずはOptunaについてご紹介していきます。

Optunaはベイズ最適化（Bayesian Optimization）のためのPythonライブラリで、ハイパーパラメータの最適化などを容易に実装できるように設計されています。

ベイズ最適化とは機械学習の手法の一つであり、現状のデータから効率的に目標値を達成できる最適化手法となっています。

詳しくは以下の記事にまとめてありますので、ご参考いただければと思います。

合わせて読みたい
【初心者向け】ベイズ最適化についてわかりやすく説明
この記事はベイズ最適化について初心者向けにまとめた記事です。ベイズ最適化についてメリット, デメリットや実行プロセスについてまとめています。
boritaso-blog.com
2023.07.26

Optunaの主な特徴は以下の通りです。

■Optunaの特徴

  • 柔軟な探索空間の定義:
    Optunaでは、連続的なパラメータ、離散的なパラメータ、整数型のパラメータなど、さまざまなタイプの探索空間を定義することができます。
    　
  • 並列化のサポート:
    Optunaは並列化をサポートしており、複数のトライアルを同時に実行することができます。これにより、計算リソースの効率的な利用が可能です。
    　
  • 可視化機能:
    Optunaは、探索プロセスや結果の可視化を行うための機能を多く提供しており、探索の進行状況や最適なパラメータの値を視覚的に理解するのに適しています。
    　

ベイズ最適化の実行フロー

次に今回実装するベイズ最適化のフローについてご説明します。

本記事では以下の関数について最大点を見つけるために最適化を実行していきます。

$$f(x) = \sin(x) \cdot \cos(x) \cdot x^{-1}$$

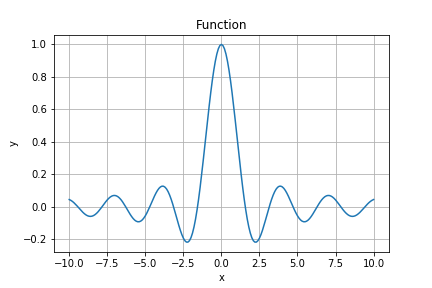
最大値となるのがx=0の時ですが、果たして最適化で導き出せるのでしょうか？というのが今回のお題ですね。

具体的な条件については以下の通りとなります。

Optunaではベイズ最適化のアルゴリズムとしてガウス過程回帰ではなくTPE(Tree-Structured Parzen Estimator)を採用しています。TPEについては後ほど別の記事でまとめられたらと思っています。

目標値$f(x) = \sin(x) \cdot \cos(x) \cdot x^{-1}$の最大化
学習データ（初期データ）無し
探索モデルTPE(Tree-Structured Parzen Estimator)
探索回数30回

ベイズ最適化の実行コード

それでは実際にOptunaを使用してベイズ最適化を実行していきましょう。

実行コードは以下の通りです。

import optuna
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# Objective function
def objective(x):
    return np.cos(x) * x**-1 * np.sin(x)

# Define the search space
def objective_optuna(trial):
    x = trial.suggest_float("x", -10, 10)
    return objective(x)

# Visualization function
def plot_optimization_process(i, ax, study):
    ax.clear()
    x = np.linspace(-10, 10, 100)
    y = objective(x)
    ax.plot(x, y, label='Objective Function')
    for t in study.trials[:i]:
        if t.state == optuna.trial.TrialState.COMPLETE:
            x_trial = t.params['x']
            y_trial = objective(x_trial)
            ax.scatter(x_trial, y_trial, color='red', zorder=5)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.legend()
    ax.set_title(f"Iteration {i+1}")

# Define the optimization study
study = optuna.create_study(direction="maximize", sampler=optuna.samplers.TPESampler(), pruner=optuna.pruners.MedianPruner())
study.optimize(objective_optuna, n_trials=30)

# Create gif animation
fig, ax = plt.subplots()
ani = FuncAnimation(fig, plot_optimization_process, frames=len(study.trials), fargs=(ax, study))
ani.save('optimization_process.gif', writer='pillow')
plt.show()

# Get the best parameter
best_params = study.best_params
best_value = study.best_value

print("Best value:", best_value)
print("Best parameters:", best_params)

#Best value: 0.9998662139815366
#Best parameters: {'x': -0.014166406834550394}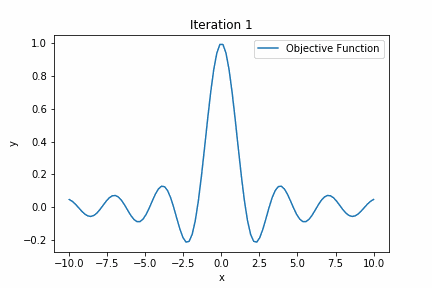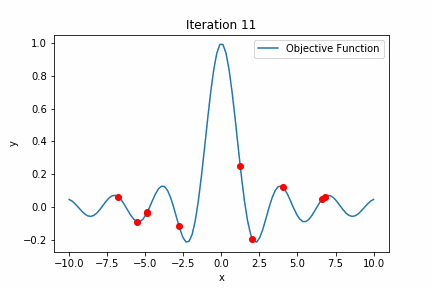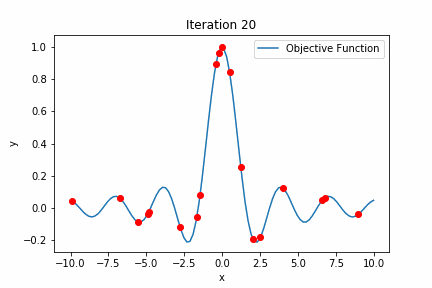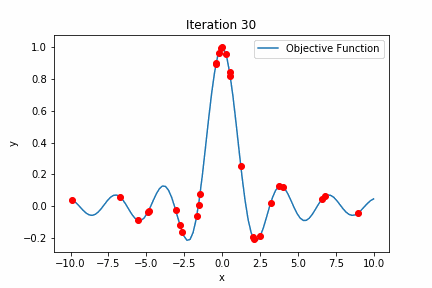

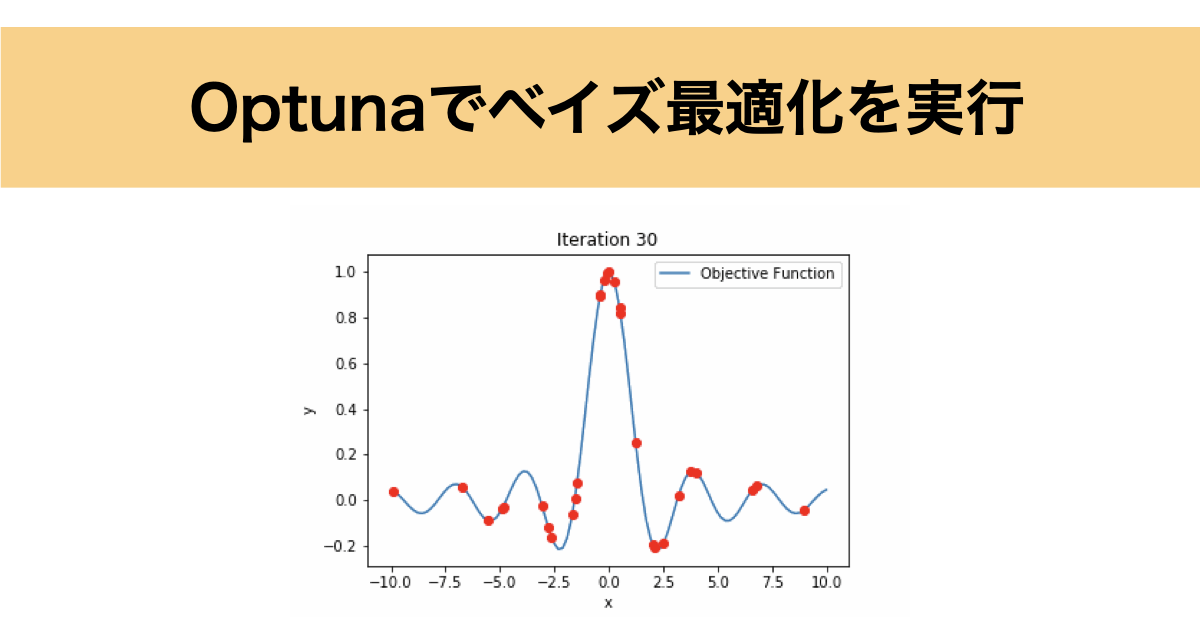
出力結果を見てみると

Best value: 0.9998662139815366
Best parameters: {‘x’: -0.014166406834550394}

と出力されており、ほぼ最高値を探索できていますね。

ちなみに探索数は30回に設定していますが、最高値を探索できたのは12回目になっています。

ではここからコードの解説をしていきたいと思います。

スポンサーリンク

実行コードの解説

では次に実行コードの解説をしていきたいと思います。

今回の実行コードは以下のプロセスで動いています。

  • 各ライブラリのインポート
    　
  • 目的関数の定義
    　
  • 探索範囲の定義
    　
  • 可視化関数の定義
    　
  • 最適化オブジェクトの定義&実行
    　
  • 可視化グラフの生成
    　
  • 最良パラメータの出力

それでは順に解説していきます。

各ライブラリのインポート

まずは各ライブラリのインポートについてです。

ライブラリのインポートは以下の部分で実行しています。

import optuna
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

Optunaのインストールが完了していない場合は以下のコードを実行してインストールしましょう。

!pip install optuna

目的関数の定義

次に目的関数の定義についてです。

今回のコードでは以下の部分で定義しています。

# Objective function
def objective(x):
    return np.cos(x) * x**-1 * np.sin(x)

単純に引数のxから関数の値が返ってくるように定義されています。

探索範囲の定義

次は探索範囲の定義についてです。

今回は以下の部分で定義しています。

# Define the search space
def objective_optuna(trial):
    x = trial.suggest_float("x", -10, 10)
    return objective(x)

この関数自体はtrial.suggest_floatメソッドで次の候補をxに代入して、先ほどの目的関数の値を返すコードになっています。

このtrial.suggest_floatの引数として設定されているのが探索範囲であり、今回は-10から10を探索範囲としています。

引数の種類としてはいくつかあり、下のテーブルに示します。

　引数名　　型　説明
namestr説明変数の名前を設定。必須項目
lowfloat説明変数の探索範囲の下限を設定。必須項目
highfloat説明変数の探索範囲の上限を設定。必須項目
stepfloat,str離散化ステップを指定する。デフォルトはNone
logbool対数ドメインからサンプリングするか指定。デフォルトはFalse　

可視化関数の定義

次は可視化関数の定義についてです。

今回は以下の部分で実行しています。

# Visualization function
def plot_optimization_process(i, ax, study):
    ax.clear()
    x = np.linspace(-10, 10, 100)
    y = objective(x)
    ax.plot(x, y, label='Objective Function')
    for t in study.trials[:i]:
        if t.state == optuna.trial.TrialState.COMPLETE:
            x_trial = t.params['x']
            y_trial = objective(x_trial)
            ax.scatter(x_trial, y_trial, color='red', zorder=5)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.legend()
    ax.set_title(f"Iteration {i+1}")

コードとしては1〜4行目ではグラフを初期化して目的関数のx, yを設定してをプロットしています。

5〜9行目で探索したx,yの組を順に目的関数のグラフ上にプロットしています。

10〜13行目ではラベルや凡例を記載するように設定しています。

最適化オブジェクトの定義＆実行

次に最適化オブジェクトの定義＆実行について説明します。

今回のコードでは以下の部分で実行しています。

# Define the optimization study
study = optuna.create_study(direction="maximize", sampler=optuna.samplers.TPESampler(), pruner=optuna.pruners.MedianPruner())
study.optimize(objective_optuna, n_trials=30)

optuna.create_studyの部分で最適化の設定をしており、directionでは関数の最適化方向を決めています。今回は最大化したいのでmaximizeに設定しています。

samplerでは探索空間上の候補を生成するモデルを指定しています。今回はTPEを指定しています。

prunerでは目的達成が見込まれない不要な試行を早期に中止する設定を行なっています。今回はMedianPrunerを使用しています。これは各試行の目的関数の値の中央値を計算し、その中央値よりも悪い試行を早期に中止します。これにより、探索空間の一部で性能が悪い試行を即座に除外し、リソースを効果的に使用することができます。

可視化グラフの生成

次に可視化グラフの生成についてです。

今回のコードでは以下の部分で実行しています。

# Create gif animation
fig, ax = plt.subplots()
ani = FuncAnimation(fig, plot_optimization_process, frames=len(study.trials), fargs=(ax, study))
ani.save('optimization_process.gif', writer='pillow')
plt.show()

GIFアニメーションを生成するコードになっており、FunAnimationにて色々と設定してます。figは描画するグラフのオブジェクトになってます。

plot_optimization_processは先ほど定義した可視化グラフの関数で各フレームごとに呼び出されます。

framesはGIFを何フレームにするかの設定です。これは今回の探索回数である30回に設定しています。

最良パラメータの出力

最後に最良パラメータの出力です。

今回は以下の部分で実行しています。

# Get the best parameter
best_params = study.best_params
best_value = study.best_value

print("Best value:", best_value)
print("Best parameters:", best_params)

best_params, best_valueにてそれぞれ最良のxとその値であるyを代入し、print関数にて出力しています。

以上が今回のコードの解説になります。

オススメの書籍

最後にオススメの書籍についてご紹介します。

Optunaを使用したベイズ最適化についてもっと勉強したいという方には以下に紹介する「ベイズ最適化　適応的実験計画の基礎と実践」という書籍がオススメです。

この書籍にはベイズ最適化の理論はもちろんのことPythonライブラリであるOptunaの仕組みや単目的、多目的最適化の実装方法についても記載されています。

書籍の難易度としては完全に初学者向けというわけではないですが、ベイズ最適化について概要をある程度知っている人なら読めるかと思います。

ベイズ最適化についてもっと勉強したい方、Optunaを使用して単目的、多目的最適化を実行したい方はぜひ購入いただければと思います。

ベイズ最適化: 適応的実験計画の基礎と実践
¥4,180 （2024/04/26 06:45時点 | Amazon調べ）
Amazon
楽天市場

ベイズ最適化のオススメ参考書については以下の記事でもまとめていますので、興味のある方はご参照いただければと思います。

合わせて読みたい
ベイズ最適化のオススメ参考書2冊
本記事はベイズ最適化のオススメ参考書2冊についてまとめた記事になります。具体的には「Pythonで学ぶ実験計画法入門 ベイズ最適化によるデータ解析」、「ベイズ最適化 適応的実験計画の基礎と実践」の2冊について紹介しています。
boritaso-blog.com
2024.09.29

終わりに

以上がOptunaにてベイズ最適化を実行する手法に関する説明になります。今回は可視化関数などを使用していましたが、最良パラメータを探索するくらいなら結構簡単に実装できます。また、探索モデルはGP（ガウス過程回帰）ではなく、TPEをデフォルトで使用しており面白いですね。今回は最初から答えがわかっている目的関数を設定しましたが、次は答えがわからないブラックスボックス関数の評価もしてみたいですね。

スポンサーリンク
タイトルとURLをコピーしました