こんにちは!ぼりたそです!今回はベイズ最適化について初学者の方に向けてわかりやすく説明した記事を作成してみました。
この記事は以下のポイントでまとめています。
- ベイズ最適化とは?
- ベイズ最適化のメリット、デメリット
- ベイス最適化のプロセス
- オススメの書籍
それでは詳細に説明していきます。
ベイズ最適化とは?
ベイズ最適化は、少ない試行回数で効率よく最適な条件を見つけるための機械学習の手法です。
最近では、材料開発(マテリアルズ・インフォマティクス:MI)、機械学習のハイパーパラメータ調整、新薬の探索、工場の生産条件の最適化など、さまざまな分野で使われています。
例えば、あなたが料理人で「最高に美味しいスープ」を作りたいとき、
塩、コショウ、酒、みりんの比率をどう調整すればよいかをできるだけ少ない試作で見つけ出すイメージです。
このとき役立つのがベイズ最適化です。
ベイズ最適化のメリット、デメリット
次にベイズ最適化のメリット、デメリットについて解説します。
まずはメリットについて以下にまとめます。
メリット
次にデメリットについて以下にまとめます。
デメリット
以上がベイズ最適化のメリットとデメリットになります。メリットに目がいってしまいますが、デメリットも許容した上で使用する必要がありますね。
特に局所解への収束はよくあることなので、気をつける必要があります!
ベイズ最適化のプロセス
最後にベイズ最適化のプロセスについてご説明します。
ベイズ最適化のフローとしては下に示すように大きく5つになります。
- 事前実験
- サンプルの評価
- ベイズ的な更新
- 次のサンプル選択
- 反復
ここでは先ほどと同様に料理のレシピに例えてご説明していきます。
あなたは料理人であり美味しいスープを作りたいとします。
調味料は塩、コショウ、酒、みりんの四種類です。この調味料を組み合わせて美味しいスープを作るためにベイズ最適化を用いてレシピを考えることにしました。

それではベイズ最適化のプロセスについて順番にご説明していきます。
1. 事前実験
最初に、料理の材料の範囲を考え、可能性のあるレシピをいくつか考えます。これは経験や推測のもと当たりをつけたもので構いません。そのレシピに従ってそれぞれスープを作ります。
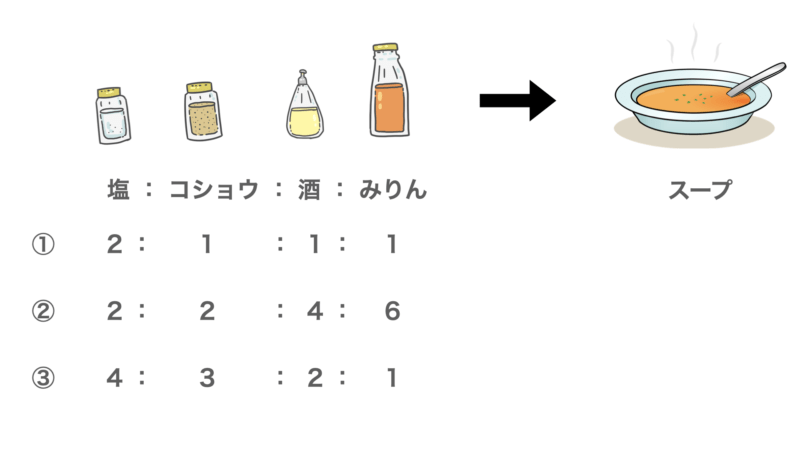
2. サンプルの評価
次に考案したレシピに従って作ったスープの試食を行います。そして、レシピに対する美味しさの評価を記録します。
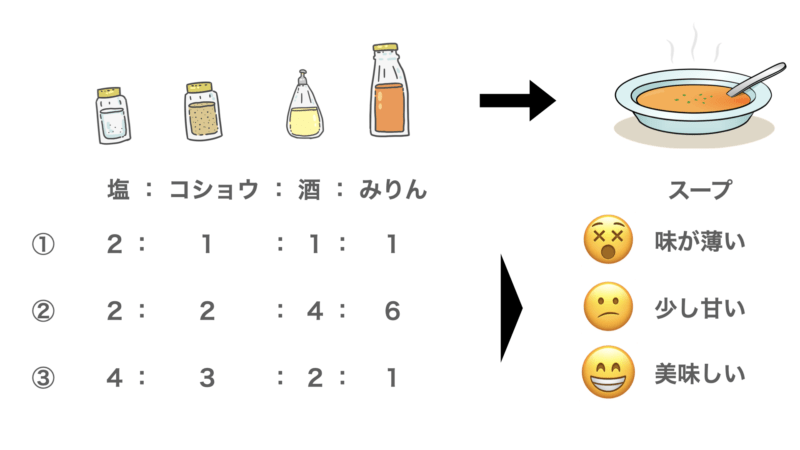
3. 予測モデルの更新
試食結果を元に、レシピの「おいしさ予想」と「不確実性(味のブレ)」を計算します。具体的には下図の事後分布のように美味しさの予測線(青線)と不確実性(青帯)を計算します。
この事後分布によって、まだ試していないレシピの美味しさを推測することができます。
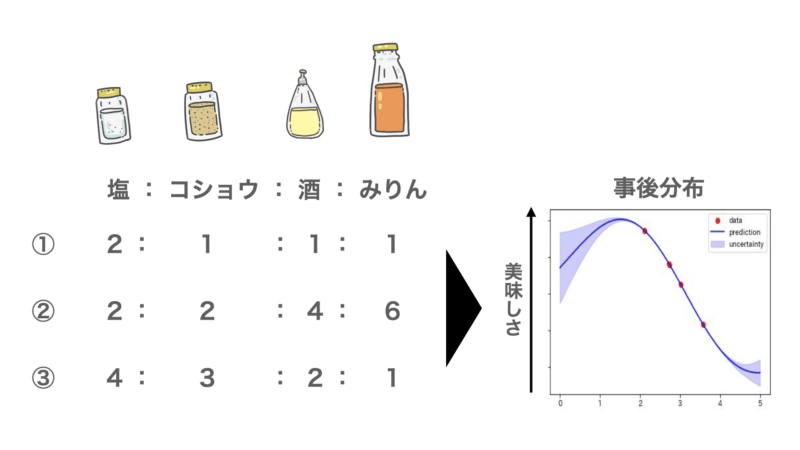
もう少し具体的に説明すると、事後分布はガウス過程回帰という手法を使用して計算しています。
ガウス過程回帰は評価指標の予測値とその分散を表現することができるため、目標値を達成する確率が高い組み合わせを見つけることができます。
詳細は以下の記事にまとめていますので参考にしていただければと思います。
4. 次のサンプル選択
事後分布を元に、次に試すレシピを選択します。美味しさが高そうなレシピや、未知の組み合わせを含むレシピを優先的に選択して試します。
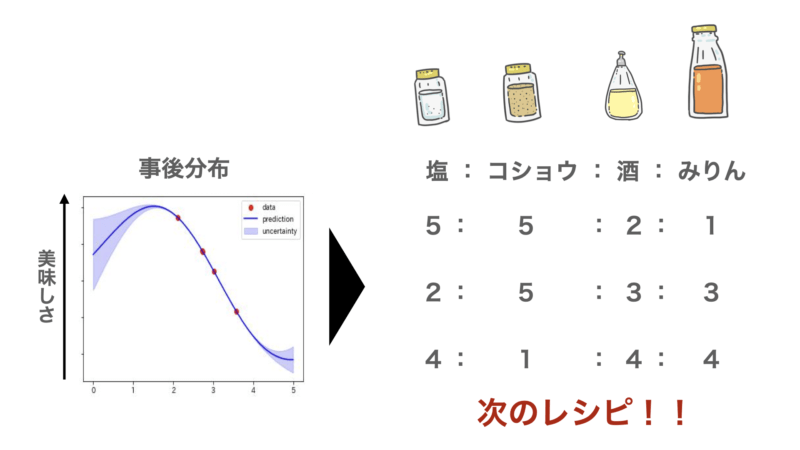

レシピの選択手法について具体的に説明すると獲得関数というものを使用して美味しくなるような次のレシピを選択します。詳しくは以下の記事に書いてありますので、興味のある方はご参照ください。
5. 反復
ステップ2からステップ4を繰り返し、美味しいと予想されるレシピで試行錯誤を続けます。これにより、少ない試食回数で美味しいレシピを見つける確率が高まります。
以上がざっくりとしたベイズ最適化のプロセスとなります。ざっくりとしたイメージを掴んでいただければ幸いです。
より実践的な内容としてPythonプログラムを使用したベイズ最適化について以下の記事にまとめていますので、よければ参考にしていただければと思います。
オススメの書籍
最後に、獲得関数やベイズ最適化についてさらに深く学びたい方に向けて、オススメの書籍をご紹介します。
ご紹介する
『Pythonで学ぶ実験計画法入門 ベイズ最適化によるデータ解析』
は、特に材料開発やプロセス開発における実験計画法に焦点を当てた、非常に実践的な内容となっています。
本書の特徴として
- ベイズ最適化の基本概念の解説
- 獲得関数やガウス過程回帰の詳細な解説
- 実際に使えるPythonコードとデータセットをGitHubからダウンロード可能
という点から、実際に手を動かしながらベイズ最適化を学ぶことができ理解がぐっと深まります。
特に、材料やプロセスの最適化を効率的に進めたいと考えている方には、本書のアプローチは非常に実用的で、すぐに現場に活かせる内容だと感じました。
さらに、ベイズ最適化以外にも、機械学習を活用したデータ解析手法について幅広く解説されているため、実験設計からデータ解析まで一貫して学びたい方にもぴったりです。
材料開発の現場で、データを最大限に活用したいと考えている方に、ぜひ手に取っていただきたい一冊です。
ベイズ最適化のオススメ参考書については以下の記事でもまとめていますので、興味のある方はご参照いただければと思います。
終わりに
ベイズ最適化は非常に便利な手法ではありますが、初めて勉強する方にとっては少しとっつきづらい気がします。そんな方に少しでもイメージを掴んでいただけたら幸いです。
もう少し詳細な数式などを勉強したい方は参考書を読むことをオススメします!