【初心者向け】ガウス過程回帰をわかりやすく説明〜Pythonで実装してみた〜

こんにちは！ぼりたそです！今回はベイズ最適化でも使用されるガウス過程回帰について初学者の方に向けてわかりやすく説明した記事になります。

この記事は以下の点をまとめています

Point

ガウス過程回帰とは？
　
ガウス過程回帰のメリット、デメリット
　
ガウス過程回帰のプロセス
　
Pythonで実行
　
オススメの書籍

それではガウス過程回帰についてご説明していきます。

ガウス過程回帰（Gaussian Process Regression, GPR）とは？
なぜガウス過程回帰（GPR）が必要なのか？
ガウス過程回帰のアルゴリズム
ガウス過程回帰をPythonで実行
オススメの書籍
終わりに

ガウス過程回帰（Gaussian Process Regression, GPR）とは？

みなさんは、こんな課題に直面したことはないでしょうか？

予測だけでなく「その予測がどれくらい信用できるか」という情報も知りたい

こうした課題に非常に有効なのが、ガウス過程回帰（Gaussian Process Regression, GPR） です。

GPRは、単に入力と出力の関係を予測するだけではなく、その予測の不確実性（どのくらいブレるか）も同時に計算できるという点で、他の回帰手法とは一線を画しています。

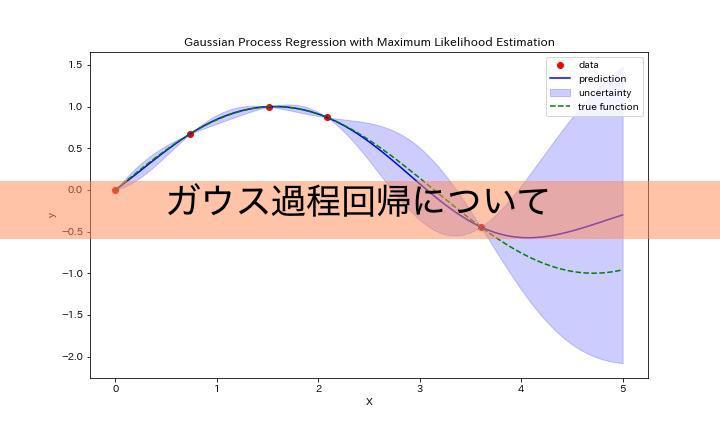
とはいえ、これだけだとあまりイメージが湧かないと思いますので、実際にガウス過程回帰をしたグラフを下に示します。

このグラフはy＝sin(x)に従う5点（赤点）を入力データとしてガウス過程回帰を実行した結果になります。緑の破線が真のグラフであるのに対して、青線が予測のグラフになっています。

さらに、青色で塗りつぶされているのが予測の分散になります。真のグラフに対してデータが少ない領域は分散が大きく、予測値も外れていることがわかりますね。

このように入力データに対して、予測値とその分散を出力できるのがガウス過程回帰になります

最近ではベイズ最適化においてガウス過程回帰の使用が増えており、実務や研究でも注目度が高まっています。

この記事では、GPRの概要、数式の意味、Pythonでの実装例、そして他の回帰手法との違いまで、
初学者の方にも分かりやすく順を追って説明していきます。

なぜガウス過程回帰（GPR）が必要なのか？

機械学習などでデータ予測を行う際、よく次のような課題に直面するかと思います。

課題1：データ数が少ない
→ 実験やシミュレーションのコストが高く、十分なデータが集められない場合が挙げられると思います。
例：材料開発、新薬探索、装置パラメータ調整など。
　
課題2：予測の「信用度」がわからない
→ 多くの回帰手法は予測値を返してくれますが、「その予測がどのくらい信用できるか」という不確実性を教えてはくれません。
　
課題3：未知領域の探索が難しい
→ 実験や探索の最適化には、「予測値が良さそうで、かつ不確実性が高い領域」を優先的に選ぶ戦略が重要です。

上記課題に対して、一般的な機械学習手法では「少ないデータ」「不確実性の推定」「効率的な探索」の課題を同時に解決することは中々難しいです。

例として「線形回帰」、「ランダムフォレスト」、「ニューラルネットワーク」について強みや上記課題の限界を下の表に示します。

手法	強み	上記課題への限界
線形回帰	解釈しやすい、計算が速い	非線形パターンを捉えにくい
ランダムフォレスト	非線形対応、精度が比較的高い	不確実性を定量化しづらい
ニューラルネットワーク	複雑なパターンを学習可能	大量のデータが必要

これらに対してガウス過程回帰（GPR）は、次のような点で優位性があります。

少数データでも安定した予測と不確実性推定が可能
→ カーネル関数によって事前に「関数の形状」についての仮定を入れることで、データが少なくても過度にブレずに予測ができます。ただし、精度はカーネル選択やデータ特性に依存し、必ずしも他手法を上回るとは限りません。
　
予測値と同時に不確実性を提供
→ GPRは各予測点の標準偏差を出力するため、「この予測はどれくらい信用できるか」を把握できます。
　
未知領域の探索・最適化に強い
→ 「予測値」と「不確実性」を組み合わせて次の候補点を決める戦略に最適です（ベイズ最適化）。

これらの理由から、GPRは多くの応用分野で重要な役割を果たしています。以下では、そのアルゴリズムや実装例を詳しく見ていきましょう。

ガウス過程回帰のアルゴリズム

GPRが実際にどのような手順で予測を行っているのか、アルゴリズムに焦点を当てて解説します。
数式の説明を挟みながら、全体像を順を追って理解できるように進めていきます。

例として以下のような訓練データを使ってGPRを実行するとします。

$$X = [x_1, x_2, \dots, x_n], \quad y = [y_1, y_2, \dots, y_n]$$

この時GPRから得られる関数は以下のように表すことができます。

$$f(x) \sim GP(m(x), k(x, x’))$$

$ m(x) $は平均関数であり、$ k(x, x’) $はカーネル関数を表します。カーネル関数については後ほど説明いたします。

これに対し、GPRは以下のステップで実行していきます。

カーネル関数の選択
　
共分散行列の計算
　
予測分布の計算
ハイパーパラメータの最適化
　
予測結果の出力

カーネル関数の選択

まずは、「データどうしの似ている度合いを測るルール」を決めます。
これがカーネル関数です。

代表的なカーネルには以下のようなものがあります：

RBFカーネル（ガウスカーネル）

$$k(x, x’) = \exp\left(-\frac{|x – x’|^2}{2l^2}\right)$$

距離が近いデータは類似度が高く、遠いデータは類似度が低くなるような関数です。
滑らかな関数として回帰したいときに使い、最もよく使われる汎用型のカーネル関数です。

Maternカーネル

$$k(x, x’) = \frac{2^{1-\nu}}{\Gamma(\nu)}\left(\frac{\sqrt{2\nu}|x – x’|}{l}\right)^\nu K_\nu\left(\frac{\sqrt{2\nu}|x – x’|}{l}\right)$$

RBFよりも荒い関数の表現が可能。滑らかさをパラメータ $\nu$ で調整でき、実験データや自然現象に使いやすい特徴があります。

線形カーネル

$$k(x, x’) = x^T x’$$

単純な線形関係を仮定する。線形回帰に近い振る舞いをし、シンプルな関係が支配的な場合に使用します。

カーネル関数を選ぶことで、「データの背後にある法則がどういうものか」をGPRモデルに教えてあげます。

カーネルについて以下の記事でまとめていますので、詳細が気になる方は参照いただければと思います。

合わせて読みたい

共分散行列の計算

選んだカーネル関数を使って、すべての訓練データ間の関係をまとめた共分散行列 $K$ を作ります。

$$K_{ij} = k(x_i, x_j)$$

例：$ n $個のデータ点がある場合の共分散行列

$$K =
\begin{bmatrix}
k(x_1, x_1) & k(x_1, x_2) & \cdots & k(x_1, x_n) \\
k(x_2, x_1) & k(x_2, x_2) & \cdots & k(x_2, x_n) \\
\vdots & \vdots & \ddots & \vdots \\
k(x_n, x_1) & k(x_n, x_2) & \cdots & k(x_n, x_n)
\end{bmatrix}
$$

この行列は、後の予測計算の基盤となります。

予測分布の計算

予測したい新しい入力 $x_*$ に対して、平均値とばらつきを計算します。

$$\mu_* = k_*^T (K + \sigma_n^2 I)^{-1} y$$

$$\sigma_*^2 = k(x_*, x_*) – k_*^T (K + \sigma_n^2 I)^{-1} k_*$$

$\mu_* $：予測値
$\sigma_*^2$：予測の不確実性（分散）

ここで $k_*$ は、訓練データと $x_*$ のカーネル値ベクトルです。

ハイパーパラメータの最適化

カーネル関数には細かい設定（例：データ間がどれくらい近いと「近い」とみなすか）が必要です。
これをハイパーパラメータといいます。

GPRでは、与えられたデータに対して最もよく説明できるようにハイパーパラメータを自動調整することが多いです。
詳細についてここでは述べませんが、具体的には最尤推定という手法がよく使用されます。

ハイパーパラメータ最適化について以下の記事をまとめているので、詳細が気になる方は参照ください。

合わせて読みたい

予測結果の出力

最後に、予測値とばらつきを可視化します。

平均予測値（$\mu_*$）→ 線グラフ
信頼区間（$\pm 1.96 \sigma_*$） → 予測線の周囲に帯を表示

これにより、どの領域が予測に自信があり、どの領域が不確実かを理解できます。

ガウス過程回帰をPythonで実行

それでは実際にPythonを使用してガウス過程回帰を実行してみましょう。

今回はy=sin(x)に従う5つのデータからガウス過程回帰を実行するコードをご紹介します。

このコードではカーネル関数はRBF、ハイパーパラメータの最適化は最尤推定から実行しています。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C

# 真の関数
def true_function(X):
    return np.sin(X).ravel()

# 一元のデータを作成
np.random.seed(1)
X = np.sort(5 * np.random.rand(5, 1), axis=0)
y = true_function(X)

# ガウス過程回帰モデルの構築（最尤推定を使用）
kernel = C(1.0, (1e-3, 1e3)) * RBF(1.0, (1e-2, 1e2))
gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10, optimizer=None)

# モデルの学習
gp.fit(X, y)

# 予測のための新しいデータ点を作成
x_pred = np.linspace(0, 5, 100)[:, np.newaxis]

# 予測値と予測の不確かさ（分散）を計算
y_pred, std_dev = gp.predict(x_pred, return_std=True)
lower_bound = y_pred - 1.96 * std_dev
upper_bound = y_pred + 1.96 * std_dev

# プロット
plt.figure(figsize=(10,6))
plt.scatter(X, y, c='r', label='data')
plt.plot(x_pred, y_pred, 'b', label='prediction')
plt.fill_between(x_pred[:, 0], lower_bound, upper_bound, alpha=0.2, color='blue',label='uncertainty')

# 真の関数をプロット
true_y = true_function(x_pred)
plt.plot(x_pred, true_y, 'g', label='true function', linestyle='dashed')

plt.xlabel('X')
plt.ylabel('y')
plt.title('Gaussian Process Regression with Maximum Likelihood Estimation')
plt.legend()
plt.show()

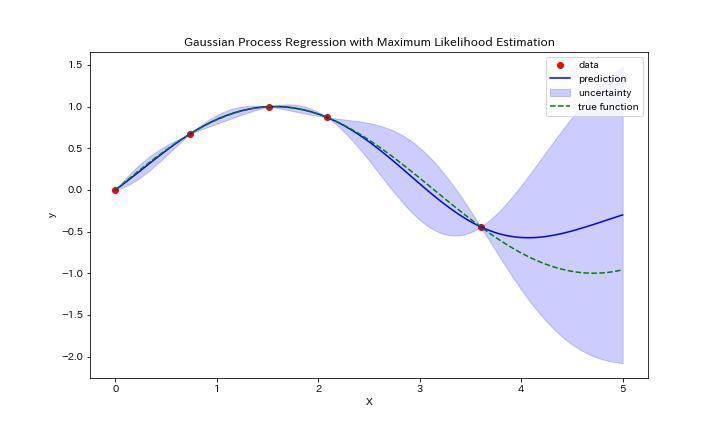
実際に得られたグラフがこちらになります。