こんにちは!ぼりたそです!
今回は「化合物の類似度を定量的に評価する方法」について、Python(RDKit)を用いた実装も交えてわかりやすくご紹介します。
この記事は以下のポイントでまとめています。
- なぜ化合物の類似度が必要なのか
- 類似度の計算手法
- Tanimoto係数
- Dice係数
- コサイン類似度
- ユークリッド距離
なぜ化合物の類似度が必要なのか
現在、世界中で発見されている化合物は2,000万種以上にのぼります。
これらの中には、構造的に似た化合物が数多く存在しており、創薬や材料開発においては、
- 有効成分に似た化合物を探索したい
- 構造が似ていると効果も似るのか検証したい
といった目的で「化学構造の類似度評価」が重要になります。
類似度の計算手法
化合物の類似度というと、ぱっと見た形や官能基の一致などを思い浮かべるかもしれません。
ですが、それでは主観が入りやすく、計算機によるスクリーニングには不向きです。
そこで本記事では、フィンガープリント(分子構造をビット列で表現したもの)を用いて定量的な手法で類似度を計算します。
これにより、定量的に構造を比較できるようになり、様々な類似度指標を計算できます。
詳しい仕組みやフィンガープリントの種類については、以下の記事もぜひご覧ください。
今回ご紹介する化合物の類似度評価手法については以下の通りとなります。
- Tanimoto係数
- コサイン類似度
- ユークリッド距離
- Dice係数
以下、順に解説していきます。
Tanimoto係数
まずはTanimoto係数についてご説明します。
Tanimoto係数は化合物の類似度評価においてはよく使用される手法になり、以下の式に従って算出されます。
$$\text{Tanimoto係数} = \frac{|A \cap B|}{|A| + |B| – |A \cap B|}$$
もう少し具体的に説明すると:
- $ |A| $ は、化合物 A のフィンガープリントにおいて 1 になっているビットの数。
- $ |B| $ は、化合物 B のフィンガープリントにおいて 1 になっているビットの数。
- $ |A \cap B| $ は、化合物 A と B の両方で 1 になっているビットの数。
仮に、以下のようなバイナリフィンガープリントを持つ化合物 A と B があるとします:
- 化合物 A のフィンガープリント: 101100
- 化合物 B のフィンガープリント: 110010
この場合、$|A| = 3$ 、 $|B| = 3$ 、$|A \cap B| = 2$となるので、
$$\text{Tanimoto係数} = \frac{|A \cap B|}{|A| + |B| – |A \cap B|} = \frac{2}{3 + 3 – 2} = \frac{2}{4} = 0.5$$
となります。
Tanimoto係数を使用する上でのメリット、デメリットは以下の通りです。
■メリット
■デメリット
それでは、実際にPythonで化合物のTanimoto係数を計算してみましょう。
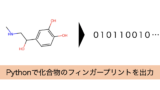
今回はベンゼンに対してトルエン、シクロヘキサン、n-ヘキサンのTanimoto係数を計算してみました。
実行コードは以下の通りです。
from rdkit import Chem
from rdkit.Chem import MACCSkeys, Draw
from rdkit.DataStructs import FingerprintSimilarity
# ベンゼン、トルエン、シクロヘキサン、ヘキサンのSMILES表現
smiles = {
'Benzene': 'c1ccccc1',
'Toluene': 'Cc1ccccc1',
'Cyclohexane': 'C1CCCCC1',
'Hexane': 'CCCCCC'
}
# 化合物の名前と分子を格納するリスト
molecules = [(name, Chem.MolFromSmiles(smile)) for name, smile in smiles.items()]
# ベンゼンの分子オブジェクトとMACCSフィンガープリント
benzene_fp = MACCSkeys.GenMACCSKeys(molecules[0][1])
# Tanimoto係数を計算する関数
def calculate_tanimoto(smiles, reference_fp):
mol = Chem.MolFromSmiles(smiles)
fp = MACCSkeys.GenMACCSKeys(mol)
return FingerprintSimilarity(reference_fp, fp)
# 各化合物のTanimoto係数を計算し、タイトルに追加
for i, (name, mol) in enumerate(molecules):
if name != 'Benzene':
similarity = calculate_tanimoto(smiles[name], benzene_fp)
molecules[i] = (f'{name}\nTanimoto: {similarity:.2f}', mol)
else:
molecules[i] = (f'{name}\nReference', mol)
# 分子を描画し、タイトルを追加
img = Draw.MolsToGridImage([mol for name, mol in molecules],
legends=[name for name, mol in molecules],
molsPerRow=4,
subImgSize=(300, 300))
結果を出力すると以下のように計算されていました。トルエン→シクロヘキサン→n-ヘキサンの順でTanimoto係数が大きく、類似していることになります。n-ヘキサンは0なので、全く似ていないという結果になっていますね。

Dice係数
次はDice係数について説明していきます。
Dice係数はTanimoto係数と似ていますが、少し計算手法が異なっており、共通の部分構造を持つ化合物同士を似ていると評価する傾向があります。Dice係数は以下の計算式から導かれます。
$$\text{Dice係数} = \frac{2 |A \cap B|}{|A| + |B|}$$
もう少し具体的に説明すると:
- $ |A| $ は、化合物 A のフィンガープリントにおいて 1 になっているビットの数。
- $ |B| $ は、化合物 B のフィンガープリントにおいて 1 になっているビットの数。
- $ |A \cap B| $ は、化合物 A と B の両方で 1 になっているビットの数。
仮に、以下のようなバイナリフィンガープリントを持つ化合物 A と B があるとします:
- 化合物 A のフィンガープリント: 101100
- 化合物 B のフィンガープリント: 110010
この場合、$|A| = 3$ 、 $|B| = 3$ 、$|A \cap B| = 2$となるので、
$$\text{Dice係数} = \frac{2 |A \cap B|}{|A| + |B|} = \frac{4}{3 + 3} = \frac{4}{6} = 0.66$$
となります。
Dice係数を使用する上でのメリット、デメリットは以下の通りです。
■メリット
■デメリット
それでは、Dice係数についてもPythonで類似度を評価していきます。
先ほどと同じようにベンゼンに対してトルエン、シクロヘキサン、n-ヘキサンについて計算していきます。
from rdkit import Chem
from rdkit.Chem import MACCSkeys, Draw
from rdkit.DataStructs import DiceSimilarity
from PIL import Image, ImageDraw
# ベンゼン、トルエン、シクロヘキサン、ヘキサンのSMILES表現
smiles = {
'Benzene': 'c1ccccc1',
'Toluene': 'Cc1ccccc1',
'Cyclohexane': 'C1CCCCC1',
'Hexane': 'CCCCCC'
}
# 化合物の名前と分子を格納するリスト
molecules = [(name, Chem.MolFromSmiles(smile)) for name, smile in smiles.items()]
# ベンゼンの分子オブジェクトとMACCSフィンガープリント
benzene_fp = MACCSkeys.GenMACCSKeys(molecules[0][1])
# Dice係数を計算する関数
def calculate_dice(smiles, reference_fp):
mol = Chem.MolFromSmiles(smiles)
fp = MACCSkeys.GenMACCSKeys(mol)
return DiceSimilarity(reference_fp, fp)
# 各化合物のDice係数を計算し、タイトルに追加
for i, (name, mol) in enumerate(molecules):
if name != 'Benzene':
similarity = calculate_dice(smiles[name], benzene_fp)
molecules[i] = (f'{name}\nDice: {similarity:.2f}', mol)
else:
molecules[i] = (f'{name}\nReference', mol)
# 分子を描画し、タイトルを追加
img = Draw.MolsToGridImage([mol for name, mol in molecules],
legends=[name for name, mol in molecules],
molsPerRow=4,
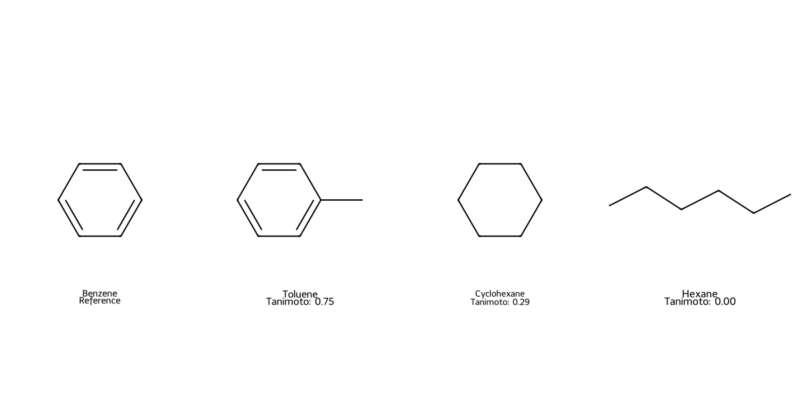
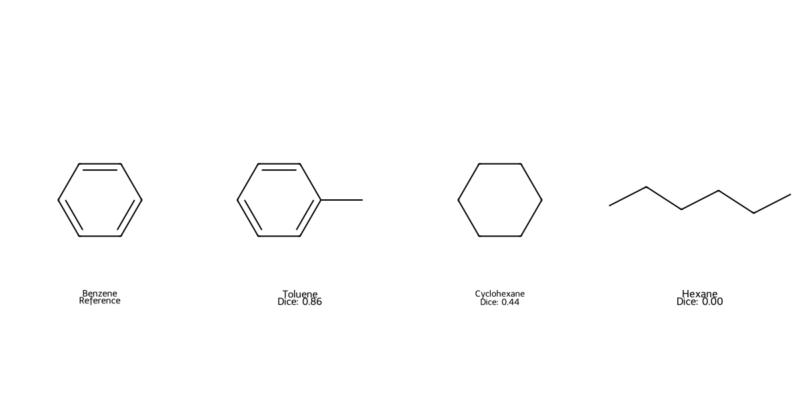
subImgSize=(300, 300))結果を出力してみると以下のように計算されており、Tanimoto係数と同様にトルエン→シクロヘキサン→n-ヘキサンの順に係数が大きく、類似している結果となっています。
Tanimoto係数よりも若干係数が大きく計算されており、共通構造が大きく評価されているようです。

コサイン類似度
次にコサイン類似度を紹介していきます。
コサイン類似度は以下の式より計算することができます。
$$\text{Cosine Similarity} = \frac{A \cdot B}{\lVert A \rVert \cdot \lVert B \rVert}$$
もう少し具体的に説明すると:
- $ \lVert A \rVert $ は、化合物 A のフィンガープリントにおけるノルム(ベクトルの大きさ)。
- $ \lVert B \rVert $ は、化合物 B のフィンガープリントにおけるノルム(ベクトルの大きさ)。
- $ A \cdot B $ は、化合物 A と B のフィンガープリントの内積。
仮に、以下のようなバイナリフィンガープリントを持つ化合物 A と B があるとします:
- 化合物 A のフィンガープリント: 10110100
- 化合物 B のフィンガープリント: 01010101
\begin{align*}
\text{内積} & : A \cdot B\\&
= (1 \times 0) + (0 \times 1) + (1 \times 0) + (1 \times 1) + (0 \times 0) + (1 \times 1) + (0 \times 0) + (0 \times 1) \\ & = 1 + 0 + 0 + 1 + 0 + 1 + 0 + 0 \\ & = 3 \\
\\
\text{ノルム} & : \lVert A \rVert\\&
= \sqrt{1^2 + 0^2 + 1^2 + 1^2 + 0^2 + 1^2 + 0^2 + 0^2} \\ & = \sqrt{4} = 2 \\ \text{ノルム} & : \lVert B \rVert\\&
= \sqrt{0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 1^2} \\ & = \sqrt{4} = 2 \\
\\
\text{コサイン類似度} & : \text{Cosine Similarity} = \frac{A \cdot B}{\lVert A \rVert \cdot \lVert B \rVert} \\ &
= \frac{3}{2 \times 2} = \frac{3}{4} = 0.75
\end{align*}
コサイン類似度を使用する上でのメリット、デメリットは以下の通りです。
■メリット
■デメリット
それではコサイン類似度についてもPythonを使用して化合物の類似度を評価していきます。
使用したコードは以下の通りです。
from rdkit import Chem
from rdkit.Chem import AllChem, Draw
from rdkit.DataStructs import FingerprintSimilarity
# ベンゼン、トルエン、シクロヘキサン、n-ヘキサンのSMILES表現
smiles = {
'Benzene': 'c1ccccc1',
'Toluene': 'Cc1ccccc1',
'Cyclohexane': 'C1CCCCC1',
'n-Hexane': 'CCCCCC'
}
# 化合物の名前と分子を格納するリスト
molecules = [(name, Chem.MolFromSmiles(smile)) for name, smile in smiles.items()]
# ベンゼンのフィンガープリント
benzene_fp = AllChem.GetMorganFingerprintAsBitVect(molecules[0][1], 2)
# コサイン類似度を計算する関数
def calculate_cosine_similarity(fp1, fp2):
return FingerprintSimilarity(fp1, fp2)
# 各化合物のコサイン類似度を計算し、表示
for i, (name, mol) in enumerate(molecules):
if name != 'Benzene':
fp = AllChem.GetMorganFingerprintAsBitVect(mol, 2)
similarity = calculate_cosine_similarity(benzene_fp, fp)
molecules[i] = (f'{name}\nCosine Similarity: {similarity:.2f}', mol)
else:
molecules[i] = (f'{name}\nReference', mol)
# 分子を描画し、タイトルを追加
img = Draw.MolsToGridImage([mol for name, mol in molecules],
legends=[name for name, mol in molecules],
molsPerRow=4,
subImgSize=(300, 300))
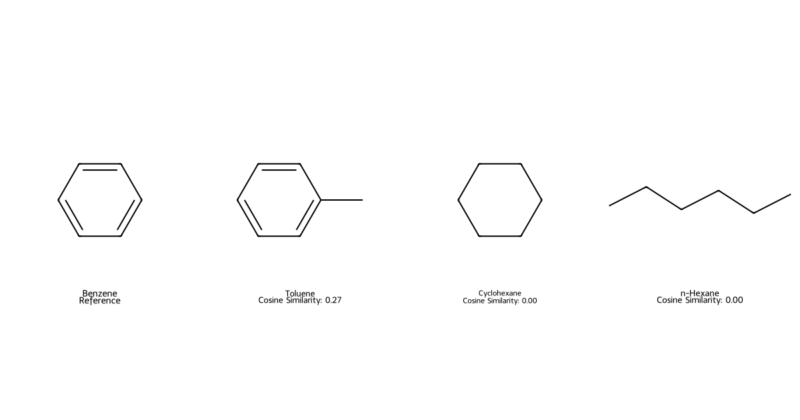
結果を出力すると以下の通りとなり、Tanimoto係数やDice係数と異なり、係数が大分小さくなっていることがわかります。コサイン類似度はフィンガープリントのベクトル同士の角度が小さいほど類似していると判断するので、フィンガープリントが長いほど値が小さくなる傾向にあるかもしれません。

ユークリッド距離
最後にユークリッド距離についてご紹介します。
ユークリッド距離は、多次元空間内の2つの点間の距離を測るための一般的な方法の1つです。化合物の類似度を評価するために使用されることがあります。ユークリッド距離は、2つの点 $P = (p_1, p_2, p_3, \ldots, p_n)$ と $Q = (q_1, q_2, q_3, \ldots, q_n)$ の間の距離を次の式で計算します:
$$\sqrt{(p_1 – q_1)^2 + (p_2 – q_2)^2 + \ldots + (p_n – q_n)^2}$$
化合物の場合、類似度はユークリッド距離が小さいほど類似していると見なされます。
ユークリッド距離を使用する上でのメリット、デメリットは以下の通りです。
■メリット
■デメリット
ユークリッド距離についてもPythonで化合物の類似度を評価してみました。
実際のコードは以下の通りです。
from rdkit import Chem
from rdkit.Chem import AllChem
import numpy as np
# ベンゼン、トルエン、シクロヘキサン、n-ヘキサンのSMILES表現
smiles = {
'Benzene': 'c1ccccc1',
'Toluene': 'Cc1ccccc1',
'Cyclohexane': 'C1CCCCC1',
'n-Hexane': 'CCCCCC'
}
# 化合物の名前と分子を格納するリスト
molecules = [(name, Chem.MolFromSmiles(smile)) for name, smile in smiles.items()]
# ベンゼンのフィンガープリント
benzene_fp = AllChem.GetMorganFingerprintAsBitVect(molecules[0][1], 2)
# ユークリッド距離を計算する関数
def calculate_euclidean_distance(fp1, fp2):
v1 = np.asarray(fp1)
v2 = np.asarray(fp2)
return np.linalg.norm(v1 - v2)
# 各化合物のユークリッド距離を計算し、表示
for i, (name, mol) in enumerate(molecules):
if name != 'Benzene':
fp = AllChem.GetMorganFingerprintAsBitVect(mol, 2)
similarity = calculate_euclidean_distance(benzene_fp, fp)
molecules[i] = (f'{name}\nEuclidean distance: {similarity:.2f}', mol)
else:
molecules[i] = (f'{name}\nReference', mol)
# 分子を描画し、タイトルを追加
img = Draw.MolsToGridImage([mol for name, mol in molecules],
legends=[name for name, mol in molecules],
molsPerRow=4,
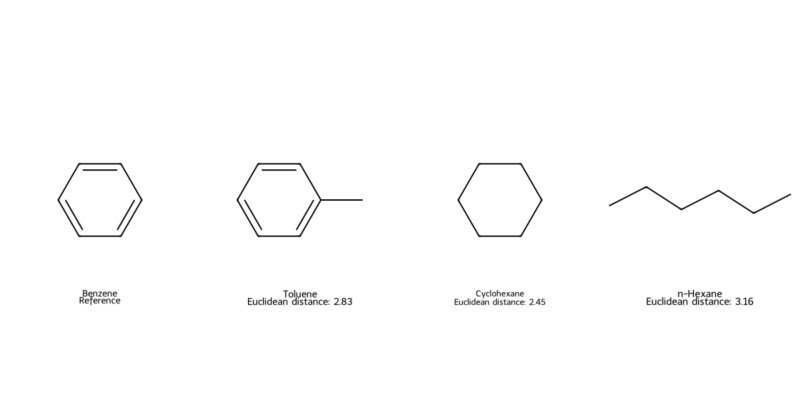
subImgSize=(300, 300))結果を出力すると以下のようにシクロヘキサン→トルエン→n-ヘキサンの順にユークリッド距離が小さくなり類似度が高いことがわかります。他の評価手法と異なり、トルエンよりもシクロヘキサンの類似度の方が高く計算されていますね。
ユークリッド距離は単純なフィンガープリントベクトルの2点間距離を計算しているだけなので、違った結果になるのでしょう。

終わりに
以上がフィンガープリントを使用した化合物の類似度評価手法になります。本記事で紹介した方法以外にも評価手法は存在しており、それぞれで指標が異なるため、目的に合わせて評価指標を選択することが重要になってきます。他の評価方法についてはお時間があればまた紹介していきたいと思います。